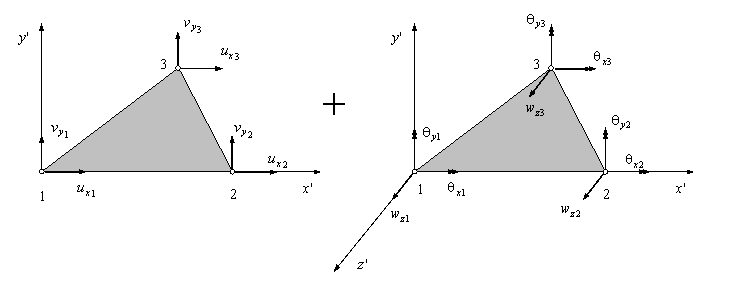
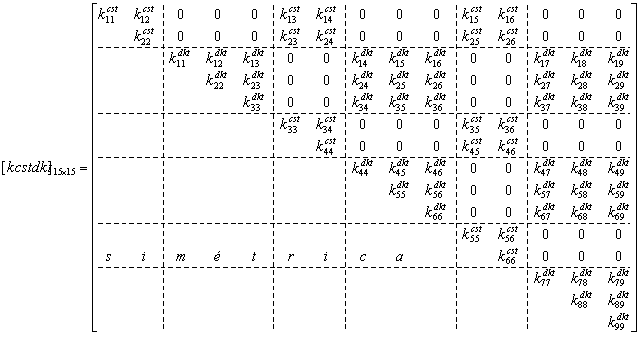
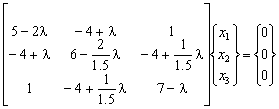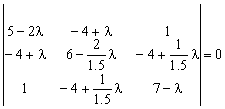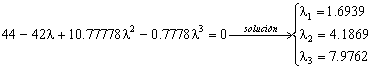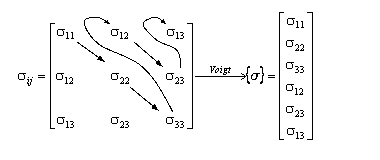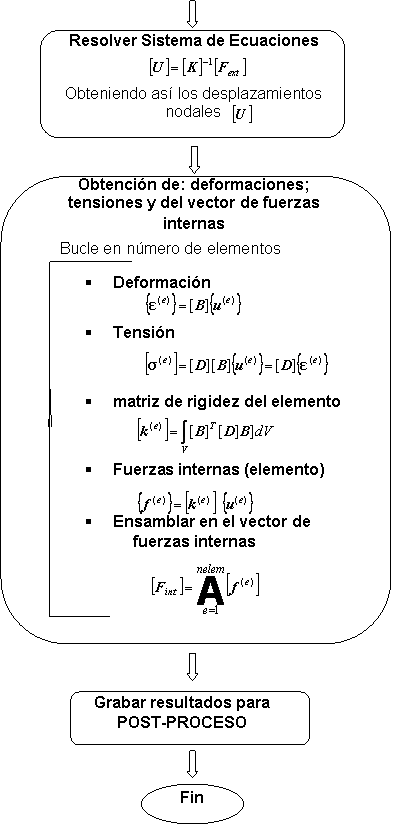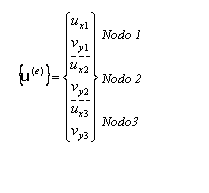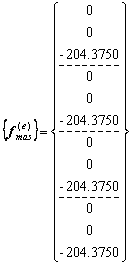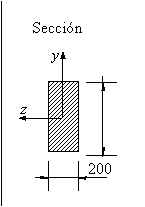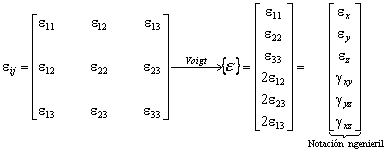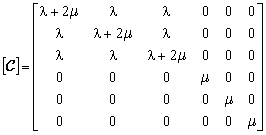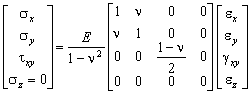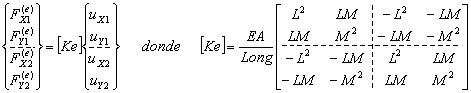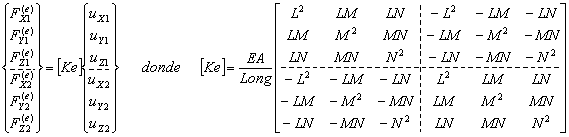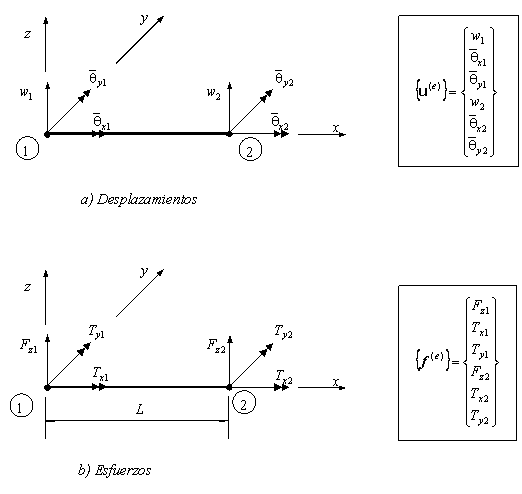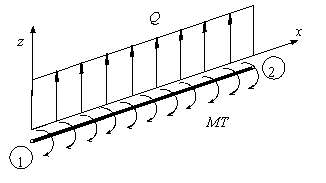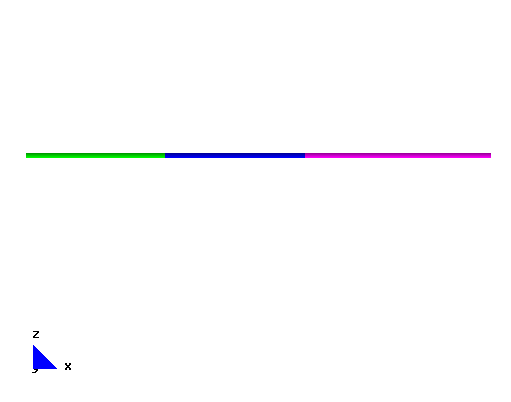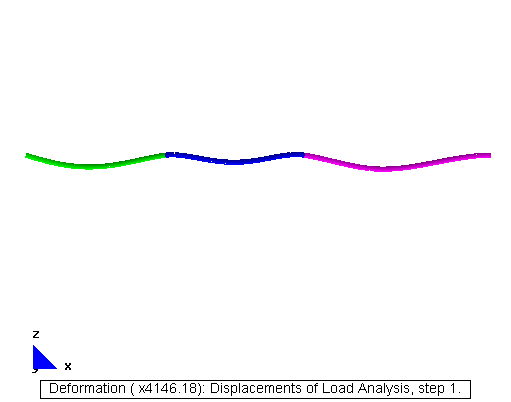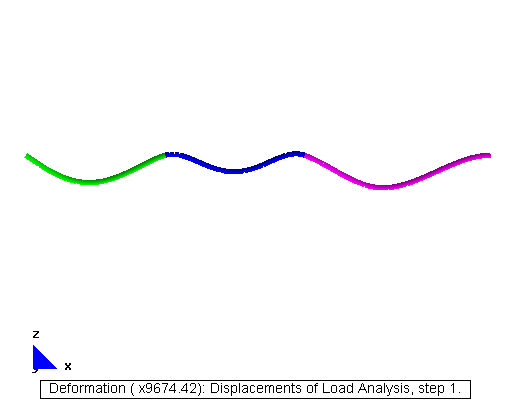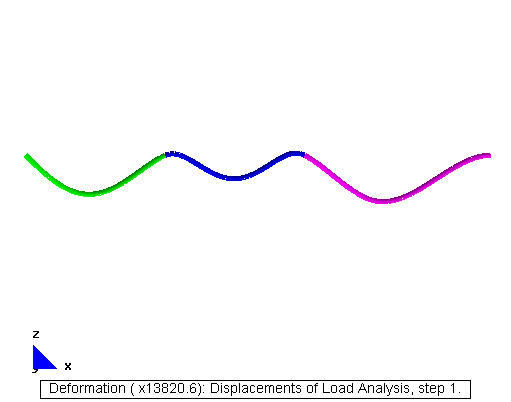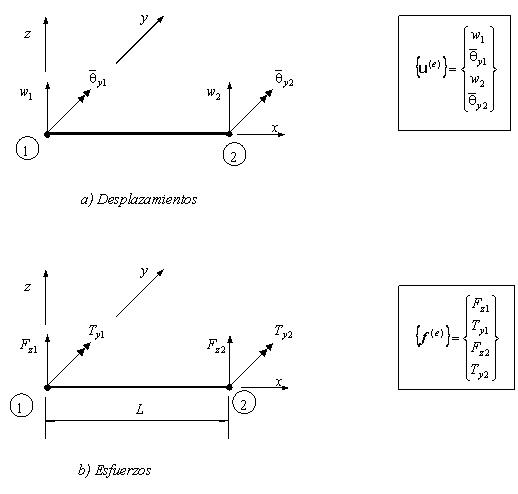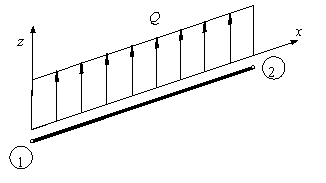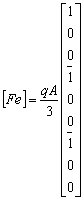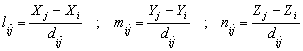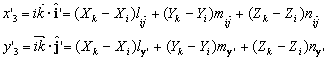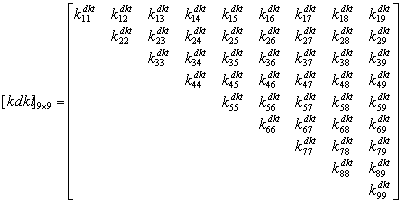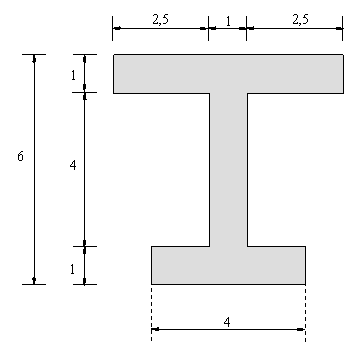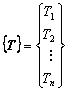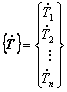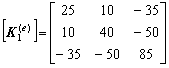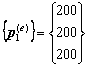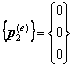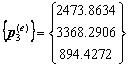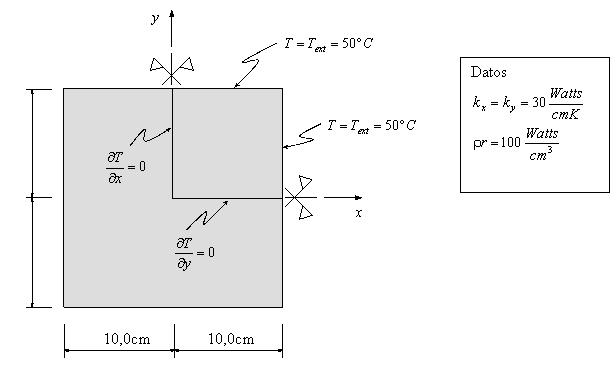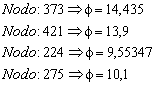Presentación
Bibliografía
E.W.V.Chaves & R. Mínguez (2009). Mecánica Computacional en la Ingeniería con Aplicaciones en MATLAB
Herramientas Auxiliares
Configuración del Developer Studio
Tiempo de execución
SUBROUTINE CPUTIM(RTIME)
Esta subrutina proporciona el tiempo de ejecución del programa en segundos.
Post_Proceso – GID
Problem Type
Problem_type_vigas.gid.rar (basado en Problem_type_solid2)
Herramientas matemáticas I
Operaciones con Vectores
SUBROUTINE VECASI(N,V1,V2)
SUBROUTINE LVECAS(N,V1,V2)
SUBROUTINE VECUNI(N,V,MODUL)
Obtiene el versor según la dirección de ![]() .
.
![]() , donde
, donde ![]() es el módulo del vector
es el módulo del vector ![]()
SUBROUTINE VECDOT(V1,V2,N,VDOT)
Producto escalar entre los vectores ![]() y
y ![]()
SUBROUTINE VECPRO(V1,V2,V3)
Producto vectorial entre los vectores ![]() ,
, ![]() y almacena en
y almacena en ![]()
SUBROUTINE VECSCA(N,A,V1,V2)
![]() , donde
, donde ![]() es una constante real.
es una constante real.
SUBROUTINE VECADD(N,V1,V2,V3)
SUBROUTINE LVECAD(N,V1,V2,V3)
SUBROUTINE VECUPD(N,A,V1,V2)
![]() , donde
, donde ![]() es una constante real.
es una constante real.
SUBROUTINE VECDIF(N,V1,V2,V3)
SUBROUTINE VECCOM(N,A,B,V1,V2,V3)
![]() , donde
, donde ![]() ,
, ![]() son constantes reales
son constantes reales
SUBROUTINE VECBAS(V1,V2,V3)
Dado un vector ![]() , esta subrutina obtiene una base ortonormal:
, esta subrutina obtiene una base ortonormal:
Operaciones con Matrices
SUBROUTINE MATASI(N1,V1,N2,V2)
SUBROUTINE TRANSP(FMATX,NDIME)
SUBROUTINE PROMA1(A,B,C,N1,N2,N3)
SUBROUTINE MATMB(A,B,V,NX)
Esta subrutina obtiene la siguiente operación entre matrices:
Datos de entrada A,B,NX
Salida: A
SUBROUTINE PROMA2(A,B,C,N1,N2,N3)
SUBROUTINE PROMA3(A,B,C,N1,N2,N3)
SUBROUTINE BTAB3(A,B,V,NX)
Esta subrutina obtiene la siguiente operación entre matrices:
Datos de entrada A,B,NX
Salida: A
Determinantes de Matrices
SUBROUTINE DETERM(A,DETER,N)
Herramientas Auxiliares
SUBROUTINE VECZER(N,V)
SUBROUTINE LVECZE(N,V)
Herramientas matemáticas II
Autovalor y Autovector
SUBROUTINE VECVAL(A,B,H,V,ERR,NX)
Proporciona los autovalores y autovectores del siguiente sistema de ecuaciones:
![]() . y
. y ![]() es el error utilizado en la subrutina de JACOB.
es el error utilizado en la subrutina de JACOB.
Variables de entrada A,B,ERR,NX. Valores auxiliares H,V
Salida: Autovalores están en la diagonal principal de la matriz A. Autovectores están en la matriz B.
En el caso clásico de autovalor ![]() la matriz es la matriz identidad.
la matriz es la matriz identidad.
Depende de las siguiente subrutinas: DECOG, INVCH, BTAB3, JACOB, MATMB
Salida: Autovalores ![]() (autovalores en la diagonal principal), Autovectores
(autovalores en la diagonal principal), Autovectores ![]() .
.
Ejemplo
Consideremos el siguiente sistema de ecuaciones:
Podemos reestructurar las expresiones anteriores en forma matricial como:
La solución analítica (exacta) sigue a continuación, para ello reestructuramos la expresión anterior como:
Este sistema de ecuaciones homogéneo solo tiene solución no trivial si y solo si:
Desarrollando el determinante obtenemos que:
[/vc_column_text][/vc_tta_section][vc_tta_section title=»Herramientas matemáticas III» tab_id=»1547466790804-5b16881e-4748″][vc_column_text]
Transformación de Base
SUBROUTINE TRANS6(B,T,IFLA1,IFLA2)
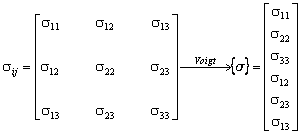
Esta subrutina construye la matriz de transformación para un tensor de segundo orden cuando éste esté en la notación de Voigt.
Matriz de transformación de base:
Notación de Voight que se considera:
Ley de transformación de base de un tensor de segundo orden en notación de Voigt:
donde
Para el caso:
Tenemos que:
Siendo válido que:
Herramientas Geométricas
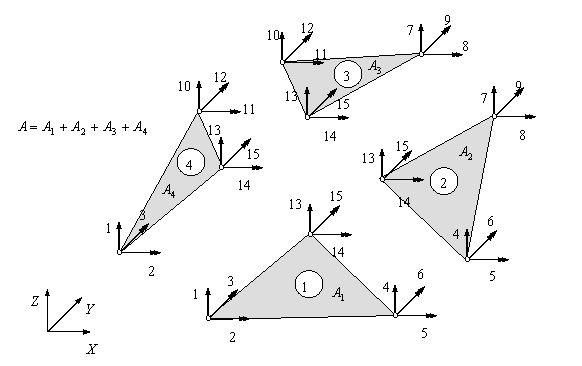
SUBROUTINE AREATR3D (X,Y,Z,VEC,AREA)
Cálculo de área de un triángulo, utilizando la definición del producto vectorial:
Input: Coordenadas nodales X(3),Y(3),Z(3)
Output: AREA (Área del elemento triangular; VEC(3) (vector unitario normal al elemento de área)
SUBROUTINE AREATR2D(X,Y,AREA)
Input: Coordenadas nodales X(3),Y(3)
Output: AREA (Área del elemento triangular)
SUBROUTINE LONGB (X,Y,Z,LONG,L,M,N)
Esta subrutina retorna la longitud entre dos puntos.
Input: Coordenadas X(2),Y(2),Z(2)
Output: LONG (Longitud), L,M,N (cosenos directores)
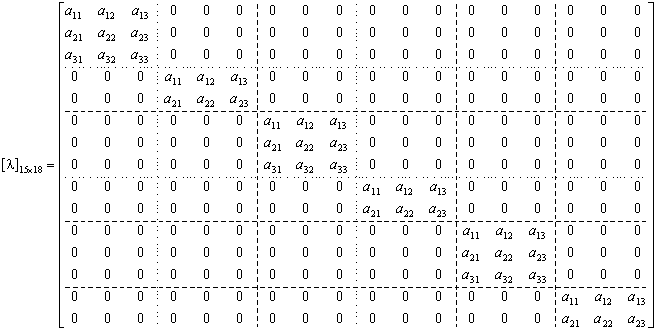
Resolución de Sistema de Ecuaciones
Resolución del Sistema Almacenado en Banda
SUBROUTINE SOLVERBAND (N,LBAND,RB,U)
Esta subrutina resuleve el sistema ![]() .
.
En esta subrutina ![]() está almacenada en banda tal y como se indica en la figura abajo:
está almacenada en banda tal y como se indica en la figura abajo:
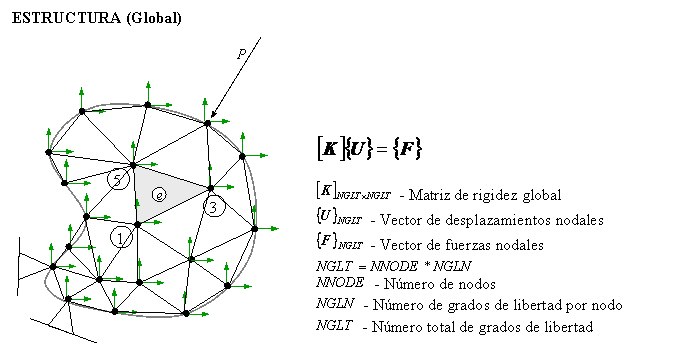
donde ![]() es el número de grados de libertad por nodo,
es el número de grados de libertad por nodo, ![]() es la diferencia máxima de la numeración nodal de los elementos.
es la diferencia máxima de la numeración nodal de los elementos.
Ejemplo:
Subroutina para calcular el ancho de banda
Resolución del Sistema (Matriz no necesariamente simétrica)
SUBROUTINE SOLVER1 (NV,R,U)
Esta subrutina resuelve el sistema ![]()
Integracion_Num. y Diferencias finitass
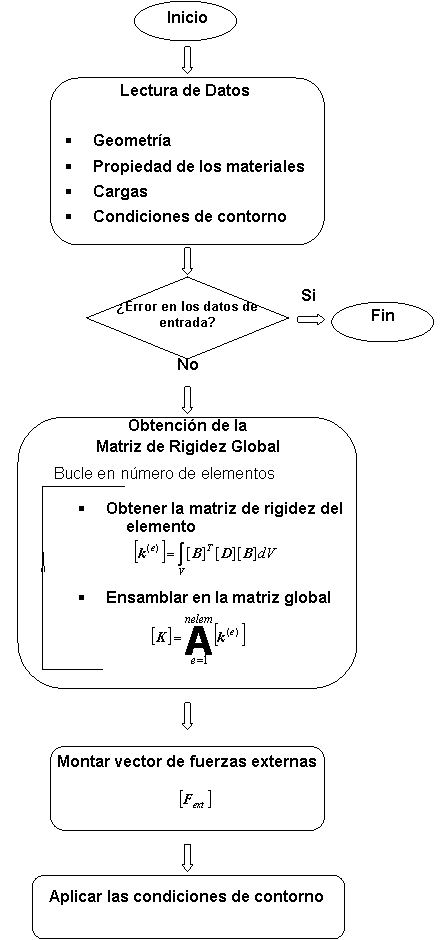
Diagrama de Flujo del MEF
A continuación se presenta la estructura de un diagrama de flujo de un programa basado en el método de los elementos finitos para un problema elástico lineal.
FLUJO
ENSAMBLAJE
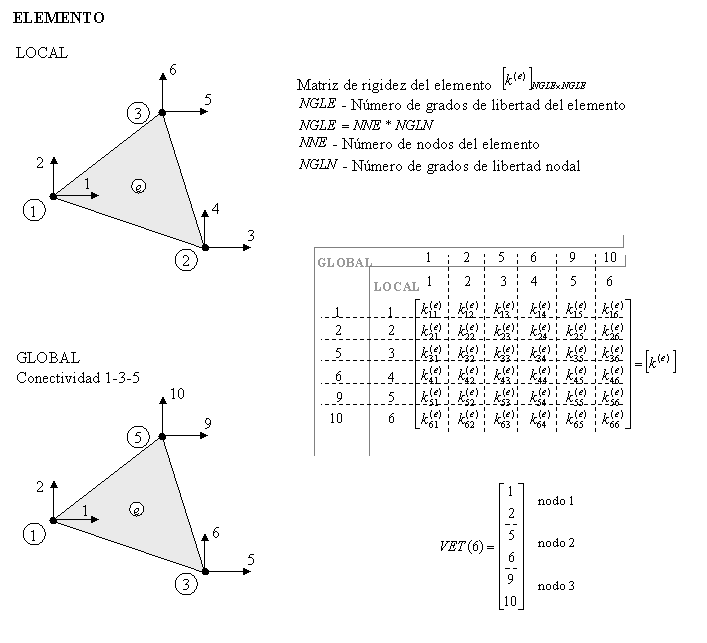
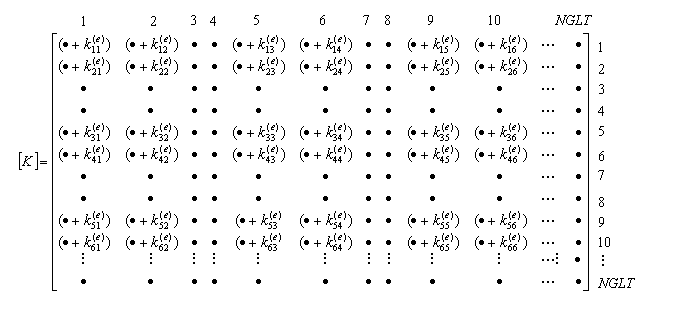
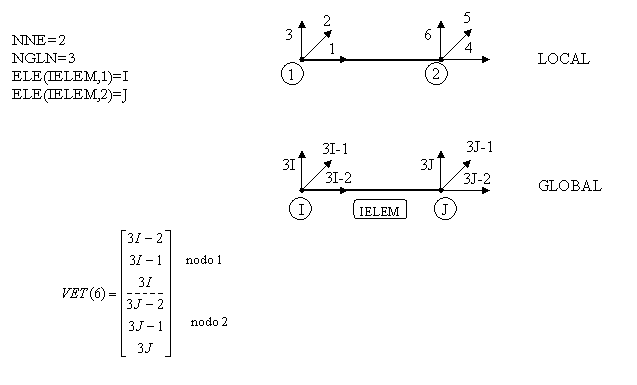
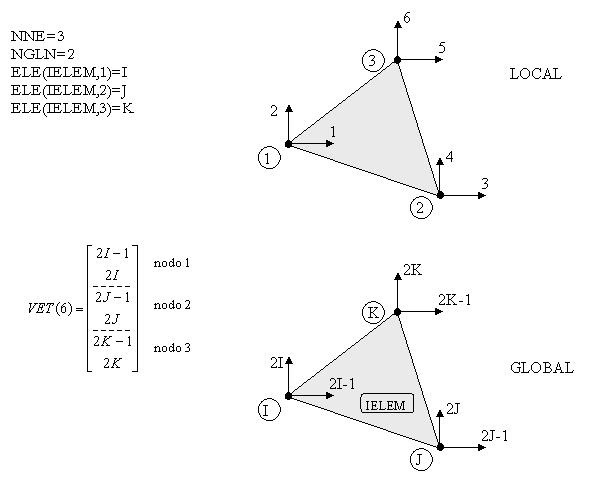
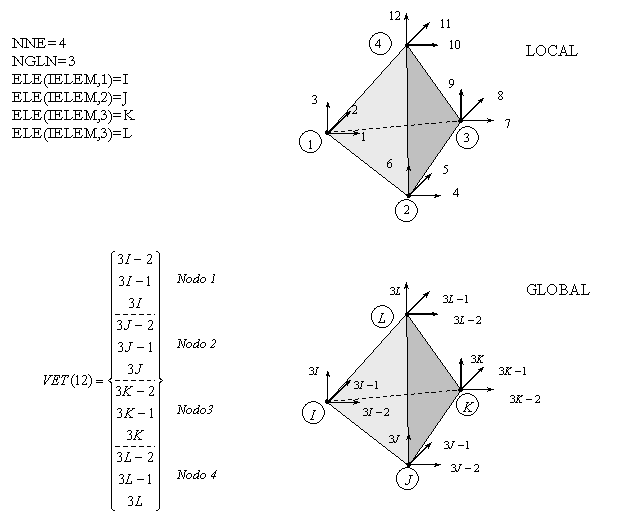
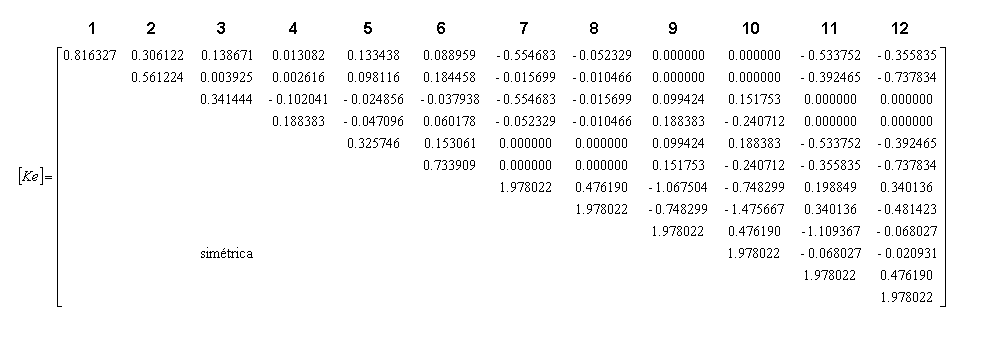
Práctica – Construcción del la Matriz de Rigidez Global
Contribución de la matriz de rigidez del elemento ![]() en la matriz de rigidez global
en la matriz de rigidez global ![]()
Práctica: Hacer un procedimiento para la construcción de la matriz de rigidez. Utilizar alocación dinámica para definir las variables relacionadas con el elemento, e.g. KE(NGLE,NGLE), P_MAT(NPAR), XC(NNE,NDIME), etc.
ENSAMBLAJE- Vector Auxiliar
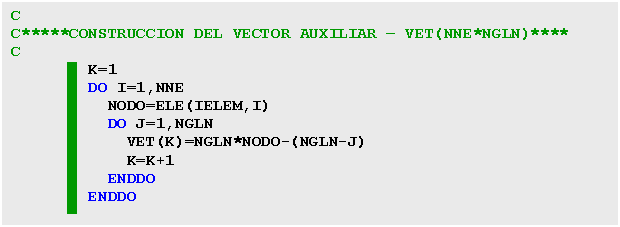
Práctica – Construcción del Vector Auxiliar VET
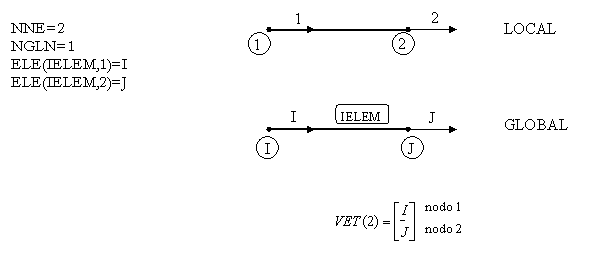
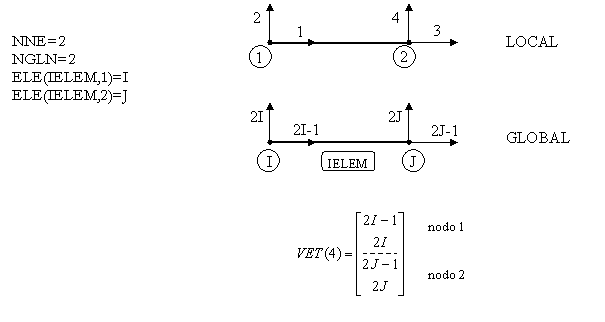
Práctica
Construir un vector VET genérico tal que relacione la numeración local con la numeración global, donde hay que tener en cuenta los siguientes datos de entrada:
INPUT (todas variables tipo INTEGER):
NNE – Número de nodos del elemento
NGLN – Número de grados de libertad del nodo
ELE(NELEM,NNE) – Conectividad del elemento
NELEM – Número de elementos
IELEM – Número del elemento para la obtención de VET
OUTPUT(todas variables tipo INTEGER):
VET(NNE*NGLN)
A continuación se muestran unos ejemplos y el formato que presenta el vector VET.
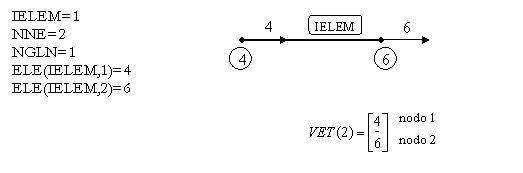
Ej. 1
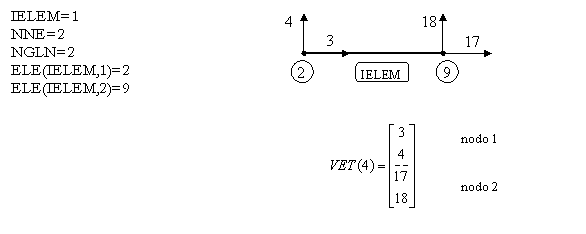
Ej. 2
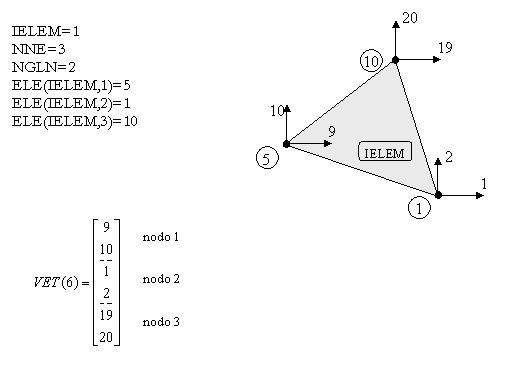
Ej. 3
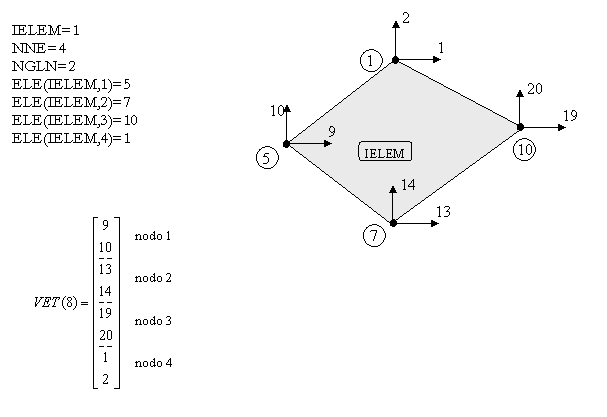
Ej. 4
Ej. 5
SOLUCIÓN
Procedimiento para la construcción del vector VET:
Implementar el procedimiento y verificar si se cumple para los siguientes casos particulares:
Ejemplo 1
Ejemplo 2
Ejemplo 3
Ejemplo 4
Elasticidad Lineal
Elasticidad Plana-2D
CST-Triángulo con Deformación Constante LST-Triángulo con Deformación Lineal Cuadrilatero
CST-Triángulo con Deformación Constante
Subrutinas para la obtención de la matriz de rigidez y del vector de fuerzas del elemento CST. El vector de desplazamientos nodales viene almacenado como:
SUBRUTINAS AUXILIARES
LISTEN.F – LECTURA DE DATOS
GID_POST.F – POST-PROCESO
MATRIZ DE RIGIDEZ
SUBROUTINE STIFCST(XC,E,POI,T,EST,KE)
Esta subrutina obtiene la matriz de rigidez explícita del elemento finito CST.
Input: EST=1 – Estado de Tensión Plana, EST=2 – Estado de Deformación Plana, T-espesor; E- Módulo de Young, POI-Poisson, XC(3,2) – Coordenadas de los nodos del elemento
Output: Ke(6,6) – Matriz de rigidez ![]()
Subrutinas Auxiliares: MATD_2D.F AREATR2D.F
OTRA FORMA PARA LA OBTENCIÓN DEL CST
SUBROUTINE STIFCST_N(XC,E,POI,T,EST,KE)
Esta subrutina obtiene la matriz de rigidez numéricamente del elemento finito CST.
Input: EST=1 – Estado de Tensión Plana, EST=2 – Estado de Deformación Plana, T-espesor; E- Módulo de Young, POI-Poisson, XC(3,2) – Coordenadas de los nodos del elemento
Output: Ke(6,6) – Matriz de rigidez ![]()
Subrutinas Auxiliares: MATD_2D.F AREATR2D.F; MATB_CST.F; BDBCO1.F
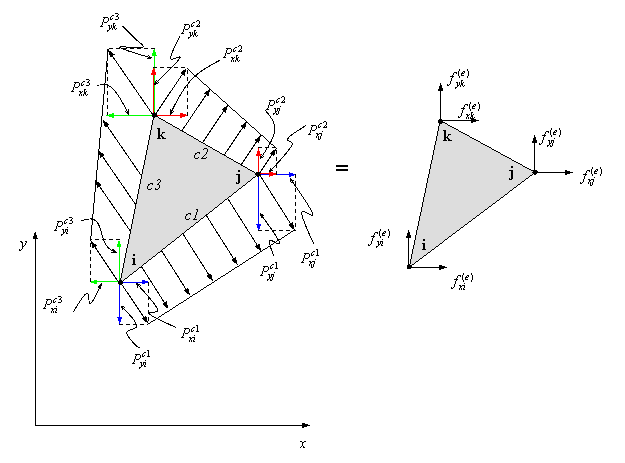
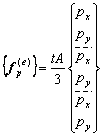
VECTOR DE FUERZAS NODALES – CST
Fuerzas Nodales debido a Deformaciones Iniciales (Variación de Temperatura)
SUBROUTINE TEMCST(EST,XC,T,YOUNG,POI,ALFA,DT,FE_THE)
Esta subrutina obtiene el vector de fuerzas nodales debido a deformaciones iniciales producidas por la variación de temperatura .
Input: Propiedades geométricas: t-espesor;
Propiedades mecánica: ![]() -módulo de Young,
-módulo de Young, ![]() – coeficiente de Poisson
– coeficiente de Poisson
Propiedades térmicas: ![]() -coeficiente de dilatación térmica,
-coeficiente de dilatación térmica, ![]() – variación de la temperatura.
– variación de la temperatura.
Si Estado de Tensión Plana:
Si Estado de Deformación Plana
OBS.: Errata, página 209, ecuación 5.69
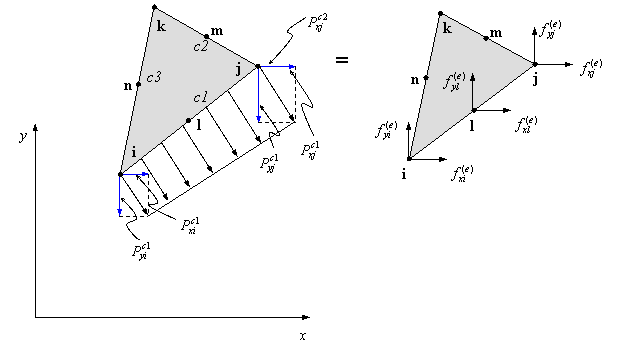
Fuerzas Nodales debido a Fuerzas de superficies
SUBROUTINE SURCST(XC,T,P_FOR,FE_SUP)
Esta subrutina obtiene el vector de fuerzas nodales debido a la fuerza de superficie aplicada en la cara del elemento.
donde
Fuerzas Nodales debido a Fuerzas Másicas (Ver pg. 207)
SUBROUTINE MASCST(XC,T,DENSI,NX,NY,GRAVITY,FE_MAS)
El vector ![]() tiene por unidad en el SI:
tiene por unidad en el SI: ![]() .
.
Subrutinas Auxiliares: AREATR2D.F
LST-Triángulo con Deformación Lineal
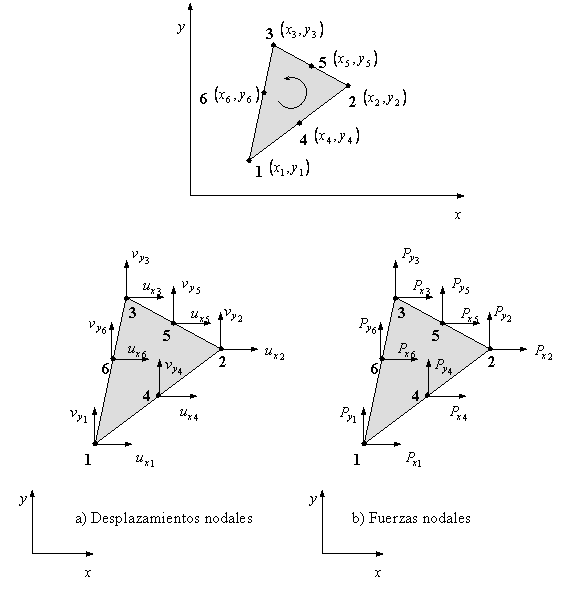
Las subrutinas a continuación son válidas para elemento triangular de 6 nodos (con los lados rectos. El vector de desplazamientos del elemento tiene el formato:
SUBRUTINAS AUXILIARES
LISTEN.F – LECTURA DE DATOS
GID_POST.F – POST-PROCESO
MATRIZ DE RIGIDEZ -LST
SUBROUTINE STIFLST (XC,E,POI,T,EST,KE)
Esta subrutina obtiene la matriz de rigidez explícita para el elemento finito LST.
Input: XC(6,2)- Coordenadas de los nodos, E-módulo de Young, POI-coeficiente de Poisson, T-espesor, EST=1- Estado de Tensión Plana; EST=2-Estado de Deformación Plana.
Output: Ke(12,12) – Matriz de rigidez ![]()
Subrutinas Auxiliares: AREATR2D.F
OTRAS FORMAS PARA LA OBTENCIÓN DEL ELEMENTO LST
SUBROUTINE STIFLST2 (XC,E,POI,T,EST,KE)
Subrutinas auxiliares: AREATR2D.F; MATD_2D.F
NUMÉRICAMENTE
SUBROUTINE STIFLST3 (XC,E,POI,T,EST,KE)
Subrutinas Auxiliares: MATD_2D.F AREATR2D.F; MATBLST.F; BDBCO1.F
EJEMPLO
MATRIZ DE RIGIDEZ
VECTOR DE FUERZAS NODALES -LST
FUERZAS MÁSICAS
FUERZAS DE SUPERFICIE
Pre-proceso:
Conectividad del elemento: i-j-k-l-m-n
Conectividad de la cara : i-j-l
Conectividad de la cara : j-k-m
Conectividad de la cara : k-i-n
FUERZAS NODALES DEBIDO A LA VARIACIÓN DE TEMPERATURA
| Tensión Plana | Deformación Plana |
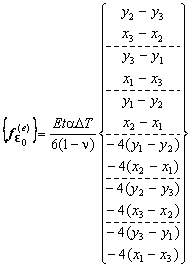 |
 |
Cuadriláteros
SUBRUTINAS AUXILIARES
LISTEN.F – LECTURA DE DATOS
GID_POST.F – POST-PROCESO
MATRIZ DE RIGIDEZ – CUADRILÁTEROS 4-NODOS
CUADRILÁTERO REGULAR
SUBROUTINE STIFCS4(EST,T,E,POI,X,Y,KE)
Esta subrutina obtiene la matriz de rigidez del elemento finito rectangular de 4 nodos.
Input: EST=1- Estado de Tensión Plana; EST=2-Estado de Deformación Plana, T-espesor, E-módulo de Young, POI-coeficiente de Poisson, X(4),Y(4)- Coordenadas de los nodos.
Output: Ke(8,8) – Matriz de rigidez ![]()
Subrutina auxiliar: MATD_2D.F
MATRIZ DE RIGIDEZ DEL CUADRILÁTERO 4 NODOS
Integración Numérica
SUBROUTINE STIFCS4N(EST,T,E,POI,X,Y,KE)
Subrutinas auxiliares: MATD_2D.F, MATBCS4.f, BDBCO1.f
VECTOR DE FUERZAS NODALES
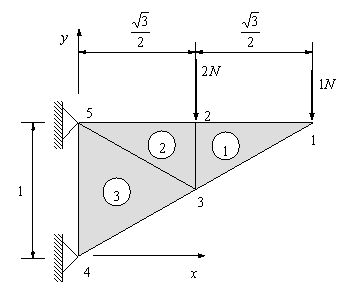
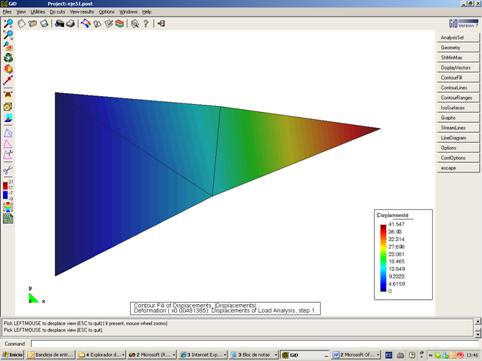
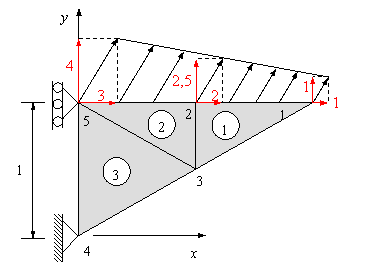
Ejercicio de Elasticidad Plana-CST
Ejemplo Ilustrativo 5.1 (pg.215)
Fichero de entrada: EJE51.DAT
Formato de los ficheros del post-proceso (GID)
Ejemplo Ilustrativo (fuerza de superficie)
Mismo ejemplo que el anterior, pero cambiando las cargas y condiciones de contorno.
Vector de fuerzas nodales:
Fichero de entrada: EJE_TRACTION.DAT
Formato de los ficheros del post-proceso (GID)
Ejemplo Ilustrativo (Variación de Temperatura) – Tensiones Iniciales
Vector de fuerzas nodales:
Fichero de entrada: EJE_TEPERATURE.DAT
Formato de los ficheros del post-proceso (GID)
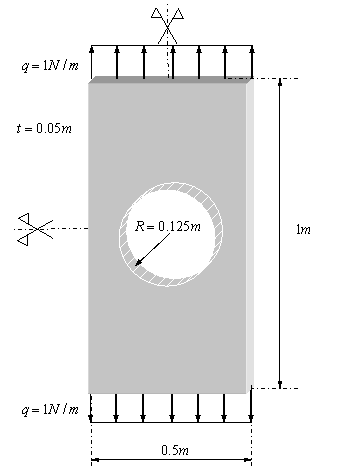
Ejemplo PLACA AGUJEREADA (pg.240)
Fichero de entrada: PLACA_AGUJ.DAT
Ejemplo VIGA (pg.240)
Fichero de entrada: VIGA1.DAT
Ejemplo con Variación de Temperatura
Ejemplo 1: Sin tensión, con deformación
Fichero de datos: Termico2.dat
Ejemplo 2: Sin deformación, con tensión
Fichero de datos: Termico3.dat
[/vc_column_text][vc_column_text]Soy un bloque de texto. Haz clic en el botón Editar para cambiar este texto. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Ejemplo Elasticidad Plana 2D- LST
Ejercicio de Elasticidad Plana – LST
Ejemplo Académico – Fuerza de superficie
Fichero de entrada: SURFACE6N.DAT
Estado de tensión plana
Vector de Fuerzas Nodales
Formato de los ficheros del post-proceso (GID)
Ejemplo Académico – Variación de Temperatura
Misma geometría y condiciones de contorno que el ejemplo anterior, cambiando solamente la acción. Ahora el material está sometido a un cambio de temperatura de . Considerando un Estado de Deformación Plana.
Fichero de entrada: TEMPERATURA_6N.DAT
Formato de los ficheros del post-proceso (GID)
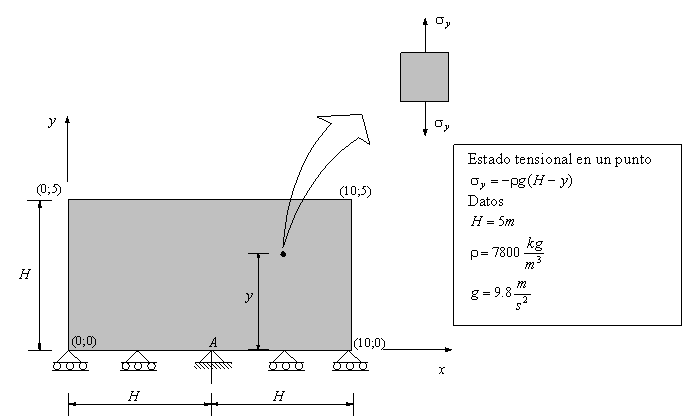
Ejemplo Académico 2 – Peso propio
Estado de tensión plana.
Para el punto el estado tensional queda: (compresión)
Discretización de elementos finitos
Campo de Tensiones – Componente
Fichero de entrada: PESO_PROPIO4.DAT
Formato de los ficheros del post-proceso (GID)
Ejercicio 1
Hacer el mismo ejemplo académico 2 utilizando el elemento CST y utilizar distintas mallas de elementos finitos (con distintos grados de refinamiento) y verificar convergencia.
Ejercicio 2
Hacer el mismo ejemplo académico 2 cambiando las condiciones de contorno para que tenga en cuenta que el terreno esté confinado.
Ejercicio de Elasticidad Bidimensional – 2D
Ejercicio de Elasticidad Bidimensional – 2D
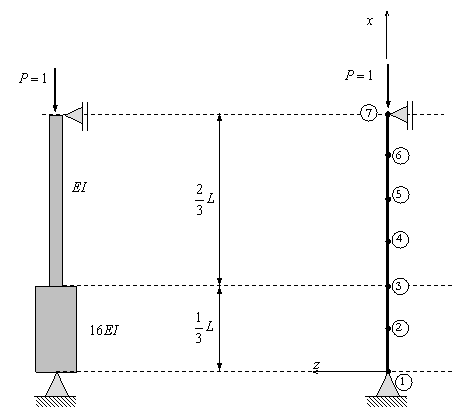
Ejemplo de Sensibilidad de la Malla
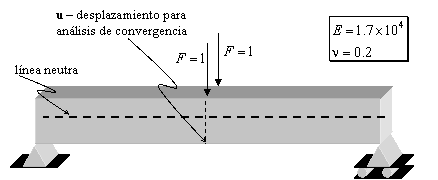
CONSIDERANDO LA HIPÓTESIS DE TEORÍA DE VIGAS
Deflexión de la línea neutra en el centro (ver ejemplo de Vigas):
Momento de Inercia:
Diagrama de Cortante
Diagrama de Flector (positivo si tracciona fibra inferior)
MÉTODO DE LOS ELEMENTOS FINITOS
Condiciones de apoyo
Mallas
(LST) viga00_L.dat
(CST) viga1_C.dat – (LST) viga1_L.dat
(CST) viga2_C.dat – (LST) viga2_L.dat
(CST) viga3_C.dat – (LST) viga3_L.dat
Cuadriláteros
Análisis de la sección A-A (Caso Viga3_L.dat) (LST)
Desplazamiento X
Como podemos ver, según la gráfica abajo, la sección A-A que era plana antes de la deformada, tras la deformada sigue siendo plana.
Tensión en la sección A-A
Podemos aproximar la curva anterior a una parábola cuya área es
Luego el cortante actuante en la sección A-A es .
Según la teoría de vigas, el cortante en esta sección es igual a .
ANÁLISIS DE LA SECCIÓN B-B
Luego el momento en la sección es:
VIGA DE GRAN CANTO
Vamos considerar una viga de gran canto. Para ello consideramos el ejemplo anterior y solo cambiando el ancho de la viga que en lugar de 0,5m será igual a 6m.
Tras la deformada vemos que la sección A-A que era plana deja de ser plana. Violando así la hipótesis fundamental para considerar una viga a través de la teoría de vigas.
Deformada
[/vc_column_text][/vc_tta_section][vc_tta_section i_icon_fontawesome=»fa fa-sitemap» add_icon=»true» title=»Elasticidad Tridimensional-3D» tab_id=»1623062671191-22e79782-b4e9″][vc_column_text]
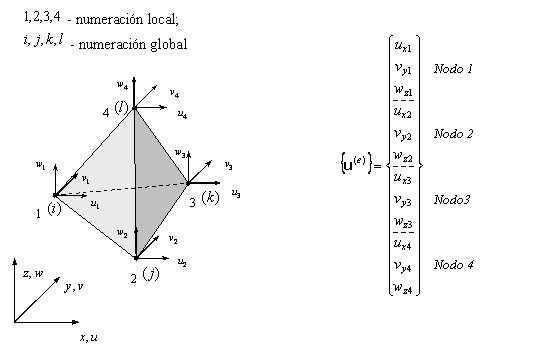
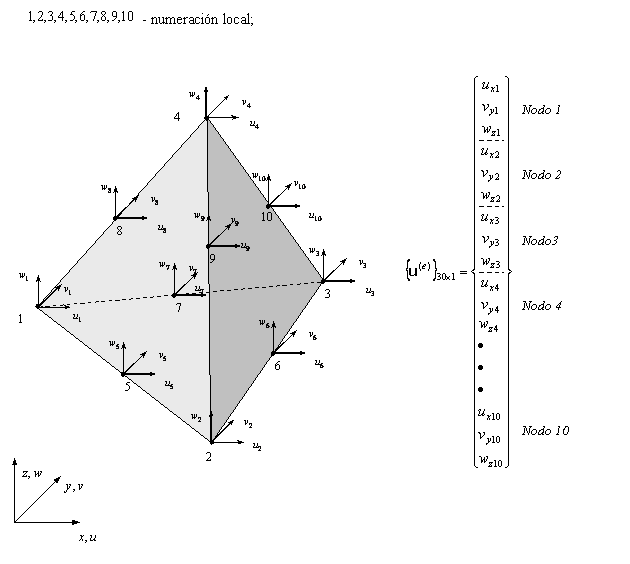
Tetraedro – 4 Nodos Tetraedro – 10 Nodos Hexaedro – 8 Nodos
Tetraedro – 4 Nodos
Subrutinas para la obtención de la matriz de rigidez y del vector de fuerzas del elemento tetraédrico de 4 nodos. El vector de desplazamientos nodales viene almacenado como:
Conectividad adoptada para los nodos de las caras: El vector área de las caras tiene sentido hacia dentro del elemento. Por ejemplo, el vector resultante: ![]() apunta hacia dentro del elemento. Luego, la conectividad de la cara
apunta hacia dentro del elemento. Luego, la conectividad de la cara ![]() será
será ![]() , también puede tener las siguientes conectividades:
, también puede tener las siguientes conectividades: ![]() , verificando que el vector resultante:
, verificando que el vector resultante: ![]() apunta hacia dentro del elemento, o aun
apunta hacia dentro del elemento, o aun ![]() . Lo mismo para las restantes caras..
. Lo mismo para las restantes caras..
SUBRUTINAS AUXILIARES
LISTEN.F – LECTURA DE DATOS
GID_POST.F – POST-PROCESO
MATRIZ DE RIGIDEZ
Opción 1
SUBROUTINE STIFT4NT(XC,YOUNG,POI,KE)
Esta subrutina obtiene la matriz de rigidez del elemento tetraédrico de 4 nodos.
Input: XC(4,3) – Coordenadas de los nodos del elemento; YOUNG- Módulo de Elasticidad Longitudinal, POI-Poisson,
Output: Ke(12,12) – Matriz de rigidez
Subrutinas Auxiliares: MATB4NTN.F; MATD_3D; BDBCO1.F.
Opción 2 – Numéricamente
SUBROUTINE STIFT4NN(XC,YOUNG,POI,KE)
Esta subrutina obtiene la matriz de rigidez del elemento tetraédrico de 4 nodos utilizando integración numérica.
Input: XC(4,3) – Coordenadas de los nodos del elemento; YOUNG- Módulo de Elasticidad Longitudinal, POI-Poisson,
Output: Ke(12,12) – Matriz de rigidez
Subrutinas Auxiliares: MATB4NTN.F; MATD_3D; BDBCO1.F; RUTOPE.F; SHAPE3.
VECTOR DE FUERZAS NODALES – Tetraedro 4 Nodos
Fuerzas Nodales debido a Deformaciones Iniciales (Variación de Temperatura)
SUBROUTINE TEM4NT(EST,XC,YOUNG,POI,ALFA,DT,FE_THE)
Esta subrutina obtiene el vector de fuerzas nodales debido a deformaciones iniciales producidas por la variación de temperatura para materiales isótropos .
Input: Propiedades geométricas: t-espesor;
Propiedades mecánica: ![]() -módulo de Young (YOUNG),
-módulo de Young (YOUNG), ![]() – coeficiente de Poisson (POI)
– coeficiente de Poisson (POI)
Propiedades térmicas: ![]() -coeficiente de dilatación térmica (ALFA),
-coeficiente de dilatación térmica (ALFA), ![]() – variación de la temperatura (DT).
– variación de la temperatura (DT).
donde ![]() es la matriz que contiene las derivadas de las funciones de forma del elemento tetraedro de 4 nodos.
es la matriz que contiene las derivadas de las funciones de forma del elemento tetraedro de 4 nodos.
Subrutinas Auxiliares: MATB4NT.F.
Fuerzas Nodales debido a Fuerzas de superficies (ver página 250)
SUBROUTINE SUR4NT(XC,TIPO,P_FOR,FE_SUP)
Fuerzas Nodales debido a Fuerzas Másicas (ver pg. 249)
SUBROUTINE MAS4NT(XC,DENSI,NX,NY,NZ,GRAVITY,FE_MAS)
El vector ![]() tiene por unidad en el SI:
tiene por unidad en el SI: ![]() .
.
donde ![]() es el volumen del elemento.
es el volumen del elemento.
Subrutinas Auxiliares: DETERM.F
Tetraedro – 10 Nodos
Subrutinas para la obtención de la matriz de rigidez y del vector de fuerzas del elemento tetraédrico de 10 Nodos. El vector de desplazamientos nodales viene almacenado como:
SUBRUTINAS AUXILIARES
LISTEN.F – LECTURA DE DATOS
GID_POST.F – POST-PROCESO
MATRIZ DE RIGIDEZ
SUBROUTINE STIFT10NN(XC,YOUNG,POI,KE)
Esta subrutina obtiene la matriz de rigidez del elemento tetraédrico de 10 nodos utilizando integración numérica.
Input: XC(10,3) – Coordenadas de los nodos del elemento; YOUNG- Módulo de Elasticidad Longitudinal, POI-Coeficiente de Poisson.
Input: Ke(30,30) – Matriz de rigidez.
Subrutinas Auxiliares: MATB4NTN.F; MATD_3D; BDBCO1.F; RUTOPE.F; SHAPE3.
VECTOR DE FUERZAS NODALEST
FUERZAS MÁSICAS
FUERZAS DE SUPERFICIE
FUERZAS NODALES DEBIDO A LA VARIACIÓN DE TEMPERATURA
Hexaedro – 8 Nodos
SUBRUTINAS AUXILIARES
LISTEN.F – LECTURA DE DATOS
GID_POST.F – POST-PROCESO
MATRIZ DE RIGIDEZ
VECTOR DE FUERZAS NODALES
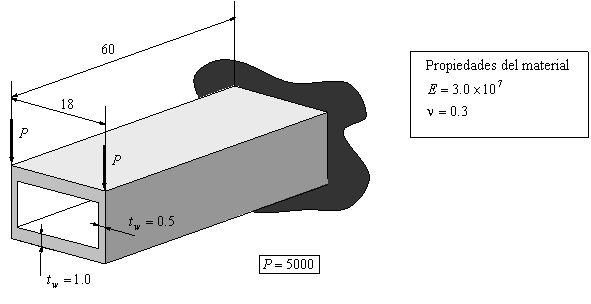
![]() [/vc_column_text][/vc_tta_section][vc_tta_section title=»Ejercicio de Elasticidad – 3D» tab_id=»1547813326718-3fbe24d8-1ef7″][vc_column_text]Ejemplo Ilustrativo 5.2 (pg.246)
[/vc_column_text][/vc_tta_section][vc_tta_section title=»Ejercicio de Elasticidad – 3D» tab_id=»1547813326718-3fbe24d8-1ef7″][vc_column_text]Ejemplo Ilustrativo 5.2 (pg.246)
Fichero de entrada: ELAST3D1.DAT
Formato de los ficheros del post-proceso (GID)
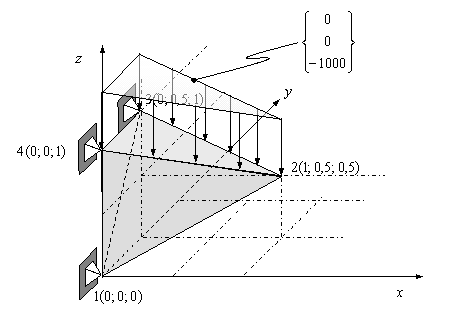
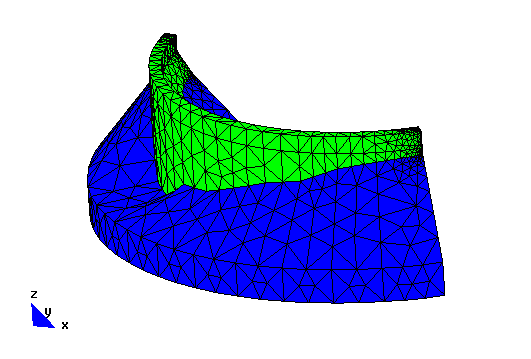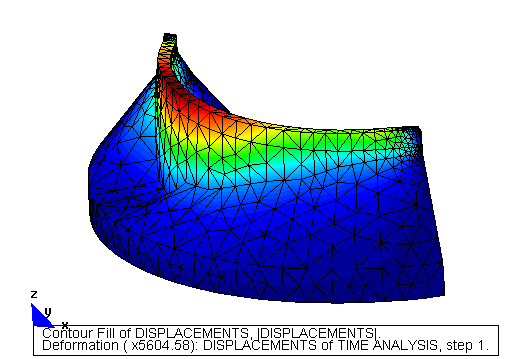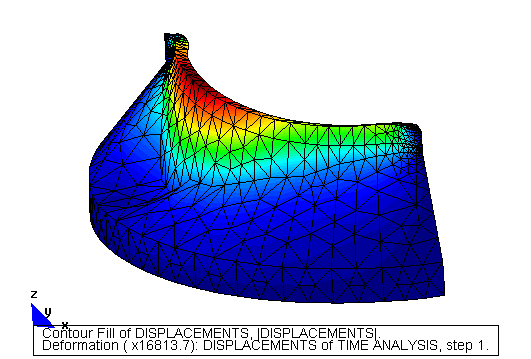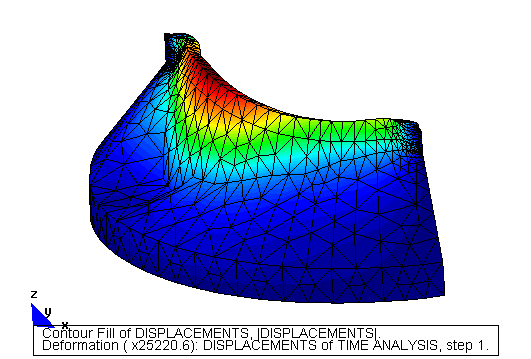
Ejemplo Ilustrativo (fuerza de superficie+peso propio)
Fichero de datos: ELAST3D1G.DAT
Este ejemplo tiene las mismas coordenadas que el anterior, cambiando únicamente las cargas. Una fuerza de superficie tal (global) y como se indica en la figura. También se considerara el peso propio cuya densidad será considerada igual a ![]() y la aceleración de la gravedad igual a:
y la aceleración de la gravedad igual a: ![]() .
.
Área de la cara (324): ![]() y el volumen del tetraedro es igual a:
y el volumen del tetraedro es igual a: ![]() .
.
Vector de fuerzas nodales debido a la fuerza de superficie:
Vector de fuerzas nodales debido al peso propio:
Vector total de fuerzas nodales:
Ejemplo Académico (fuerza de superficie (local)+peso propio)
Fichero de datos: BLOQUE.DAT
Formato de los ficheros del post-proceso (GID)
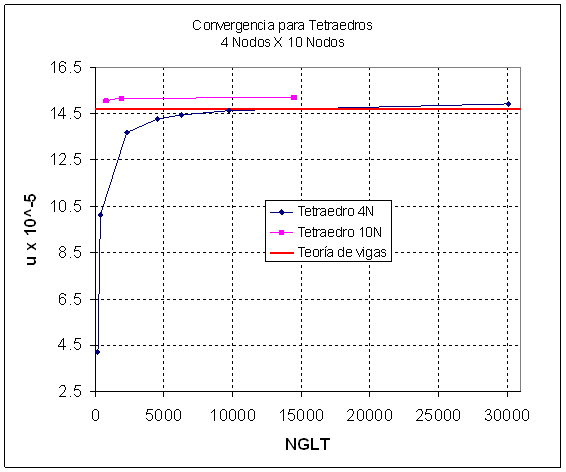
Ejemplo de Sensibilidad de la Malla
Sección transversal
Teoría de vigas: Deflexión de la línea neutra en el centro:
Malla 1 – 56 nodos, 93 elementos Tetra4nodos, NGLT=168: ( BEAM1_T4.DAT)
Malla 1 – 266 nodos, 99 elementos, Tetra10nodos, NGLT=798: ( BEAM1_T10.DAT)
Malla 2 – 129 nodos, 268 elementos Tetra4nodo, NGLT=387: ( BEAM2_T4.DAT)
Malla 2 – 639 nodos, 264 elementos Tetra10nodo, NGLT=1917: ( BEAM2_T10.DAT)
Malla 3 – 771 nodos, 2813 elementos Tetra4nodo, NGLT=2313: ( BEAM3_T4.DAT)
Malla 3 – 4844 nodos, 2813 elementos Tetra10nodo, NGLT=14532: ( BEAM3_T10.DAT)
Malla 4 – 1503 nodos, 5937 elementos, NGLT=4508: ( BEAM4_T4.DAT)
Malla 5 – 2103 nodos, 8834 elementos, NGLT=6309: ( BEAM5_T4.DAT)
Malla 6 – 3249 nodos, 14476 elementos, NGLT=9747: ( BEAM6_T4.DAT)
Malla 7 – 10041 nodos, 48465 elementos, NGLT=30123: ( BEAM7_T4.DAT)
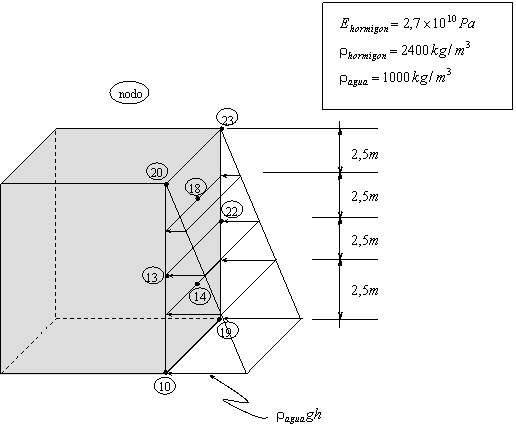
Ejemplo Presa Scalere (pg.255)
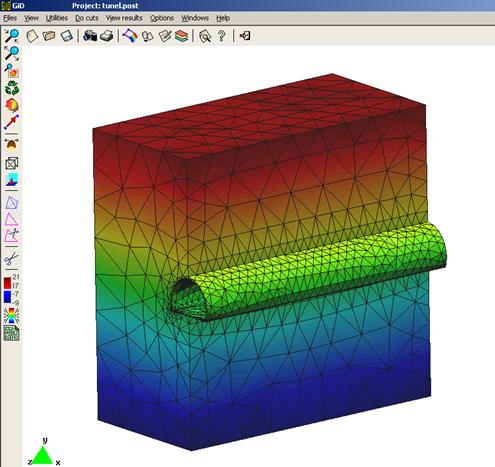
Ejemplo Túnel
Elasticidad Lineal – Matriz Constitutiva
Matriz Constitutiva Elástica (Tres dimensiones – 3D)
Fichero: MATD_3D.F
SUBROUTINE MATD_3D(YOUNG,POI,DMATX)
Input: YOUNG – Módulo de Young; POI – Coeficiente de Poisson.
Output: DMATX(6,6) – Matrix constitutiva elástica.
Tensor de Tensiones:
Tensor de deformaciones:
Relación tensión-deformación:
donde ![]() es la matriz constitutiva elástica. Para un material homogéneo, elástico, lineal e isótropo viene dada por:
es la matriz constitutiva elástica. Para un material homogéneo, elástico, lineal e isótropo viene dada por:
Las constantes de Lamé vienen dadas por
Matriz Constitutiva Elástica (Dos dimensiones – 2D))
Fichero: MATD_2D.F
SUBROUTINE MATD_2D(EST,E,POI,D)
Input: E – Módulo de Young; POI – Coeficiente de Poisson.
Output: D(4,4) – Matrix constitutiva elástica.
Si Tensión Plana (EST=1):
Si Deformación Plana (EST=2):
Estructuras
Elementos 1D
Celosías
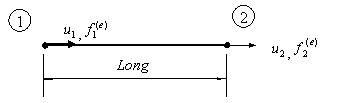
ELEMENTO BARRA
MATRIZ DE RIGIDEZ
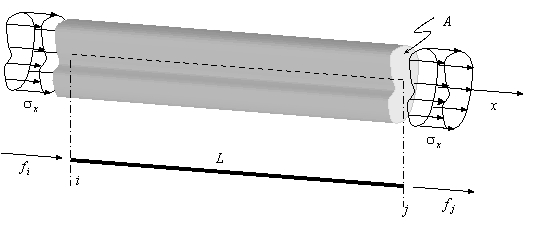
SUBROUTINE STIFBAR1D (E,A,LONG,KE)
Esta subrutina obtiene la matriz de rigidez de un elemento barra (1D) de sección constante.
Input: LONG-longitud de la barra. E-módulo de Young, A – Área de la sección transversal de la barra
Output: KE-matriz de rigidez –![]()
SUBROUTINE STIFBAR2D (L,M,E,A,LONG,KE)
Esta subrutina obtiene la matriz de rigidez (en el sistema de coordenadas globales X-Y) de un elemento barra cuya configuración está en el espacio bidimensional (2D). El elemento de barra presenta sección constante.
Input: L, M: cosenos directores, LONG-longitud de la barra. E-módulo de Young, A – Área de la sección de la barra
Output: KE-matriz de rigidez –![]()
SUBROUTINE STIFBAR3D (L,M,N,E,A,LONG,KE)
Esta subrutina obtiene la matriz de rigidez (en el sistema de coordenadas globales X-Y-Z) de un elemento barra cuya configuración está en el espacio tridimensional (3D). El elemento de barra presenta sección constante.
Input: L, M, N: cosenos directores, LONG-longitud de la barra. E-módulo de Young, A – Área de la sección transversal de la barra
Output: KE-matriz de rigidez –![]()
SUBROUTINE STIFBAR (NDIME,L,M,N,E,A,LONG,KE)
Esta subrutina obtiene la matriz de rigidez de un elemento barra de sección transversal constante.
Input: NDIME (dimensión); L, M, N: cosenos directores, LONG-longitud de la barra. E-módulo de Young, A – Área de la sección de la barra.
Output: KE(2*NDIME,2*NDIME)-matriz de rigidez –![]()
donde
NDIME=1 – caso 1D; NDIME=2 – caso 2D; NDIME=3 – caso 3D
CÁLCULO DE LA TENSIÓN EN EL ELEMENTO BARRA
SUBROUTINE TENSBAR (NDIME,L,M,N,E,LONG,UE,TENSX)
Esta subrutina obtiene la tensión en el elemento barra de sección transversal constante.
Input: NDIME: dimensión; L,M,N: cosenos directores; E: módulo de Young; LONG: longitud de la barra (sección constante), UE(2*NDIME): vector desplazamientos nodales del elemento (coordenadas globales)
Output: TENSX
CÁLCULO DE LOS ESFUERZOS EN EL ELEMENTO BARRA
SUBROUTINE ESFBAR (NDIME,KE,UE,FE)
Esta subrutina obtiene los esfuerzos en el elemento barra en las coordenadas globales.
Input: NDIME: dimensión; KE(2*NDIME,2*NDIME): matriz de rigidez del elemento barra (coordenadas globales); UE(2*NDIME): vector desplazamientos nodales del elemento (coordenadas globales).
Output: FE(2*NDIME)
POST-PROCESO – GID
SUBROUTINE GID_POST (NDIME, NGLN, NNE, NNODE, NELEM, NPROP, COR, ELE, PROPI, DESPL, FI_LOC)
Esta subrutina genera los ficheros para el post-proceso en GID
donde graban los resultados en los ficheros:
OPEN (10,FILE=ARQ(1:INDEX(ARQ,’.’,BACK=.TRUE.)-1)//’.POST.MSH’,STATUS=’UNKNOWN’)
OPEN (11,FILE=ARQ(1:INDEX(ARQ,’.’,BACK=.TRUE.)-1)//’.POST.RES’,STATUS=’UNKNOWN’)
ARQ=[nombre.dat]
[/vc_column_text][/vc_tta_section][vc_tta_section title=»Ejemplos de Celosías» tab_id=»1559807020093-16c786fd-952e»][vc_column_text]
SUBRUTINAS AUXILIARES
LISTEN.F – LECTURA DE DATOS
GID_POST.F – POST-PROCESO
CELOSÍAS 2D
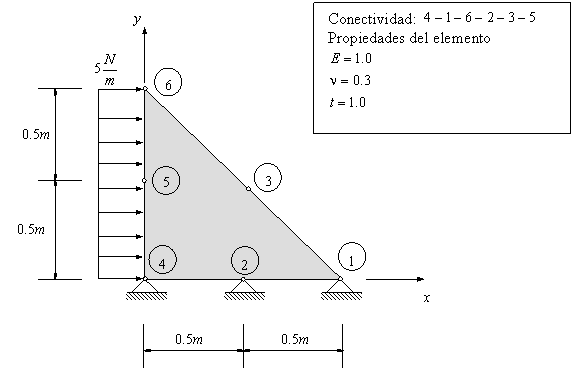
Ejemplo Computacional 4.2 (pg.181)
Coordenadas de los nodos:
| Nodos | ||
| 1 | 0 | 0 |
| 2 | 100 | 0 |
| 3 | 50 | 50 |
| 4 | 200 | 100 |
Características de las barras:
| Elemento | Área | Conectividad | ||
| Nodo i | Nodo j | |||
| 1 | 2 | 1 | 3 | |
| 2 | 2 | 3 | 2 | |
| 3 | 2 | 3 | 4 | |
| 4 | 2 | 2 | 4 | |
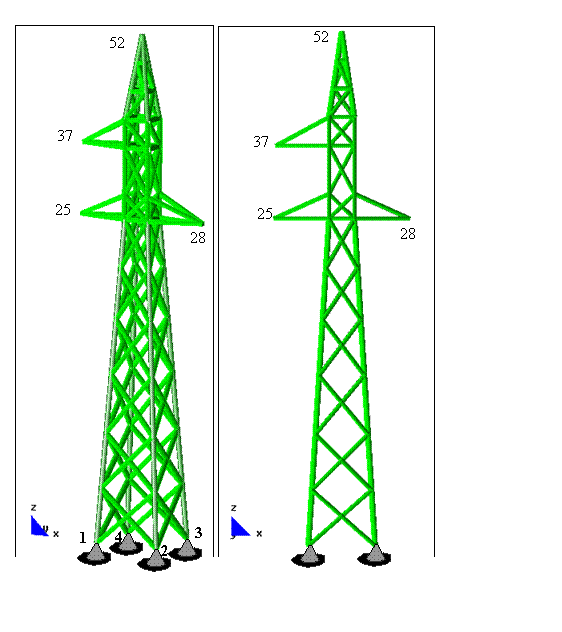
CELOSÍAS 3D
TORRE DE ALTA TENSIÓN
Fichero de datos: torre.dat
Referencia
Groenwold, A.A. & Stander, N. (1997). Optimal discrete sizing of truss structures subject to buckling constraints. Struct. Opt., 14:71-80.
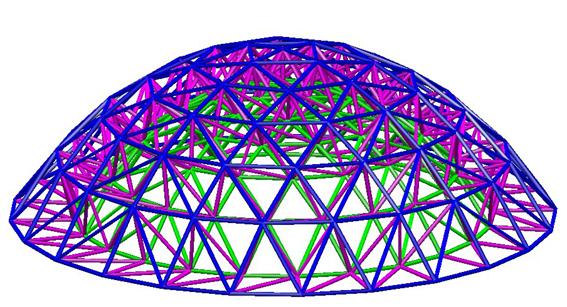
CÚPULA GEODÉSICA
Fichero completo: cupula.dat
[/vc_column_text][/vc_tta_section][vc_tta_section i_icon_fontawesome=»fa fa-asterisk» add_icon=»true» title=»Vigas» tab_id=»1559808049550-4794863f-ba32″][vc_column_text]
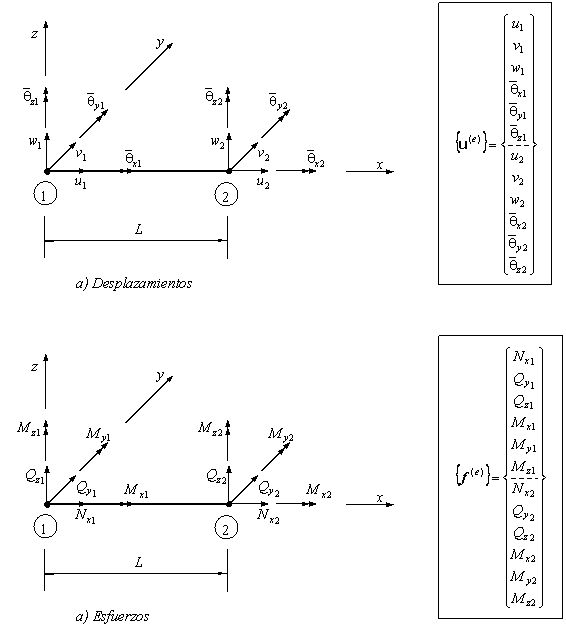
ELEMENTO VIGA
Matriz de rigidez en el sistema local
MATRIZ DE RIGIDEZ
SUBROUTINE VIGGLO (L,C,S,YOUNG,NU,JT,IY,KE)
Esta subrutina obtiene la matriz de rigidez (en coordenadas globales) de un elemento de viga con tres grados de libertad por nudo.
Input: L-longitud de la viga. C,S cosenos directores. YOUNG-módulo de Young, NU-coeficiente de poisson. IY-Momento de inercia a flexión. JT-momento de inercia efectivo a torsión
Output: KE-matriz de rigidez (coordenadas globales XYZ) – ![]()
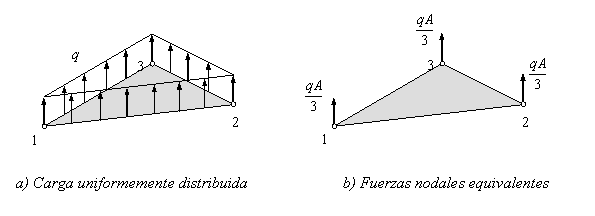
VECTOR DE FUERZAS NODALES EQUIVALENTES
SUBROUTINE NOEQ (L,C,S,Q,MT,FE_EQ)
Esta subrutina obtiene el vector de fuerzas nodales equivalentes (coordenadas globales) de un elemento de viga.
Input: L-longitud de la viga. C,S – cosenos directores. Q-carga uniformemente distribuida. MT- momento torsor distribuido en la viga
Output: FE_EQ(6)-vector con fuerzas nodales equivalente – ![]()
VECTOR DE ESFUERZOS
SUBROUTINE ESFVIG(L,C,S,YOUNG,NU,JT,IY,Q,MT,DE,FE_ESF)
Esta subrutina calcula los esfuerzos (coordenadas locales) en el elemento de viga
Input: L-longitud del elemento. C,S-cosenos directores, YOUNG-módulo de Young. NU-coeficiente de poisson. Q-carga uniformemente distribuida. MT-momento de torsión uniformemente distribuido. DE(6)- vector de los desplazamientos (coordenadas globales)
Output: FE_ESF(6) – esfuerzos en el elemento de viga (coordenadas locales).
[/vc_column_text][/vc_tta_section][vc_tta_section title=»Ejercicios de Vigas» tab_id=»1559808406858-8978c830-fd38″][vc_column_text]
Subrutinas de apoyo
Ejercicio académico 1
Datos:
Solución analítica
Desplazamiento máximo (centro): ![]()
Solución numérica
Fichero de entrada: viga1.dat
Fichero de resultado: viga1.sol
Ejercicio académico 2
Datos:
Solución analítica
Desplazamiento máximo (centro):![]()
Solución numérica
Fichero de entrada: viga2.dat
Fichero de resultado: viga2.sol
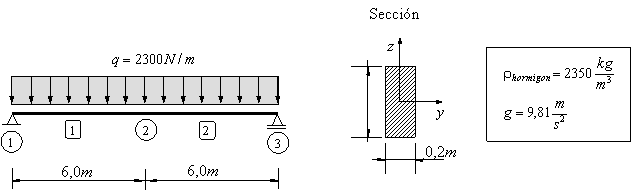
Ejercicio académico 3
Datos:
Momento a flexión de las vigas: ![]() ,
,![]() ,
, ![]()
Solución numérica
Fichero de entrada: viga3.dat
Fichero de resultado: viga3.sol
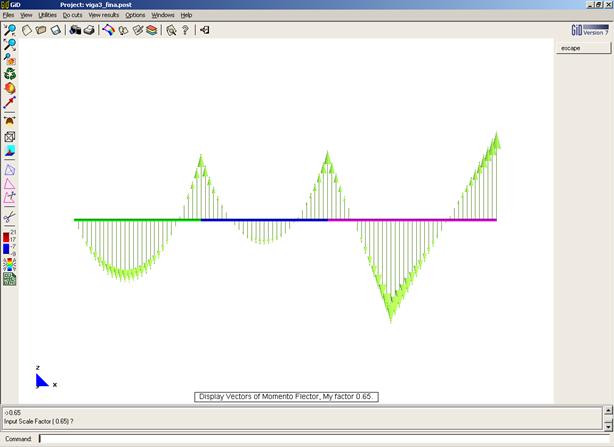
Post-proceso GID (100 elementos)
Momento Flector en las vigas
Convenio de signos – Positivo si tracciona fibras superiores
Ejercicio académico 4
Datos:
Momento de inercia efectivo a torsión:![]()
Momento a flexión de las vigas:![]()
Carga uniformemente distribuida en las vigas:![]()
Fichero de datos: viga4.dat
Fichero de solución: viga4.sol
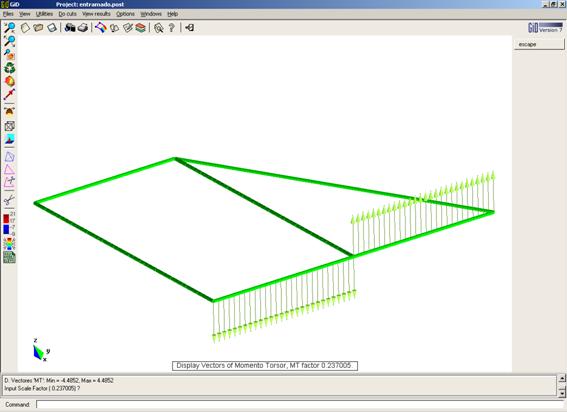
Post-proceso GID (229 elementos) [entramado.dat]
Momento Flector en las vigas
Convenio de signos – Positivo si tracciona fibras superiores
Momento Torsor en las vigas
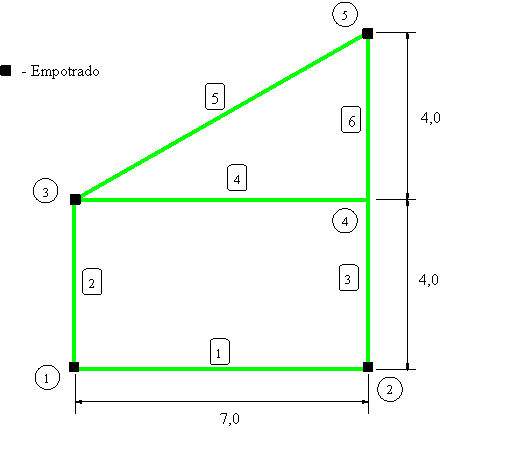
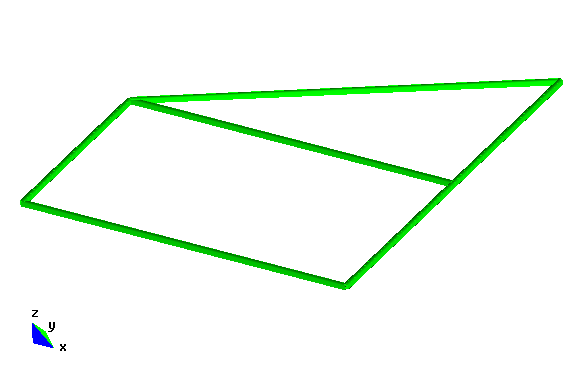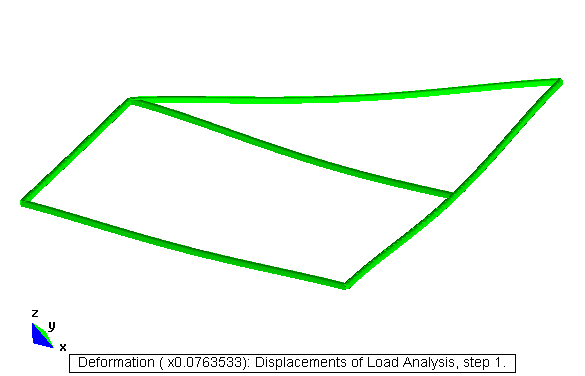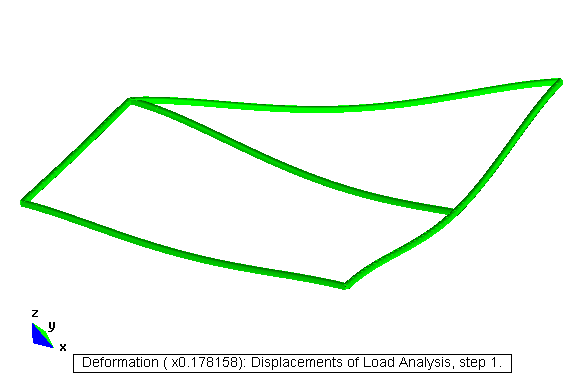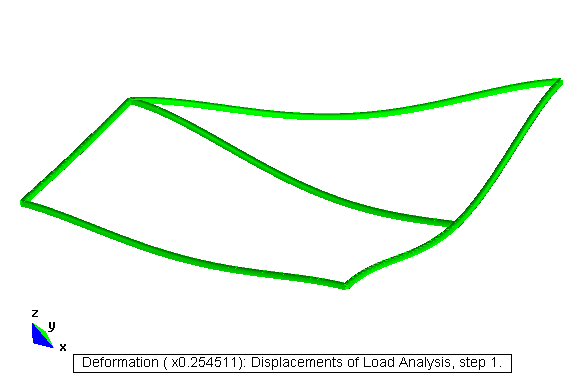
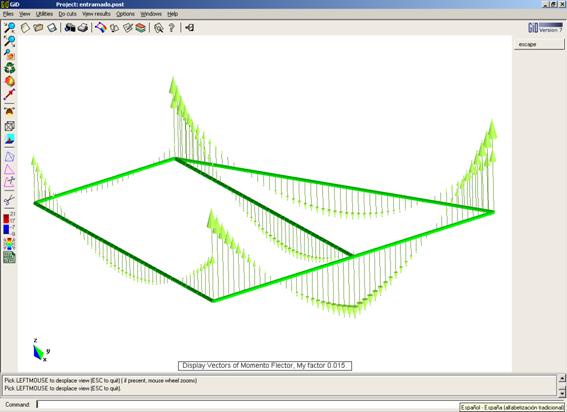
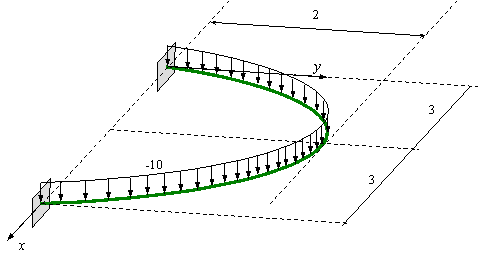
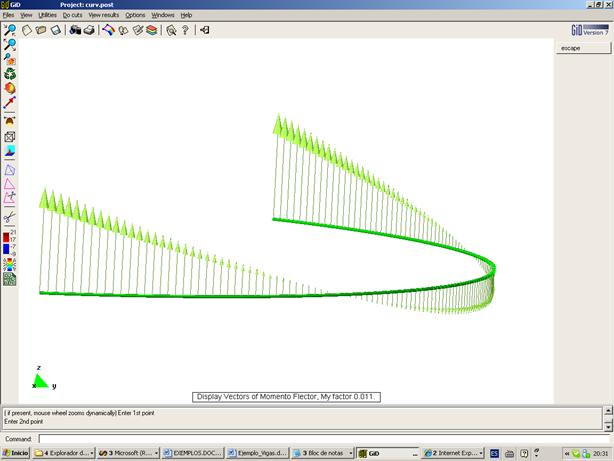
Ejercicio académico 5
Fichero de datos: [curv.dat]
Deformación
Momento Flector en las vigas
Convenio de signos – Positivo si tracciona fibras superiores
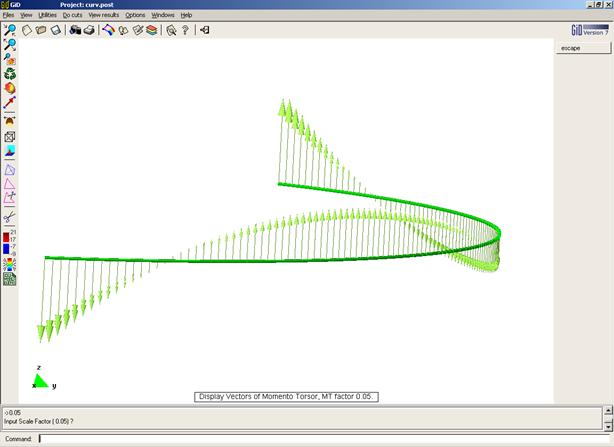
Momento Torsor
 [/vc_column_text][/vc_tta_section][vc_tta_section title=»Vigas – Base Elástica» tab_id=»1559812685977-33ff47db-f356″][vc_column_text]
[/vc_column_text][/vc_tta_section][vc_tta_section title=»Vigas – Base Elástica» tab_id=»1559812685977-33ff47db-f356″][vc_column_text]
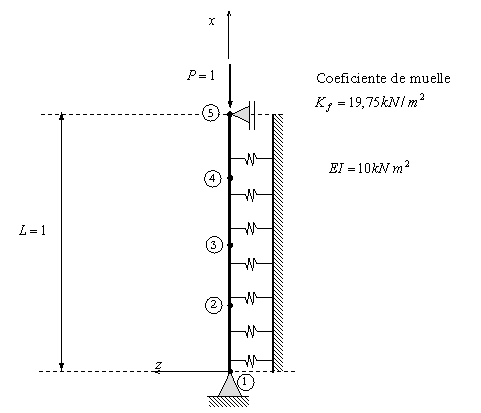
Viga base elástica demostración
ELEMENTO VIGA
Matriz de rigidez en el sistema local
donde
MATRIZ DE RIGIDEZ
SUBROUTINE STIFVIG01 (L,YOUNG,IY,KE)
Esta subrutina obtiene la matriz de rigidez de un elemento de viga con dos grados de libertad por nudo.
Input: L-longitud de la viga. YOUNG-módulo de Young, IY-Momento de inercia a flexión.
Output: KE-matriz de rigidez –![]()
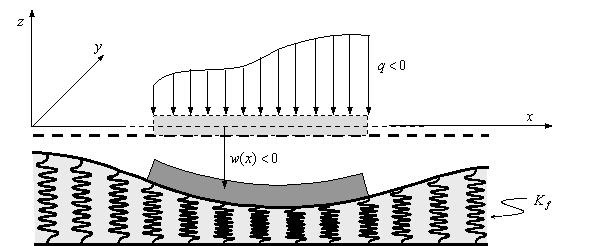
SUBROUTINE STIFVIG02 (L,KF,KE)
Esta subrutina obtiene la matriz de rigidez de un elemento de viga sobre la base elástica.
Input: L-longitud de la viga. KF-coeficiente de muelle.
Output: KE-matriz de rigidez –![]()
VECTOR DE FUERZAS NODALES EQUIVALENTES
SUBROUTINE NOEQ01 (L,Q,FE_EQ)
Esta subrutina obtiene el vector de fuerzas nodales equivalentes de un elemento de viga.
Input: L-longitud de la viga. Q-carga uniformemente distribuida.
Output: FE_EQ(4)-vector con fuerzas nodales equivalente –![]()
VECTOR DE ESFUERZOS
SUBROUTINE ESFVIG01(L,YOUNG,IY,Q,KE,DE,FE_ESF)
Esta subrutina calcula los esfuerzos en el elemento de viga
Input: L-longitud del elemento. YOUNG-módulo de Young. Q-carga uniformemente distribuida. KE(4)-matriz de rigidez de la viga. DE(4)- vector desplazamientos del elemento
Output: FE_ESF(4) – esfuerzos en el elemento de viga.
Carga Crítica
Ejercicio académico 1
Solución (6 elementos finitos)
Fichero de entrada: viga1.dat
Fichero de resultado: viga1.sol
Ejercicio académico 2
Solución (4 elementos finitos)
Fichero de entrada: viga2.dat
Fichero de resultado: viga2.sol
Ejercicio académico 3
Solución (4 elementos finitos)
Fichero de entrada: viga3.dat
Fichero de resultado: viga3.sol
[/vc_column_text][/vc_tta_section][vc_tta_section i_icon_fontawesome=»fa fa-asterisk» add_icon=»true» title=»Pórtico Espacial» tab_id=»1559814335505-8db30d55-6381″][vc_column_text]
ELEMENTO PÓRTICO ESPACIAL
Matriz de Rigidez en el Sistema Local
Características del material y geométricas
Como estamos en el régimen elástico lineal, para obtener la matriz de rigidez vamos utilizar el principio de la superposición.
Haciendo la contribución de cada grado de libertad correspondiente, obtenemos:
Subroutine STIFPOR3D.F
Matriz de Rigidez en el Sistema Global
Conocidos los vectores ![]() y
y ![]() en el sistema global. La ley de transformación del sistema global al sistema local viene representada por la matriz donde se cumple que:
en el sistema global. La ley de transformación del sistema global al sistema local viene representada por la matriz donde se cumple que: ![]() y
y ![]() . Con eso concluimos que:
. Con eso concluimos que:
A continuación definiremos la matriz de transformación ![]() .
.
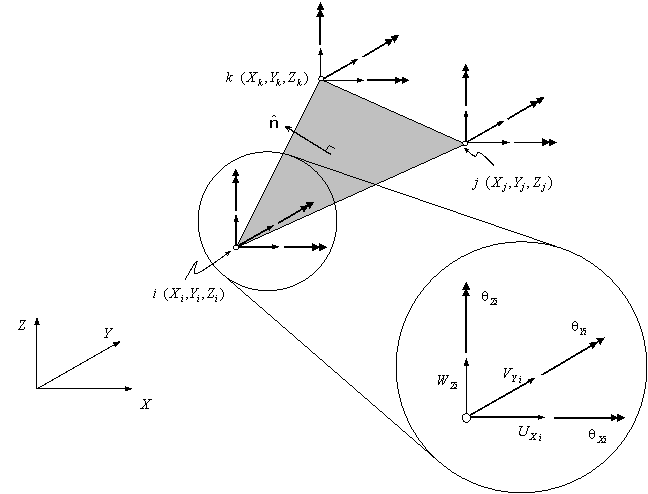
Necesitamos definir tres nodos ![]()
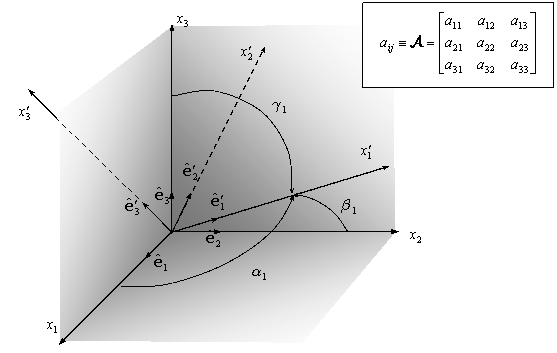
Sistema Local
- : según dirección .
El versor según dirección viene dado por:
donde
- Versor según dirección .
donde
- : normal al elemento de superficie,
- : Según la convención
.
Matriz de transformación del sistema al sistema local está constituida por los versores , i.e.:
Luego, la matriz de transformación viene dada por:
Bibliografía
GERE, J.M. & W. WEAVER JR. (1965). Analysis of Framed Structures. Van Nostrand Reinhold, U.S.
Placas
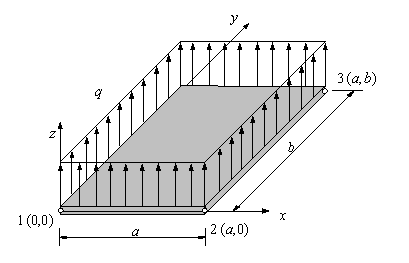
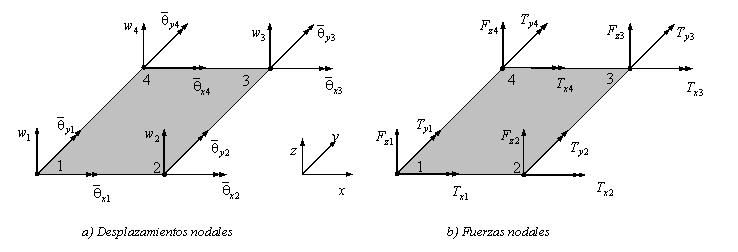
ELEMENTO ACM
MATRIZ DE RIGIDEZ – ACM
SUBROUTINE STIFACM (A,B,NU,D,Q,KE)
Calcula matriz de rigidez (explícitamente) del elemento de placa a flexión (elemento ACM).
donde A,B: dimensiones de la placa, NU: poisson, ![]() con E: módulo de Young; t: espesor; Q- carga uniformemente distribuida
con E: módulo de Young; t: espesor; Q- carga uniformemente distribuida
Figura: Grados de libertad y fuerzas nodales – elemento ACM.
VECTOR DE FUERZAS NODALES EQUIVALENTE – ACM
SUBROUTINE FNOACM (A,B,Q,FE)
Calcula matriz de rigidez (explícitamente) del elemento de placa a flexión (elemento ACM).
ELEMENTO DKT
Referencia
Jeyachandrabose,C.; Kirkhope,J. & Ramesh Babu, C. (1985). An alternative explicit formulation for DKT plate-bending element. Int.J. Num. Meth. Eng., 21:1289-1293.
MATRIZ DE RIGIDEZ – DKT
SUBROUTINE STIFDKT (T,E,NU,X,Y,KE)
Calcula matriz de rigidez (explícitamente) del elemento de placa a flexión (elemento ACM).
donde A,B: dimensiones de la placa, NU: poisson, ![]() con E: módulo de Young; t: espesor; Q- carga uniformemente distribuida
con E: módulo de Young; t: espesor; Q- carga uniformemente distribuida
SUBRUTINA AUXILIAR
SUBROUTINE MATD (T,YOUNG,NU,D)
Input: T: espesor; YOUNG: módulo de young; NU: poisson
Output: D(3,3) – matriz que contiene la rigidez a flexión y a torsión de la placa
VECTOR DE FUERZAS NODALES EQUIVALENTES – DKT
SUBROUTINE FNODKT (AREA,Q,FE)
Input: AREA: área del elemento triangular; Q: carga uniformemente distribuida
Output: FE(9)
ESFUERZOS EN EL ELEMENTO – DKT
SUBROUTINE MOMDKT (T,YOUNG,NU,X,Y,UE,MXT,MYT,MXYT)
Input: T: espesor, YOUNG: módulo de young; NU: poisson; X(3),Y(3): coordenadas de los nodos; UE(12): desplazamientos nodales y centroide
Output: MX(5);MY(5); MXY(5): momentos
ELEMENTO DKT4 (pag. 291)
Este elemento está formado a partir de 4 elementos DKT a través de una condensación estática.
[/vc_column_text][/vc_tta_section][vc_tta_section title=»Ejercicios de Placas» tab_id=»1559893398181-685a2f0e-d146″][vc_column_text]
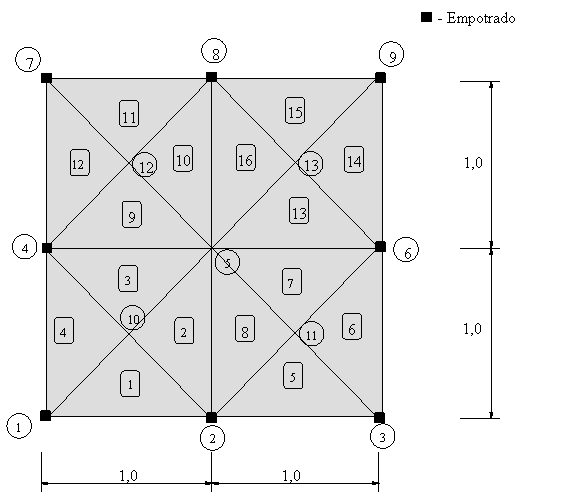
Ejercicio académico 1
Elemento utilizado – DKT
Datos:
Carga uniformemente distribuida en las losas: ![]()
Fichero de datos: placa1.dat
Fichero de solución: placa1.sol
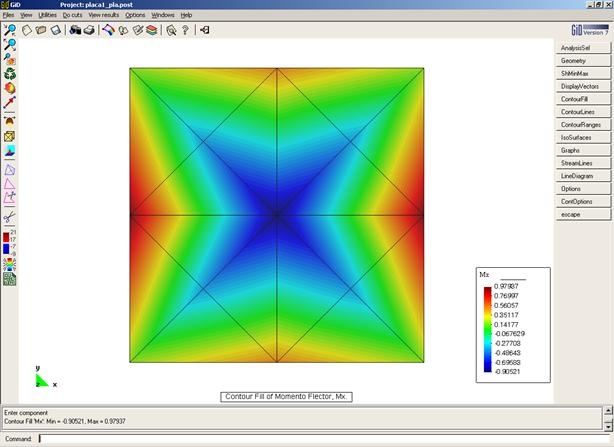
Post-proceso GID (Momento flector – Mx
Ejercicio académico 2
Elemento utilizado – DKT4 (Condensación estática)
Datos:
Carga uniformemente distribuida en las losas:![]()
Fichero de datos: placa2.dat
Fichero de solución: placa2.sol
OBS.: Los resultados de los dos problemas planteados tiene que tener los mismos resultados.
Ejercicio académico 3
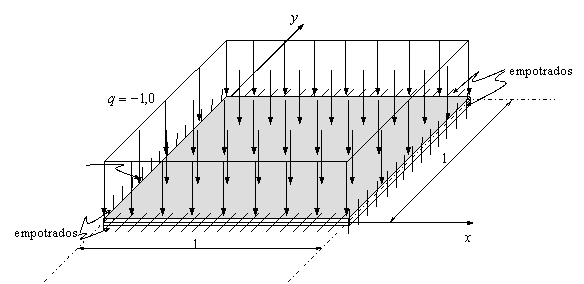
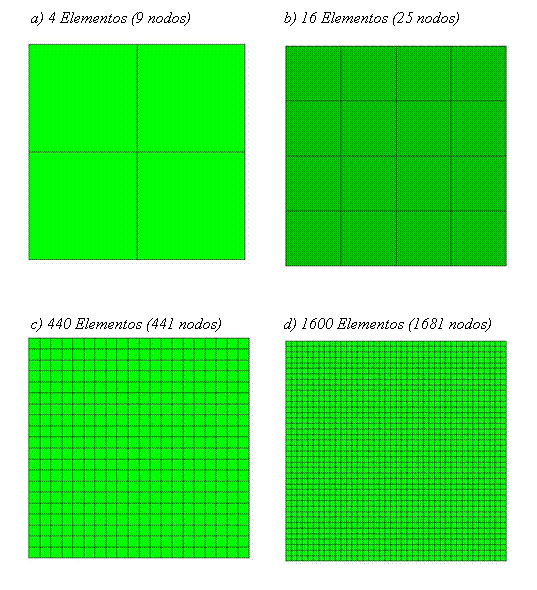
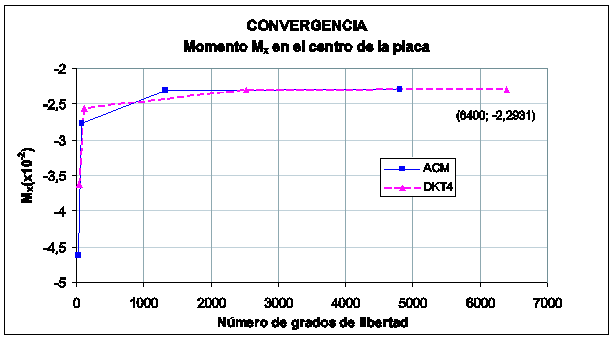
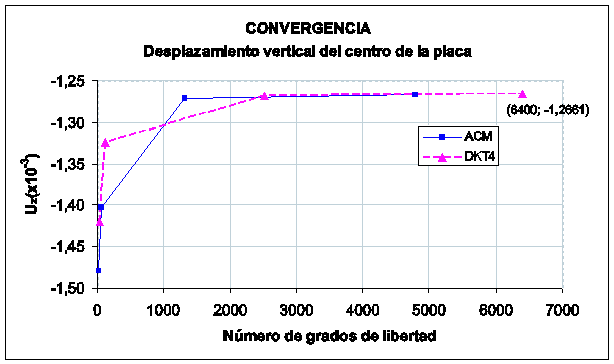
En este ejemplo se compara la convergencia de 2 elementos: ACM y DKT4.
Carga uniformemente distribuida en las losas: ![]()
Ejercicio académico 1
Fichero de datos: [plavig.dat]
Solución: [plavig.sol]
Ejercicio académico 2
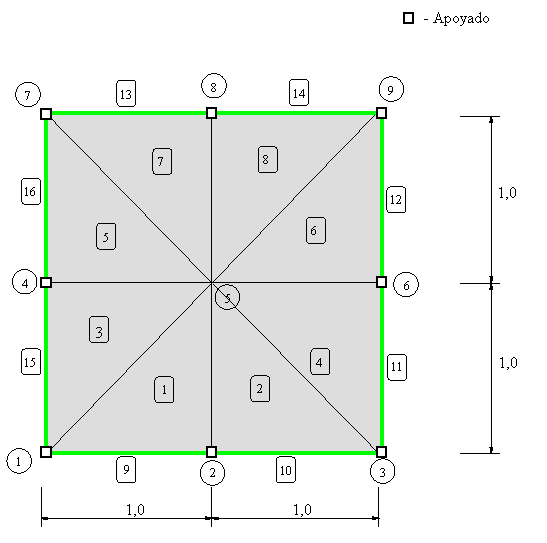
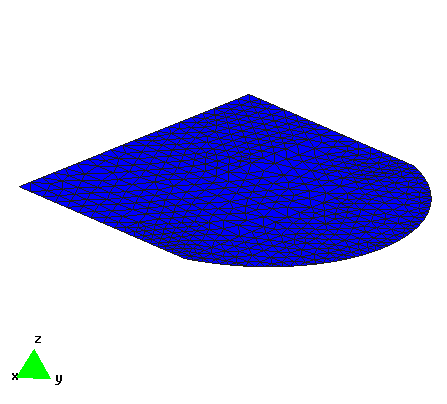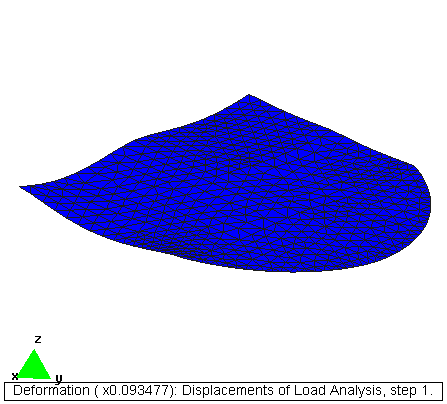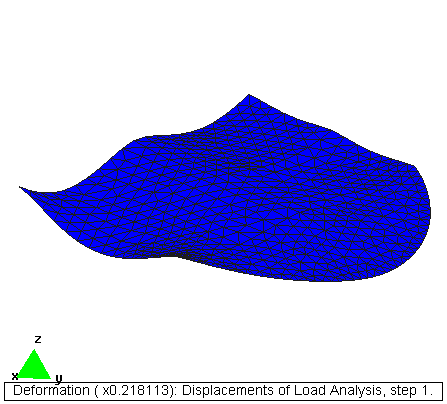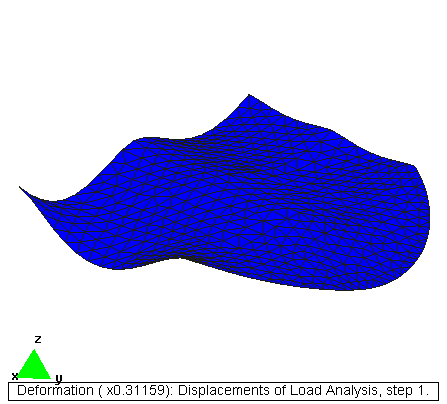
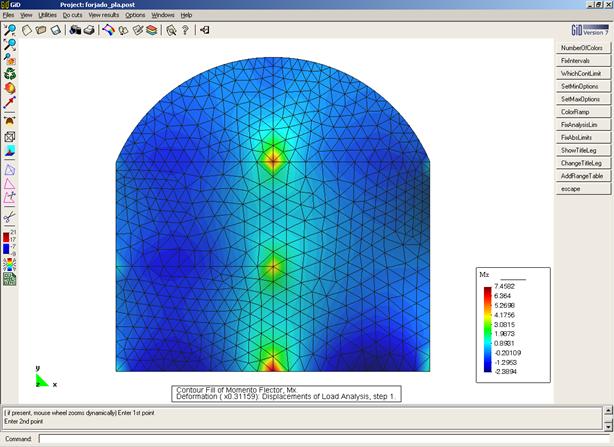
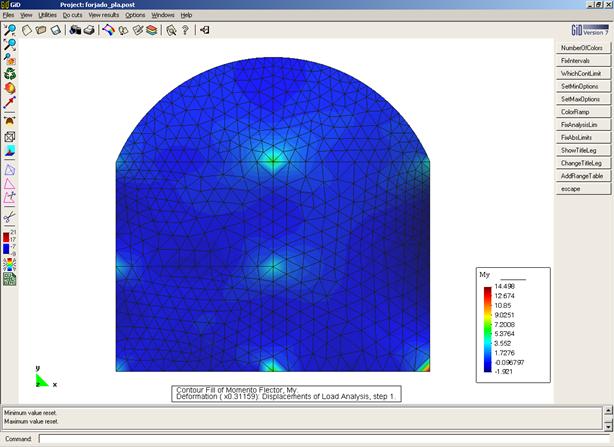
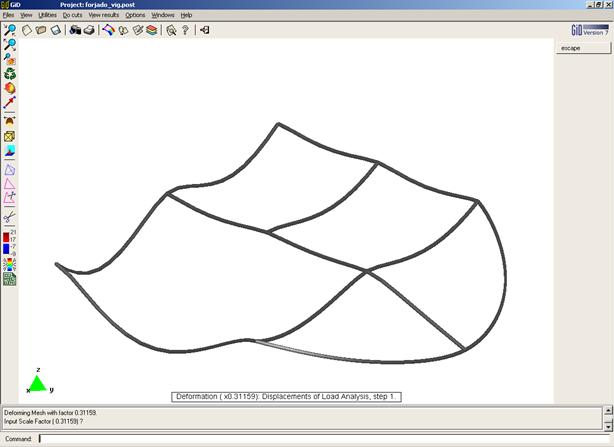
Fichero de datos: [forjado.dat]
Deformación
Momento Flector Mx
Momento Flector My
DEFORMACIÓN DE LAS VIGAS
Cáscaras
ELEMENTO CST+DKT
Grados de libertad del elemento (Sistema ![]() )
)
donde ![]() es la matriz de rigidez del elemento CST+DKT.
es la matriz de rigidez del elemento CST+DKT.
MATRIZ DE RIGIDEZ – CST+DKT
Sistemas de Referencia Local
El versor según dirección viene dado por:
donde
Definición del versor según dirección ![]()
Denominamos así los cosenos directores del eje ![]() por:
por:
Denominamos así los cosenos directores del eje ![]() por:
por:
Coordenadas de los nodos en el sistema local:
Nodo 1:
Nodo 2:
Nodo3:
donde
Matriz de transformación del sistema ![]() al sistema local
al sistema local ![]() está constituida por los versores
está constituida por los versores ![]() , i.e.:
, i.e.:
Grados de Libertad en el Sistema Local
En esta situación podemos construir las matrices de rigideces de los elementos CST (![]() ) y DKT (
) y DKT (![]() ).
).
Matriz de Rigidez del CST (sistema local)
Matriz de Rigidez del DKT (sistema local)
Vector desplazamiento nodales del elemento CST+DKT (Sistema local)
Teniendo en cuenta el orden de los grados de libertad anteriores, podemos hacer la contribución en la matriz del elemento CST+DKT en el sistema local, resultando en la matriz ![]() :
:
El último paso es transformar esta matriz para el sistema global a través de la matriz de transformación:
donde
Ejercicios de Cáscaras
EJEMPLO – VIGA-CAJÓN EMPOTRADA
Fichero de Datos: CAJONDKT.DAT
Post-proceso: Desplazamientos (Dirección Y):
(Dirección Z)
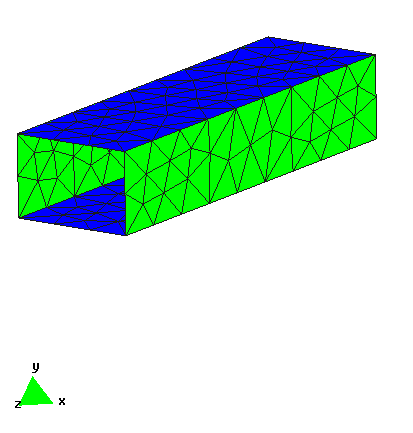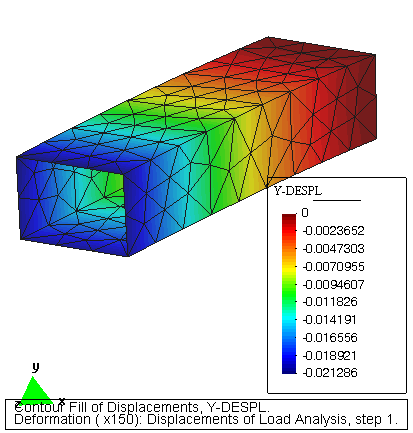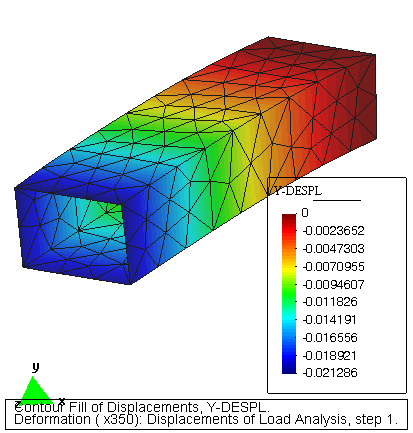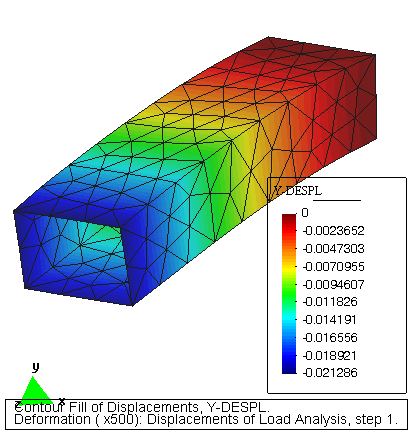
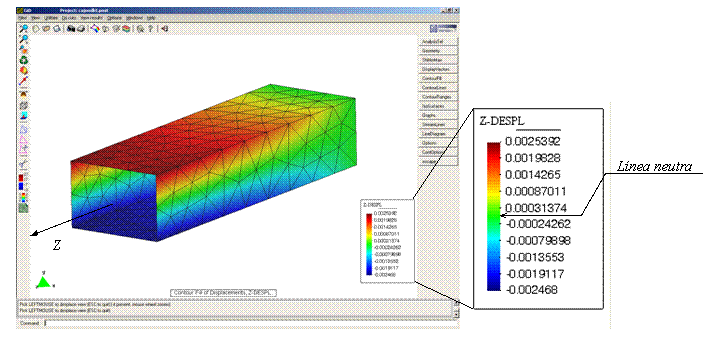
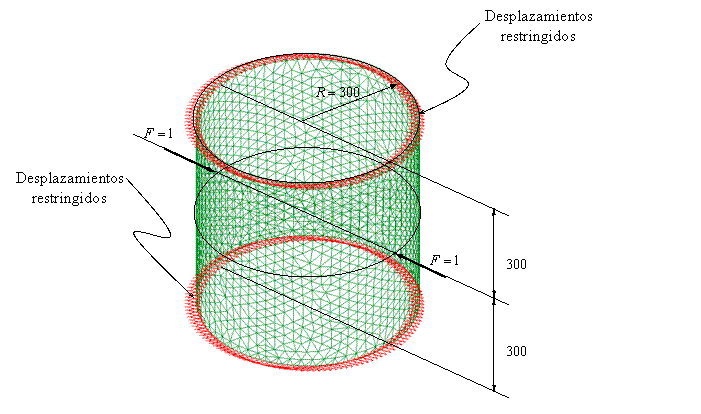
EJEMPLO – CILINDRO
Fichero de Datos: CYLINDER3.DAT
Post-proceso: Desplazamientos
Ver apuntes página 350
Ejemplo académico 1
Fichero de entrada: [torsion1.dat]
Fichero de resultados: [torsion1.sol]
Mismo ejemplo con malla más refinada
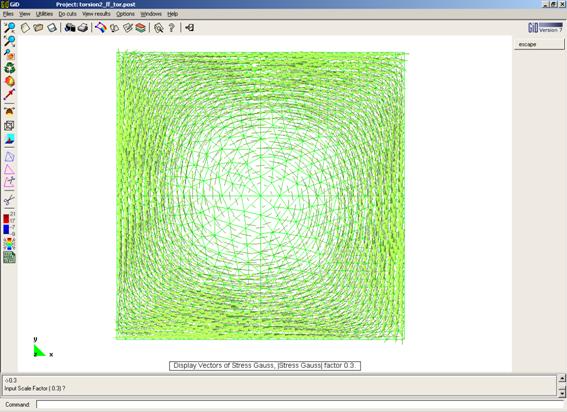
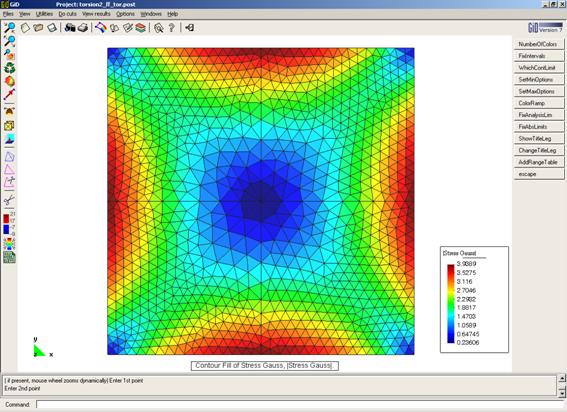
Fichero de entrada: [torsion2_ff.dat]
Fichero de resultados: [torsion2_ff.sol]
Deformación del membrana
Distribución de tensiones tangenciales (centroide de los elementos)
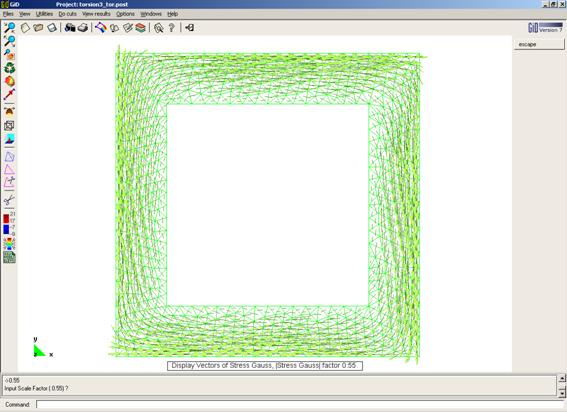
Ejemplo académico 2
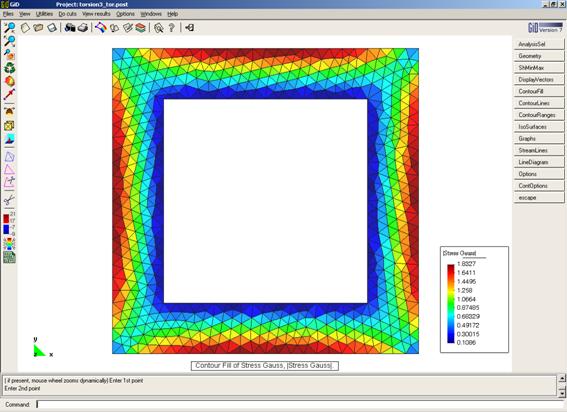
Fichero de entrada: [torsion3.dat]
Fichero de resultados: [torsion3.sol]
Deformación de la membrana
Flujo de tensiones
Distribución de tensiones tangenciales (centroide de los elementos)
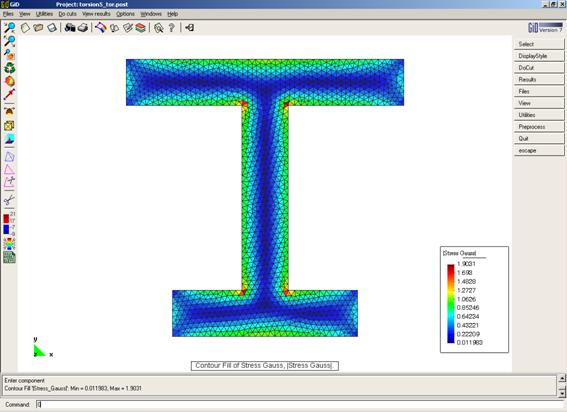
Ejemplo académico 3
Fichero de entrada: [torsion5.dat]
Fichero de resultados: [torsion5.sol]
Deformación de la membrana
Distribución de tensiones tangenciales (centroide de los elementos)
Ecuación convección-difusión – Pág. 313
donde
![]() – flujo de calor (Ley de Fourier)
– flujo de calor (Ley de Fourier)
![]() -tensor de conductividad térmica
-tensor de conductividad térmica
Sistema de Ecuaciones discretas (MEF)
donde
(incógnitas, temperaturas nodales)
Las expresiones de ![]() ,
, ![]() ,
, ![]() vienen dadas por:
vienen dadas por:
![]() donde
donde ![]() -coeficiente de transferencia de calor convectivo
-coeficiente de transferencia de calor convectivo
Las expresiones de ![]() ,
,![]() ,
,![]() vienen dadas por:
vienen dadas por:
Caso Transitorio – Resolución del Sistema
Consideremos el siguiente sistema de ecuaciones:
| (1) |
Para el problema térmico ![]() es la matriz de capacitancia,
es la matriz de capacitancia, ![]() es la matriz de conductividad, y
es la matriz de conductividad, y ![]() es el vector con los valores nodales de la temperatura.
es el vector con los valores nodales de la temperatura.
Considerando que:
| (2) |
Además aplicando el método alfa:
| (3) |
donde ![]() . Para
. Para ![]() (método explícito) y es ventajosa si la matriz
(método explícito) y es ventajosa si la matriz ![]() es diagonal. Para
es diagonal. Para ![]() (método implícito).
(método implícito).
Reemplazando (2) y (3) en la expresión (1), obtenemos que:
| (4) |
| (5) |
Resultando que:
| (6) |
Subroutinas
Caso 2D – Elemento triangular de 3 nodos
Matriz de Conductividad Térmica
SUBROUTINE STIFT3(AREA,B,C,KX,KY,KE)
Obtiene la matriz de conductividad térmica [KE] – Elemento triangular de 3 nodos.
Input: AREA,
B(1)=Y2-Y3,B(2)=Y3-Y1,B(3)=Y1-Y2,C(1)=X3-X2,C(2)=X1-X3,C(3)=X2-X1
KX,KY: Coeficientes de conductividad térmica.
Output: KE(3,3) – Matriz de conductividad térmica – Elemento triangular de 3 nodos – Prob. Térmico 2D.
Matriz de Convectividad Térmicaç
SUBROUTINE STIFTC3(XC,ALPHA,N1,N2,KE_2)
Obtiene la matriz de convectividad térmica – Elemento triangular de 3 nodos.
Input: XC(Coordenadas nodales), ALPHA-Coeficiente de convectividad -N1,N2 (nodos locales asociados al lado convectivo)
Output: KE_2(3,3) – Matriz de convectividad – Elemento triangular de 3 nodos – Prob. Térmico 2D.
Matriz de Capacitancia Térmica
SUBROUTINE STIFTM3(AREA,DENSI,CV,KEM)
Obtiene la matriz de capacitancia [KEM] para problema de temperatura – Elemento triangular de 3 nodos.
Input: AREA, DENSI-densidad; CV-calor específico.
Output: KEM(3,3) – Matriz de capacitancia del elemento triangular de 3 nodos – Prob. Térmico 2D.
Término Independiente
SUBROUTINE P2DT3_1(XC,FUENTE,DENSI,PE_1)
Obtiene el vector de fuerza debido a la fuente interna – [PE_1] – Elemento triangular de 3 nodos.
Input: XC(Coordenadas nodales), FUENTE-Fuente interna, DENSI: densidad.
Output: PE_1(3)
Términos Independientes
SUBROUTINE P2DT3_23(XC,VALOR,LADO,PE_23)
Obtiene el vector de fuerzas – Flujo prescrito [FE_2] o Convectivo [FE_3] – 2D.
[FE_2]=> VALOR=q_pre (flujo prescrito- )
[FE_3]=> VALOR=ALPHA*T_EXT ()
Ejercicios de Flujo Térmico I (Estacionario)
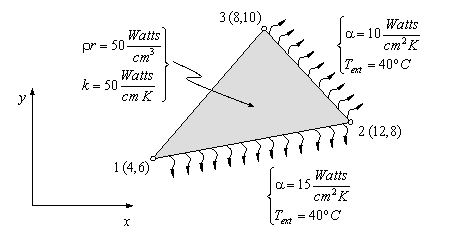
Ejercicio académico 1
Problema de flujo térmico estacionario en 2D.
![]() -densidad,
-densidad, ![]() -fuente interna de calor,
-fuente interna de calor, ![]() -coeficiente de conductividad térmico
-coeficiente de conductividad térmico
![]() -coeficiente de transferencia de calor convectivo,
-coeficiente de transferencia de calor convectivo, ![]() -temperatura externa.
-temperatura externa.
Ficheros
Fichero de entrada: temp1.dat
Fichero de resultado: temp1.sol
Valores detallados de las matrices para la comprobación del programa:
Matriz de rigidez:
con
Parte debido a la conducción:
Parte debido a la convección
Parte transitoria debido a la difusividad
Término Independiente
Parte
Parte
Parte
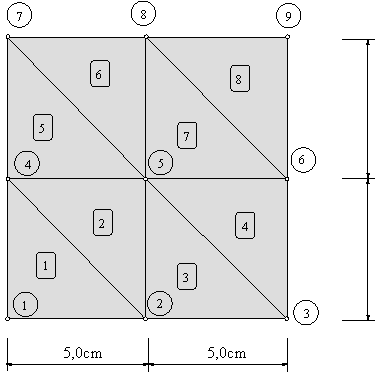
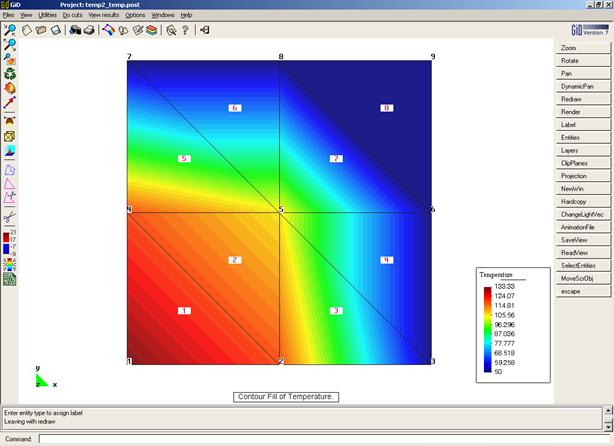
Ejercicio académico 2
Problema de flujo térmico estacionario en 2D.
Discretización
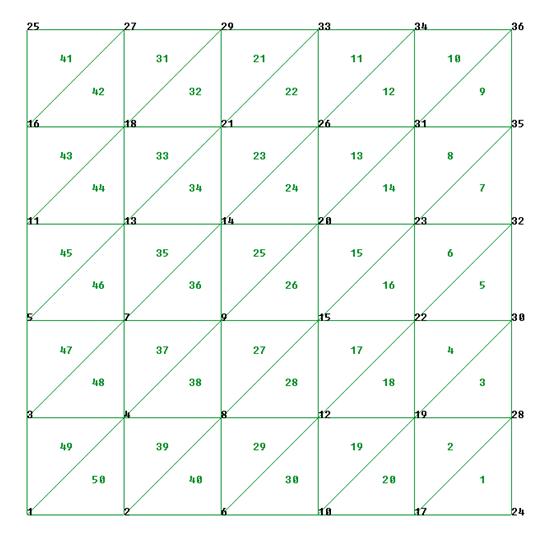
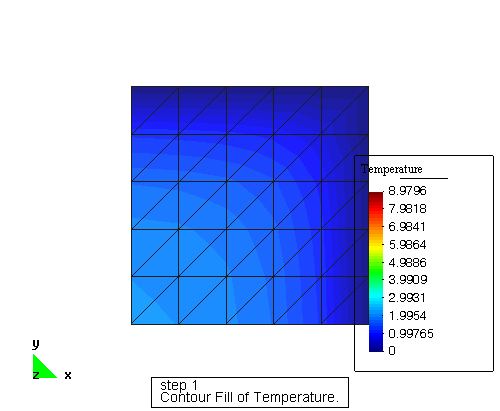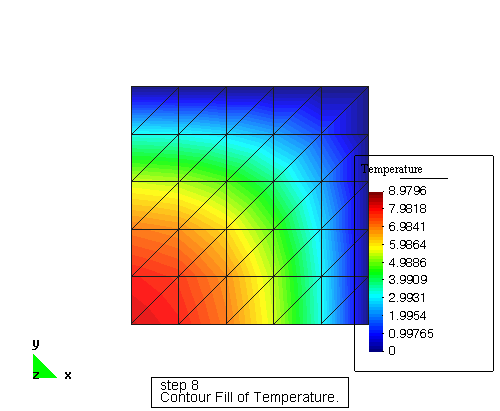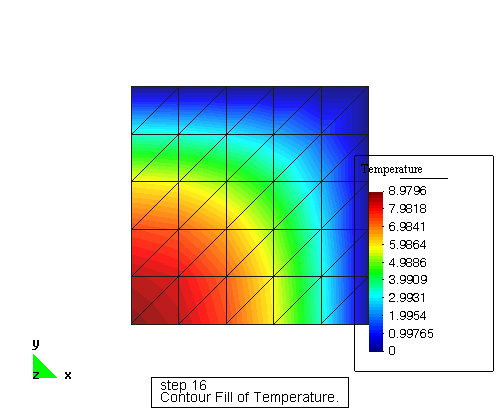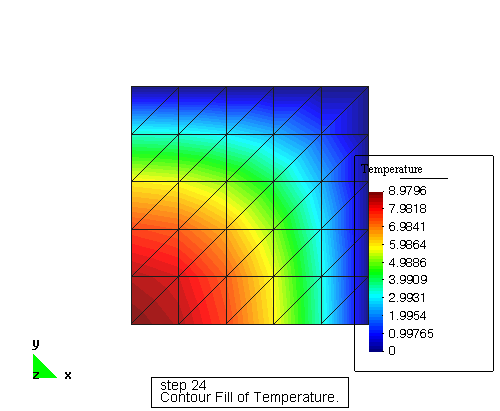
Ficheros
Fichero de entrada: temp2.dat
Fichero de resultado: temp2.sol
Post-Proceso – GID
Ejercicio académico 3
Problema de flujo térmico estacionario en 3D – Tetraedro de 4 Nodos
Ficheros
Fichero de entrada: temp3d1.dat
Fichero de resultado: temp3d1.sol
Valores detallados de las matrices para la comprobación del programa:
Matriz de rigidez:
con
Parte debido a la conducción:
Parte debido a la convección
Parte transitoria debido a la difusividad
Término Independiente
Parte
Parte
Parte
Ejercicio académico 4
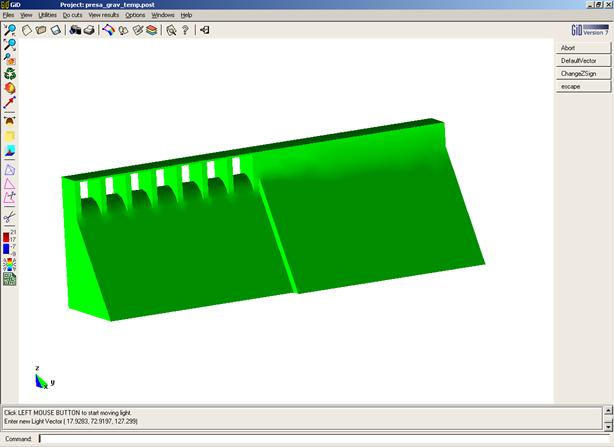
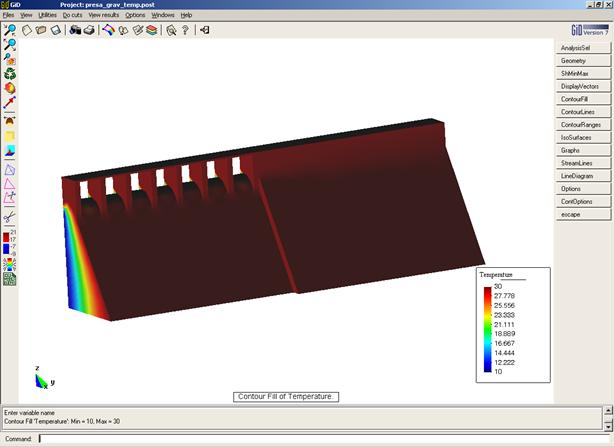
Presa
Ejercicio académico 1
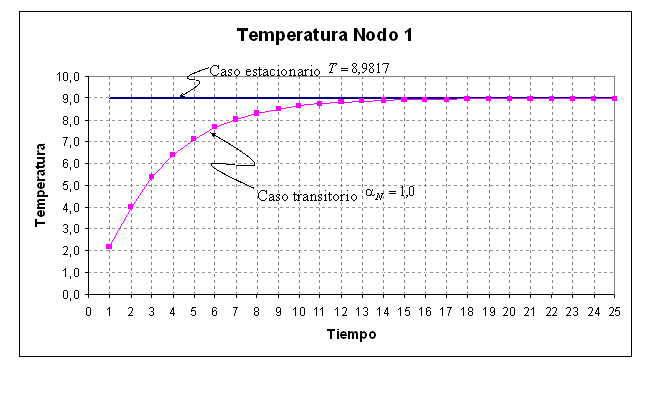
Problema de flujo térmico transitorio en 2D.
Ficheros
Fichero de entrada: ejemplo4_2.dat
Fichero de resultado: ejemplo4_2.sol
Discretización
POST-PROCESO – GID
Ejercicio académico 1
Problema de filtración en medio poroso (flujo confinado), estacionario en 2D.
DATOS
![]() -coeficiente de permeabilidad;
-coeficiente de permeabilidad;
Ficheros
Fichero de entrada: flujo1.dat
Fichero de resultado: flujo1.sol
Discretización
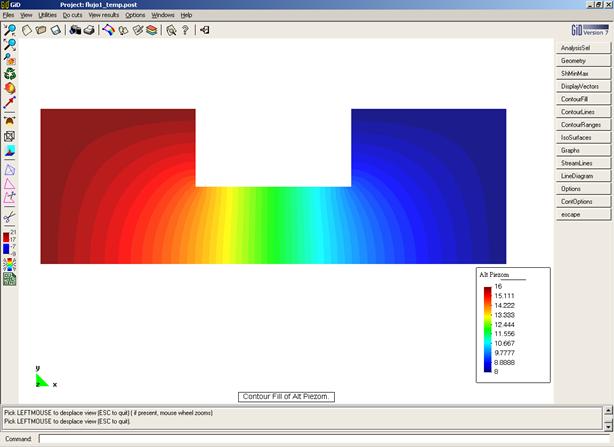
Altura piezométrica
Nodos
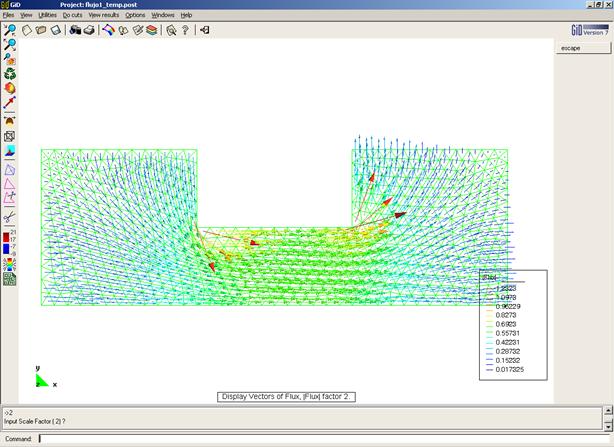
Flujo
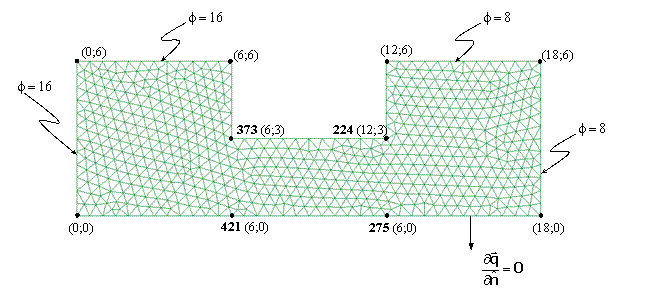
Ejercicio académico 2
Problema de filtración en medio poroso (flujo confinado), transitorio.
Ficheros
Fichero de entrada: flujo2.dat
Fichero de resultado: flujo2.sol