|
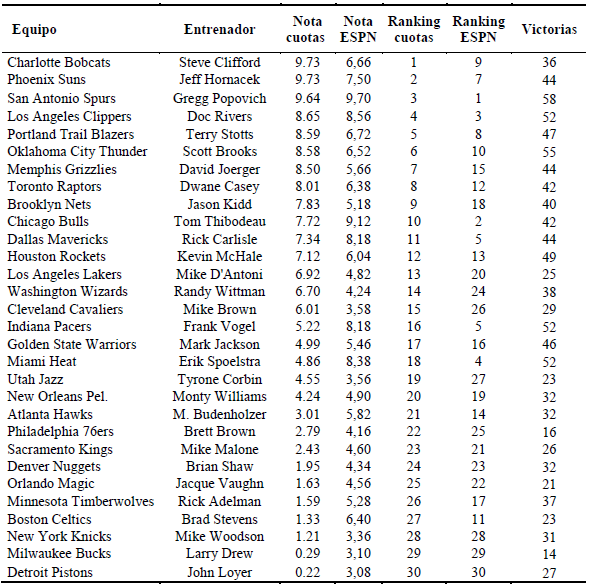
Equipo
|
Entrenador
|
Eficiencia
|
Victorias
|
|
Valencia Basket
|
Velimir Perasovic
|
0.9997
|
30
|
|
Real Madrid
|
Pablo Laso
|
0.9585
|
31
|
|
Cajasol
|
Aito G. Reneses
|
0.9364
|
18
|
|
Herbalife Gran Canaria
|
Pedro Martinez
|
0.8797
|
21
|
|
Lagun Aro
|
Sito Alonso
|
0.8420
|
15
|
|
Unicaja Málaga
|
Joan Plaza
|
0.7874
|
23
|
|
Cai Zaragoza
|
José Luis Abós
|
0.5499
|
18
|
|
Joventut Badalona
|
Salva Maldonado
|
0.5406
|
15
|
|
F.C. Barcelona
|
Xavi Pascual
|
0.5268
|
26
|
|
CB Canarias
|
Alejandro Martínez
|
0.5215
|
13
|
|
Tuenti Movil Estudiantes
|
Txus Vidorreta
|
0.4956
|
12
|
|
Fuenlabrada
|
Chus Mateo/ Luis Casimiro
|
0.4494
|
12
|
|
Leche Rio Monbus
|
Moncho Fernández
|
0.3516
|
12
|
|
UCAM Murcia
|
Oscar Quintana/ Marcelo Nicola
|
0.3266
|
11
|
|
Laboral Kutxa
|
Sergio Scariolo
|
0.2299
|
18
|
|
La Bruixa d’Or Manresa
|
Borja Comenge/ Pere Romero
|
0.1492
|
7
|
|
C.B. Valladolid
|
Ricard Casas
|
0.1033
|
3
|
|
Bilbao Basket
|
Rafa Pueyo
|
0.0491
|
12
|
Analysis of the NBA coach of the year award
Análisis del entrenador del año en la NBA
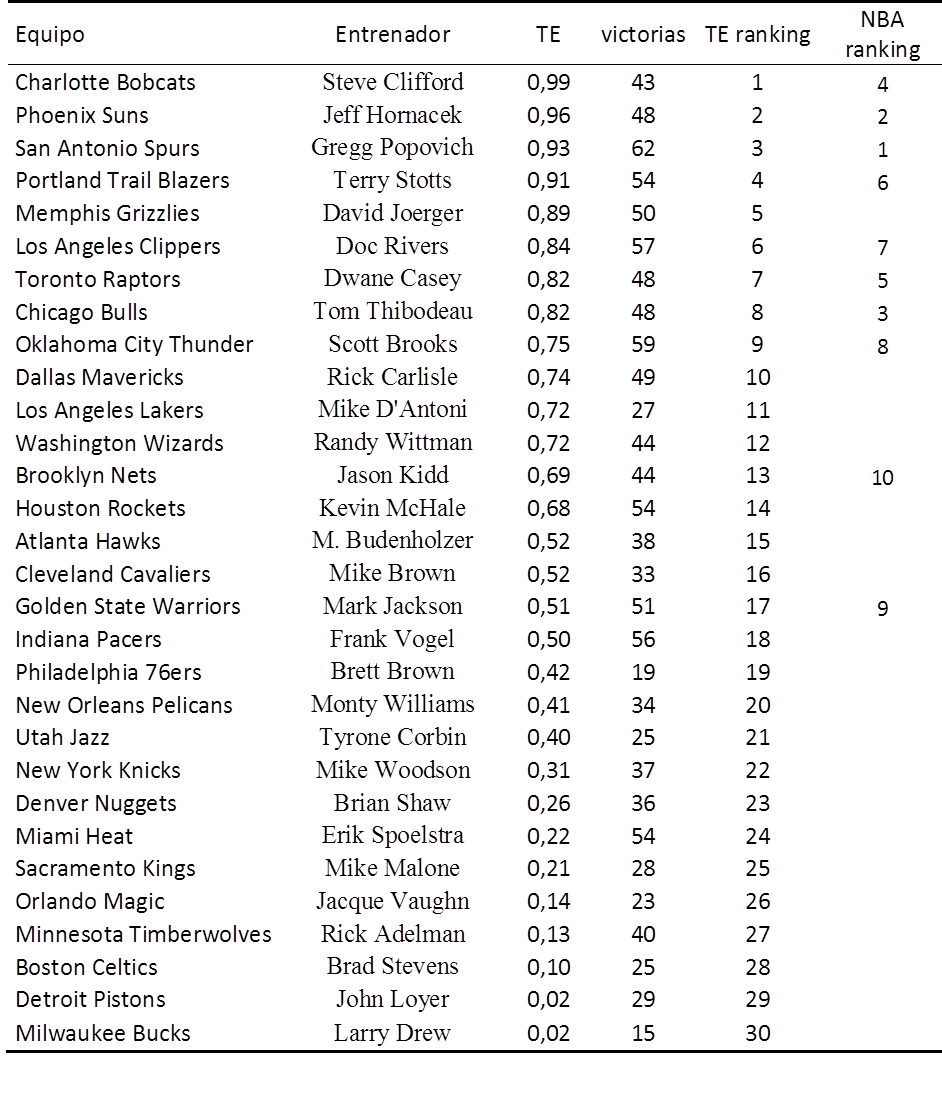
- De los 9 primeros entrenadores en el TE ranking sólo está ausente del ranking de la NBA el entrenador de los Memphis Grizzlies. Puede deberse que usando las cuotas se tiene en cuenta las lesiones de los jugadores y los Grizzlies han conseguido meterse en playoffs jugando muchos partidos sin uno de sus baluartes (Marc Gasol)
- Steve Clifford aparece en primera posición del ranking TE con cierta holgura pero sólo ocupa la cuarta posición en las votaciones de la NBA. Parece que obtener 43 victorias con un equipo como los Charlotte Bobcats tiene más mérito que ganar la liga con los San Antonio Spurs. Sin embargo, en el concurso de “popularidad” que supone el premio de entrenador del año de la NBA no sale todo lo bien que debería. Steve Clifford obtiene 127 puntos por los 380 del entrenador de los San Antonio Spurs o los 339 de Jeff Hornacek.
La distancia parece excesiva y puede que el no entrenar a un equipo potente o no haber sido jugador profesional como Jeff Hornacek hagan que obtenga menos votos. Esto desde luego no debería ser así. La metodología que yo empleo obviamente no es perfecta, pero si proporciona un ranking objetivo y por lo que se ve bastante sensato. Por lo que yo propongo que para los premios de mejor entrenador se dejen de usar votaciones y se empiecen a usar métodos objetivos donde el que yo propongo sería uno de ellos.
It does exist an objective alternative to the NBA coaches’ ranking provided by the ESPN.
Si, existe una alternativa objetiva al ranking de entrenadores de la NBA publicado en la web de ESPN
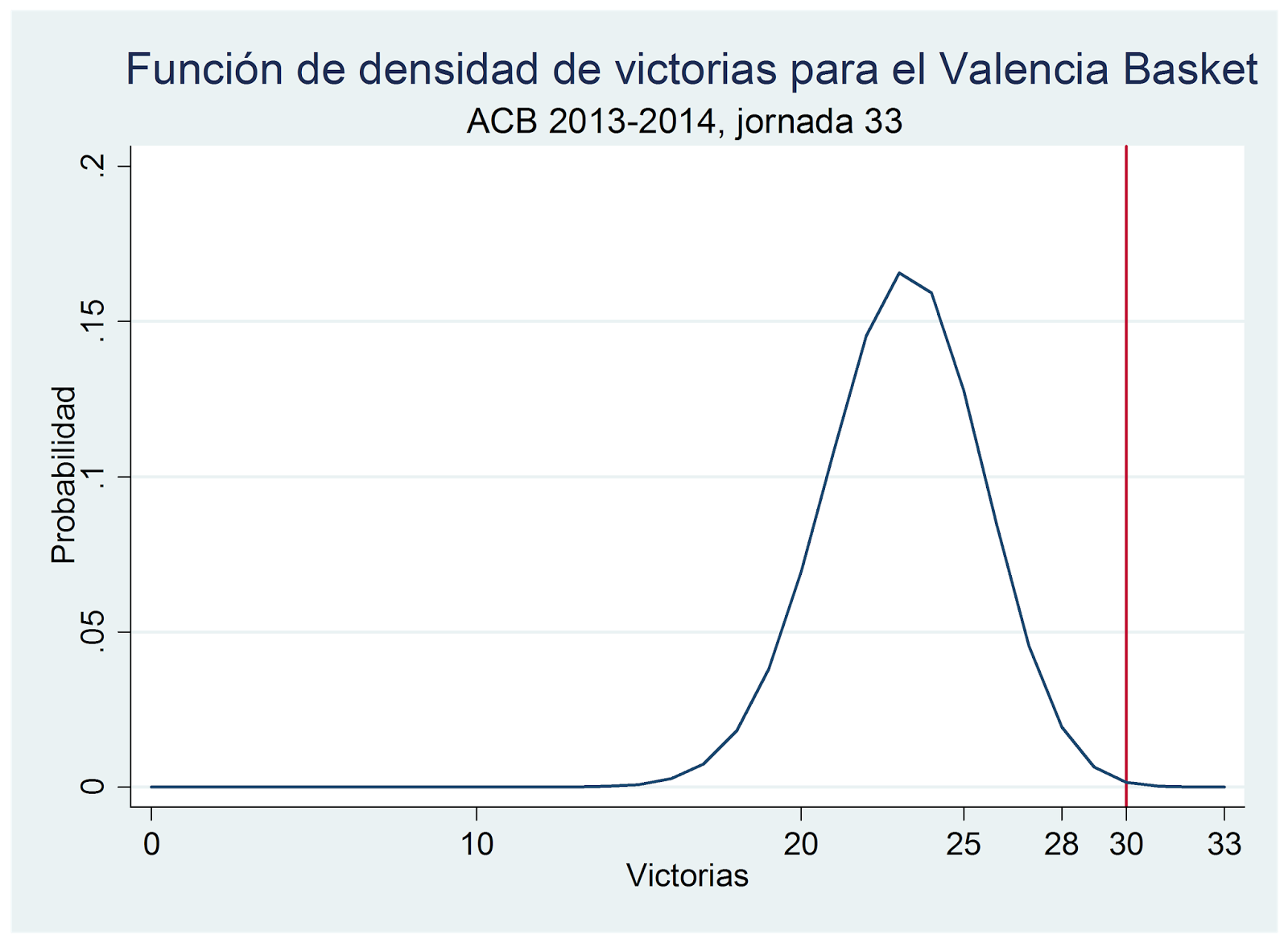
Como puede verse la probabilidad de haber obtenido un número mayor de victorias que las realmente obtenidas (36 hasta la jornada 74) es 2,71%. Entonces para calcular una medida objetiva del rendimiento del equipolo único que hay que hacer es calcular el inverso de ese 2,71% y su inverso da un rendimiento del 97,3%, o en términos de 0 a 10 un 9,73.
Como se puede observar en la tabla, los resultados difieren de manera considerable. En concreto, el coeficiente de correlación lineal entre nuestras puntuaciones y las de ESPN es del 63%, mientras que el coeficiente de correlación de rangos es del 68%.[1] Luego, la relación entre ambas puntuaciones es positiva pero no todo lo grande que debería ser.
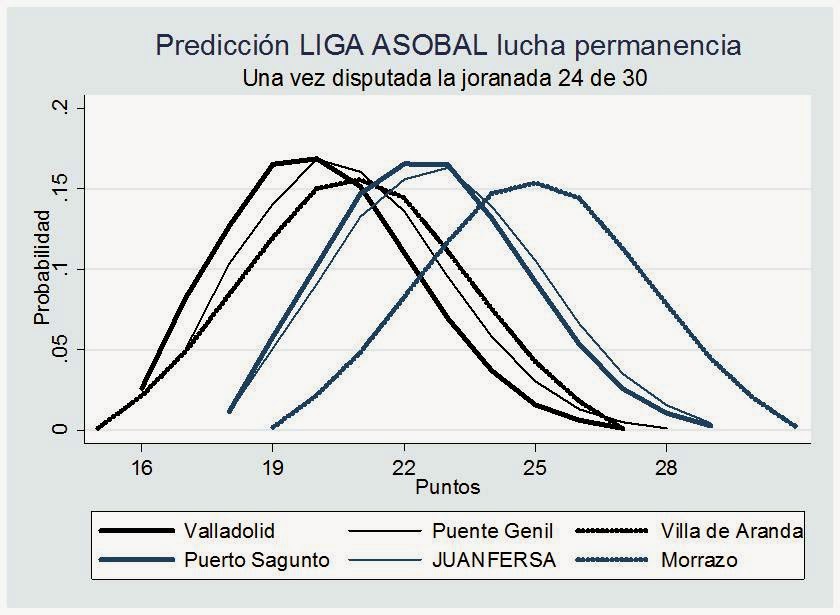
Predicciones para la zona de permanencia en la ASOBAL
|
jornada
|
local
|
visitante
|
Prob victoria local
|
Prob empate
|
Prob victoria vistante
|
|
25
|
BM Huesca
|
Valladolid
|
0.72
|
0.09
|
0.20
|
|
25
|
Cuenca
|
Morrazo
|
0.61
|
0.10
|
0.29
|
|
25
|
La Rioja
|
Genil
|
0.83
|
0.06
|
0.11
|
|
25
|
Pto Sagunto
|
Gijón
|
0.63
|
0.10
|
0.27
|
|
25
|
Villa Aranda
|
Irun
|
0.69
|
0.09
|
0.22
|
|
26
|
Gijón
|
BM Huesca
|
0.39
|
0.11
|
0.50
|
|
26
|
Granollers
|
Genil
|
0.81
|
0.07
|
0.12
|
|
26
|
Morrazo
|
Villa Aranda
|
0.64
|
0.10
|
0.26
|
|
26
|
Pto Sagunto
|
La Rioja
|
0.23
|
0.09
|
0.68
|
|
26
|
Valladolid
|
Barcelona
|
0.05
|
0.05
|
0.90
|
|
27
|
Ademar
|
Morrazo
|
0.62
|
0.10
|
0.28
|
|
27
|
Barcelona
|
Gijón
|
0.92
|
0.04
|
0.04
|
|
27
|
BM Huesca
|
Pto Sagunto
|
0.70
|
0.09
|
0.21
|
|
27
|
Cuenca
|
Valladolid
|
0.67
|
0.10
|
0.24
|
|
27
|
Genil
|
Anaitasuna
|
0.40
|
0.11
|
0.49
|
|
27
|
Villa Aranda
|
Aragon
|
0.47
|
0.11
|
0.42
|
|
28
|
Gijón
|
Cuenca
|
0.59
|
0.11
|
0.30
|
|
28
|
Irun
|
Genil
|
0.58
|
0.11
|
0.31
|
|
28
|
Morrazo
|
Guadalajara
|
0.52
|
0.11
|
0.37
|
|
28
|
Pto Sagunto
|
Barcelona
|
0.06
|
0.05
|
0.89
|
|
28
|
Valladolid
|
Villa Aranda
|
0.59
|
0.11
|
0.30
|
|
29
|
Ademar
|
Valladolid
|
0.74
|
0.08
|
0.17
|
|
29
|
Cuenca
|
Pto Sagunto
|
0.62
|
0.10
|
0.27
|
|
29
|
Genil
|
Morrazo
|
0.41
|
0.11
|
0.48
|
|
29
|
Villa Aranda
|
Gijon
|
0.57
|
0.11
|
0.32
|
|
30
|
Aragon
|
Genil
|
0.73
|
0.09
|
0.18
|
|
30
|
Gijón
|
Ademar
|
0.45
|
0.11
|
0.43
|
|
30
|
Morrazo
|
Granollers
|
0.45
|
0.11
|
0.44
|
|
30
|
Pto Sagunto
|
Villa Aranda
|
0.55
|
0.11
|
0.34
|
|
30
|
Valladolid
|
Guadalajara
|
0.45
|
0.11
|
0.44
|
El milagro del Atleti
Balance competitivo en la EHF Champions League
Donde se ve el gráfico promedio. En media hay dos equipos muy por encima del resto, normalmente hay 3 equipos intermedios y un último equipo con un nivel muy bajo como para participar en una competición como la actual EHF Champions League.
Competitive balance in the NBA
PS2: We would like to acknowledge Leigh Herdman of Herdman-Highton Consultancy Ltd for providing us the data
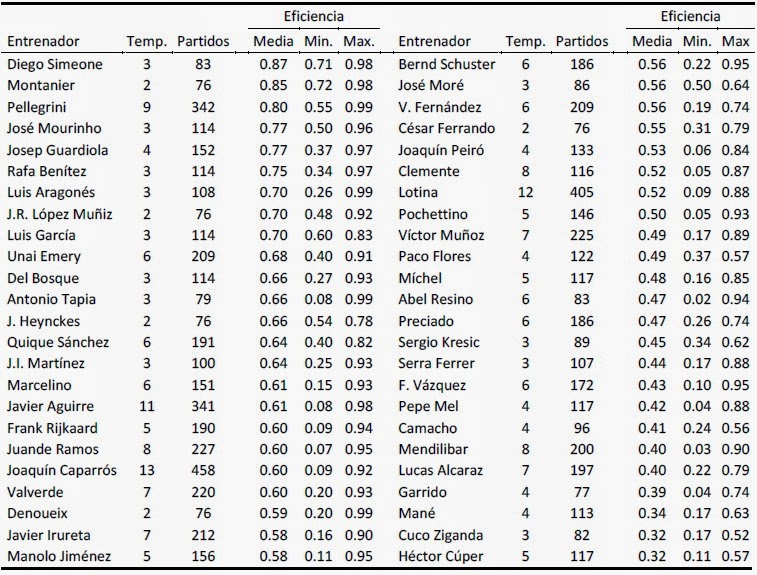
Eficiencia de los entrenadores en la liga BBVA 2000-2014
Una vez calculada estas funciones se puede calcular la probabilidad de que el número de puntos obtenido por un equipo sea igual o menor que un determinado número de puntos. Este valor puede verse como una medida de la eficiencia del entrenador, en el sentido que es la probabilidad de que un equipo entrenado por un entrenador hubiera obtenido menos o los mismos puntos que realmente obtuvo. Como es una probabilidad el valor se sitúa entre 0 y 1, cuánto más próximo esté este valor a 1 mejor habrá sido la actuación del entrenador.
La siguiente tabla muestra el promedio, mínimo y máximo de la eficiencia de cada entrenador para las distintas temporadas en las que actuaron. Los resultados más importantes indican que el entrenador más eficiente hasta la fecha ha sido Simeone seguido por Montanier. Hay que destacar que estos entrenadores aparecen con un número bajo de temporadas. Si nos fijamos en los entrenadores que hayan estado más de 5 temporadas, el entrenador más eficiente y con una diferencia muy importante ha sido Pellegrini, seguido por el muchas veces criticado pero que según estos resultados lo ha hecho bien en sus equipos Unai Emery. Destacar también que Mourinho y Guardiola consiguen una eficiencia promedio muy similar y muy alta.