Authors: Julio del Corral and Carlos Gómez-González
In January, Javier Ares, who is a well-known Spanish sport journalist wrote a tweet saying: “Is it just a coincidence that Chelsea and Liverpool (first qualified teams in Premier League) are not playing European competitions? The idea behind this question is reasonable because the teams that do not play European competitions can focus on the domestic league and obtain better results. For instance, Celta de Vigo was relegated to the second division while playing Champions League in the 2003-2004 season. This article shows that although some examples can point in this direction, statistical analyses shows the opposite during the period 2005-2016: the teams playing Champions League have a better performance in La Liga. However, the improvement is marginal when using advanced statistical models.
The database includes the following leagues: Belgium, Germany, England, France, Greece, Italy, the Netherlands, Portugal, Scotland, Spain and Turkey. The seasons analyzed go from the 2005-2006 to the 2015-2016.
In order to include a measure of performance in the league, this analysis uses the measure of efficiency published in del Corral, Gallardo, and Maroto (2017) in the Journal of Sports Economics, which can be downloaded in this link. This measure is calculated as the inverse of the probability of obtaining more points than the actual ones using betting odds data. Thus, the teams having a performance above expectations, e.g., Leicester in the 2015-2016 season, show values close to 1. Leicester obtained a value of 0,9998 in that season. In contrast, the teams having a performance below expectations, e.g., Mourinho’s Chelsea in the 2015-2016 season, show values close to 0. Chelsea had a coefficient of 0.021 (Further explanations and applications of this methodology can be found in the following links for the Spanish football: and for the basketball league ACB)
A first step is to compare the efficiency of the teams playing European competitions (any), or Champions League (group phase), and the teams playing the domestic leagues only.
| Observations | Efficiency | |
| Play Europe Champ. | 1,385 | 0.50 |
| Do not play Europe Champ. | 717 | 0.58 |
| Play Champions League | 1,843 | 0.51 |
| Do not play Champions League | 259 | 0.63 |
| Total | 2,102 | 0.52 |
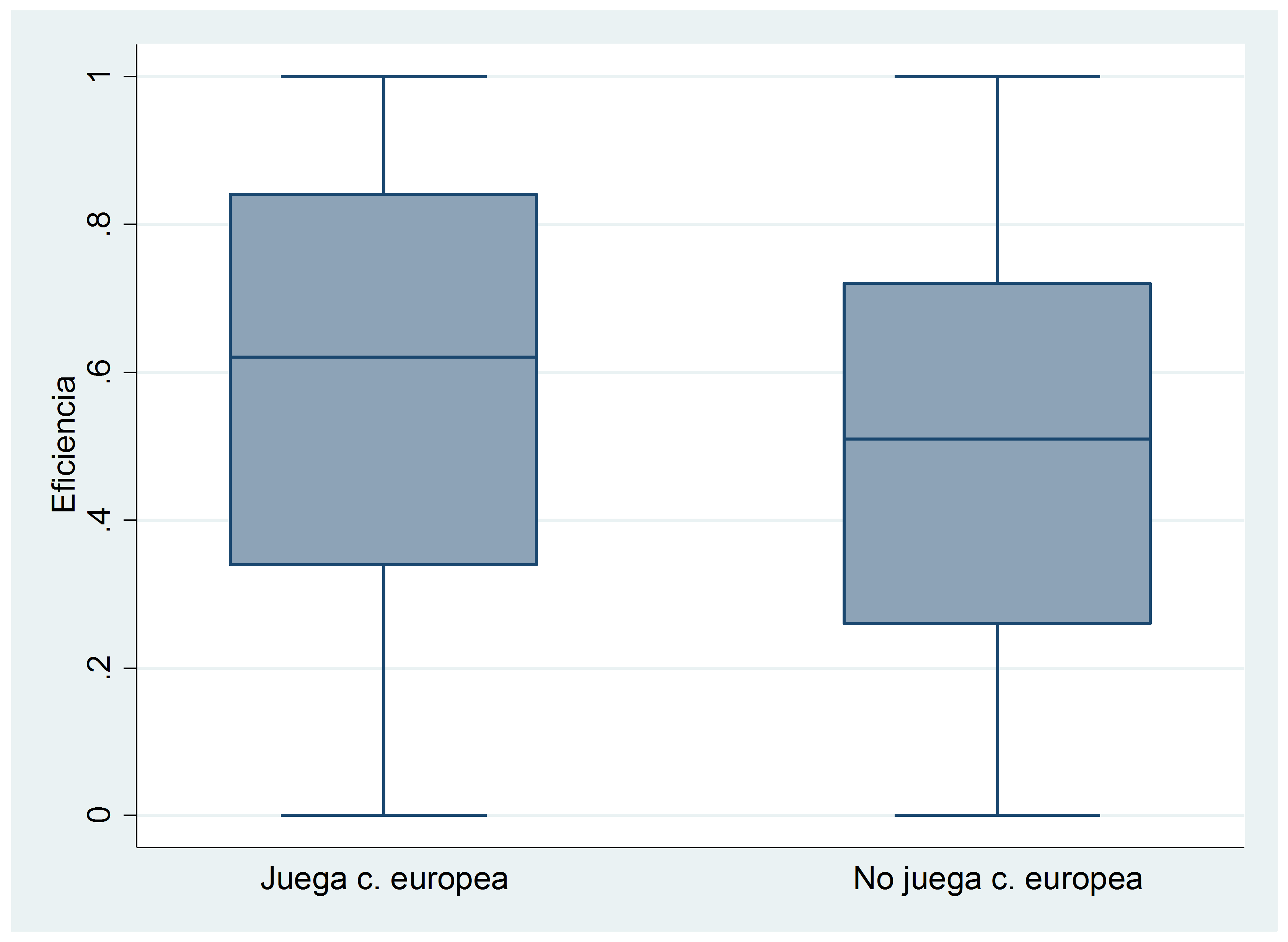
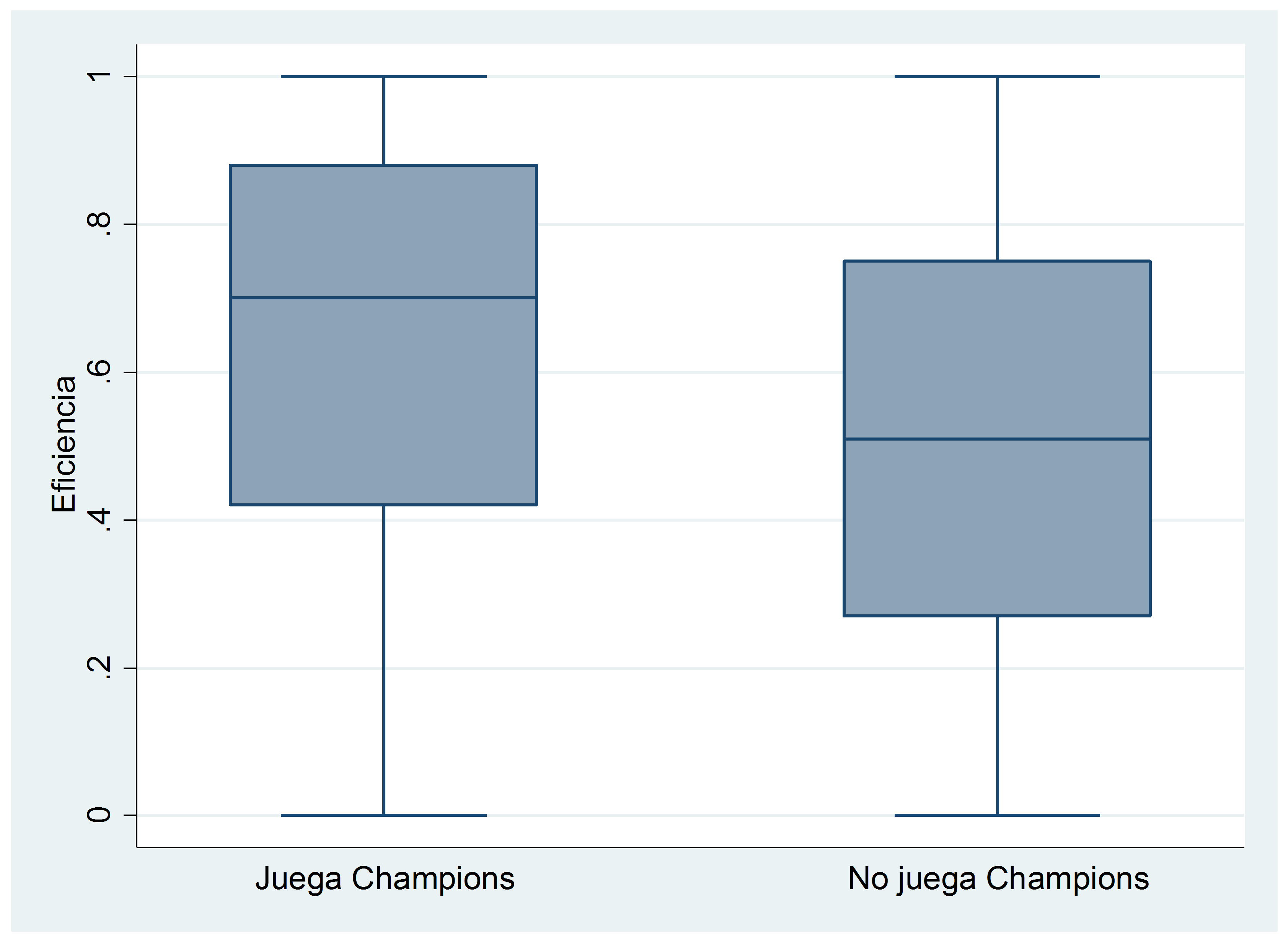
Please notice that the differences are statistically significant in both cases. The following box plots show graphically these differences, where the middle line is the median and the box represents the upper and lower quartiles.
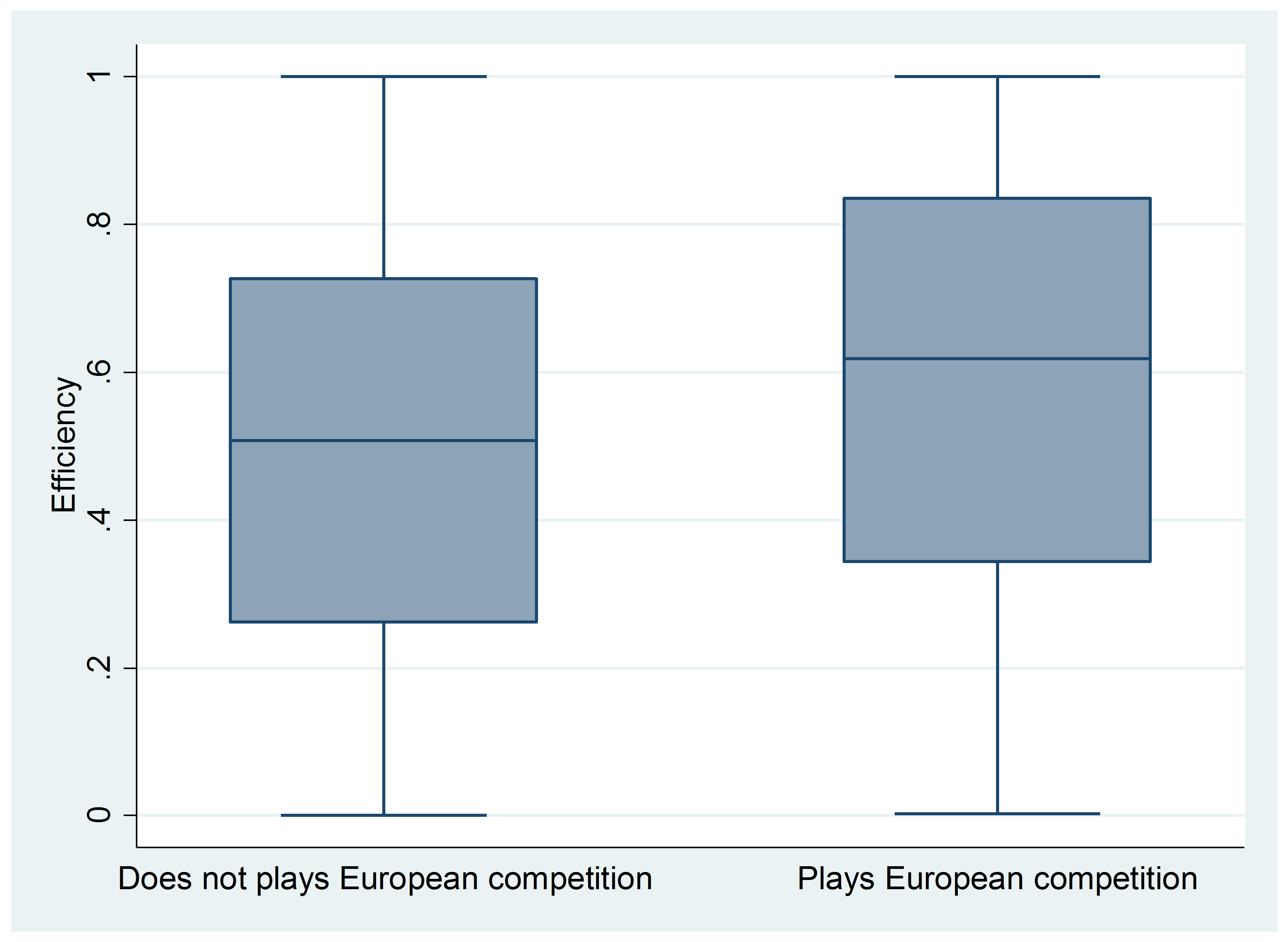
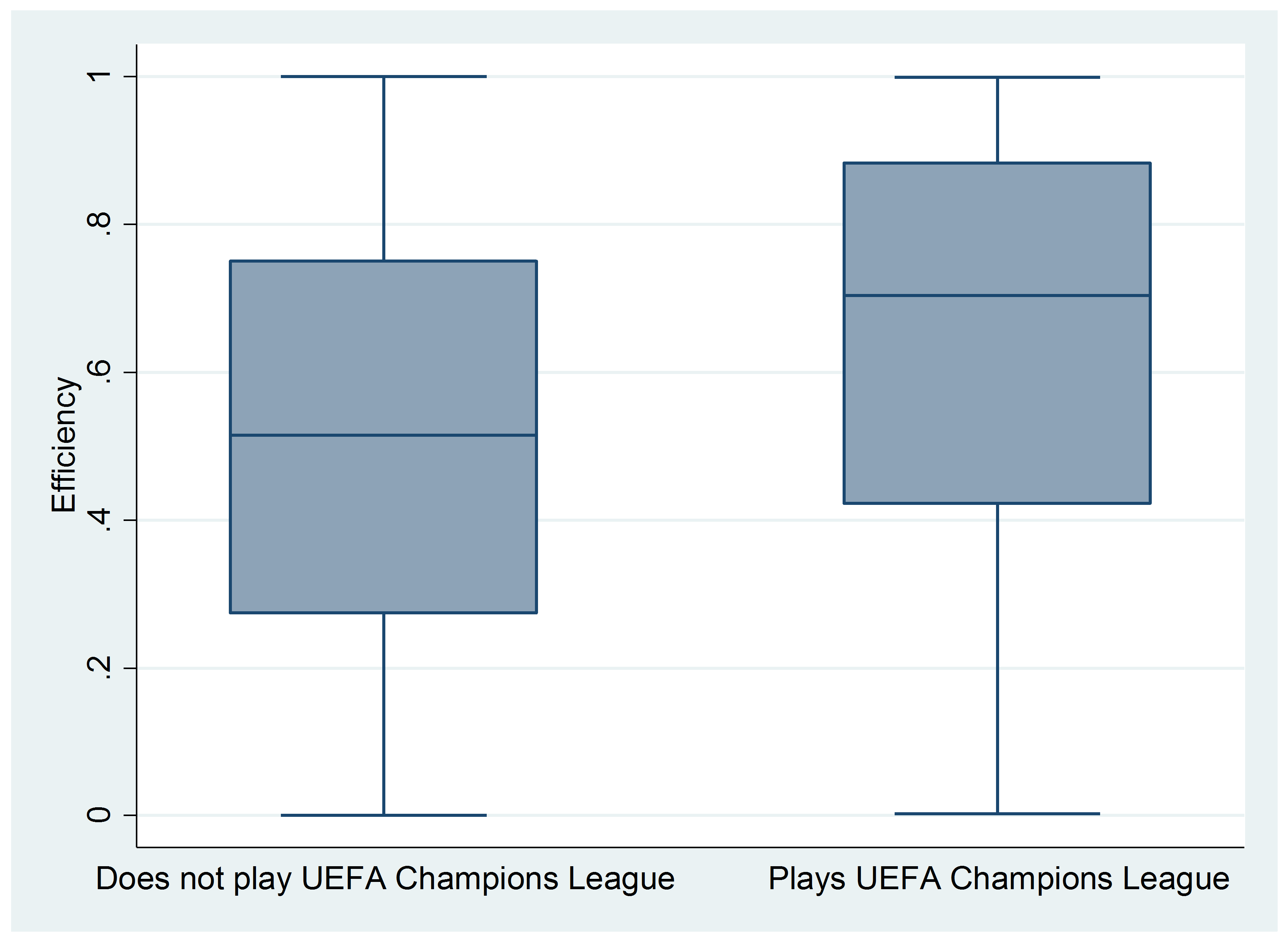
A complementary approach is to analyze the number of observations that are above and below the mean (0.52). Regarding the teams playing Champions League, 167 teams obtained higher efficiency values than the mean, while 92 were below. However, regarding teams that do not play Champions League, 906 teams obtained an efficiency above the mean, while 937 were below.
Thus, this preliminary analysis shows that playing European competitions is not counterproductive for performance in domestic leagues, but rather beneficial.
Nevertheless, impact evaluation techniques are necessary to better understand the real effect that the participation in Champions League has on teams’ performance. Specifically, the most similar team that do not participate in Champions League is used to match the team participating in Champions League. This would be the most similar team in terms of quality (using Transfermarkt values) from the same domestic league. In this case, some teams will never have an appropriate match. For example, a team that is similar to Real Madrid in terms of quality and do not play Champions League cannot be found in La Liga in the season 2015-2016. The difference between Real Madrid and the first best team that do not play Champions League is too much. In order to avoid this problem, the observations of teams that have played too many times in Champions League (ECL) are omitted. The results are as follows:
| Observations | Ef. team ECL | Ef. team no ECL | |
| Complete sample | 259 | 0,63 | 0,60 |
| Omit team 11 ECL | 215 | 0,63 | 0,60 |
| Omit team >9 ECL | 195 | 0,63 | 0,60 |
| Omit team >8 ECL | 177 | 0,61 | 0,59 |
| Omit team >7 ECL | 153 | 0,60 | 0,60 |
In fact, when the methodology of the most similar neighbor is implemented, the effect of the policy (to participate) in Champions League is 0.003. Therefore, participating in Champions League does not have neither a negative nor a positive effect on the efficiency in the domestic league.
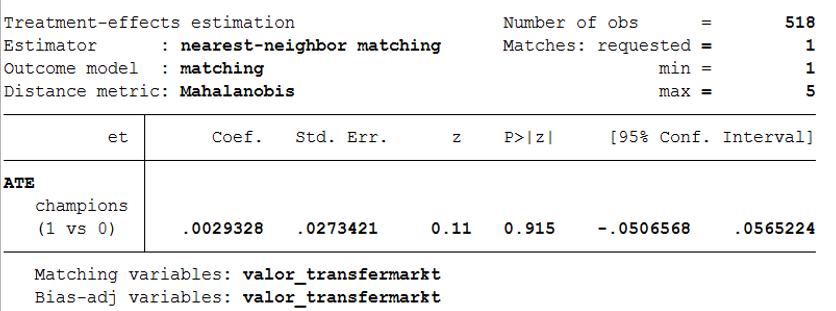
In short, it is believed that participating in European competitions is counterproductive for the performance of teams in the domestic leagues. However, the evidence suggests that if any, the effect is positive. Therefore, supporters of teams qualified for Champions League (Sevilla, hopefully) can sleep peacefully as the participation in Champions League will not directly affect the performance in the league.