Categoría: Artículos Interesantes

Mayor comprensión de los diversos mecanismos de formación de superficies hidrofóbicas.

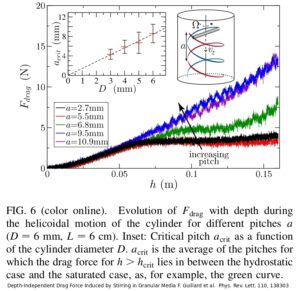
En un artículo reciente, unos investigadores han logrado medir con mayor precisión la tensión generada en una gota sobre tres tipos de superficies hidrofóbicas, esto es, que repelen los líquidos en su superficie, logrando confirmaciones experimentales de modelos sobre la tensión ejercida por la gota con la superficie en movimiento.

Esta medida es importante porque la tensión producida sobre la hoja «desfavorece» el movimiento. Es decir, cuanto más pequeña sea, más hidrofóbica es una superficie. Y además, saber cómo se comporta con la velocidad relativa del fluido sobre la superficie es fundamental si quieres calcular, o estimar, el rozamiento del fluido en la superficie. Y hasta ahora nadie había logrado observar las diferencias entre las diversas superficies hidrofóbicas con tanto nivel de detalle.

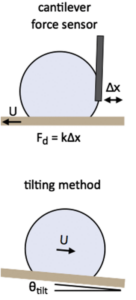
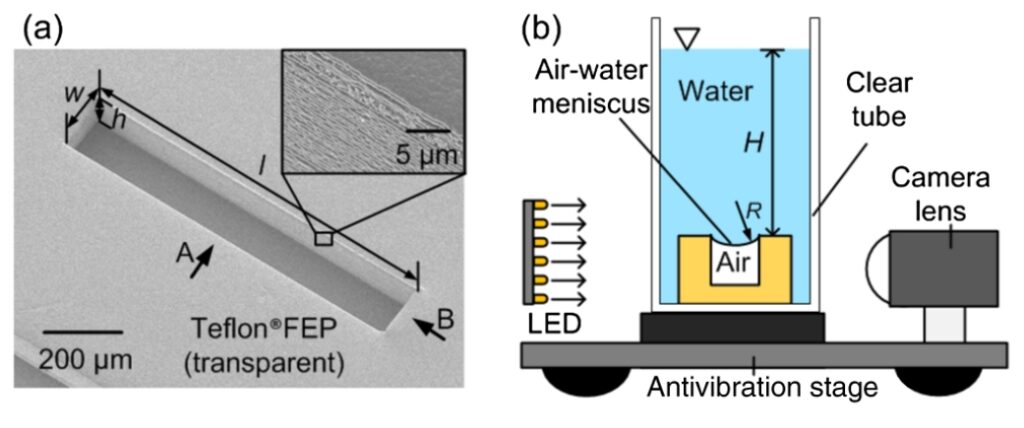
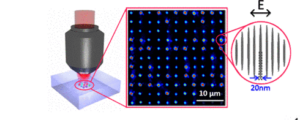
Figura 01. Del artículo PHYSICAL REVIEW LETTERS 120, 244503 (2018)

Como indican en el artículo, una de las claves está en el método que tienen para poder medir las fuerzas. Como cualquier idea genial, es simplísima una vez que se cuenta, pero muy difícil de darse cuenta y de hacer: Usan un «cantilever», que parece ser se traduce por guía voladiza, pegada a la gota. Es decir, una finísima barra de cristal, concretamente un tubo capilar, se acerca con cuidad extremo a la gota del líquido sobre la superficie para poder medir la flexión en el tubo de cristal, y por aplicación directa de la ley de Hooke ( F = k Δx ) sacan del desplazamiento la fuerza, fijaos en la figura 1. La otra opción genial es deslizarla  un ángulo determinado y comprobar su dinámica en el tiempo, su x(t), que es muy distinta según la gota esté sometida o no a una fuerza constante o a ninguna fuerza.

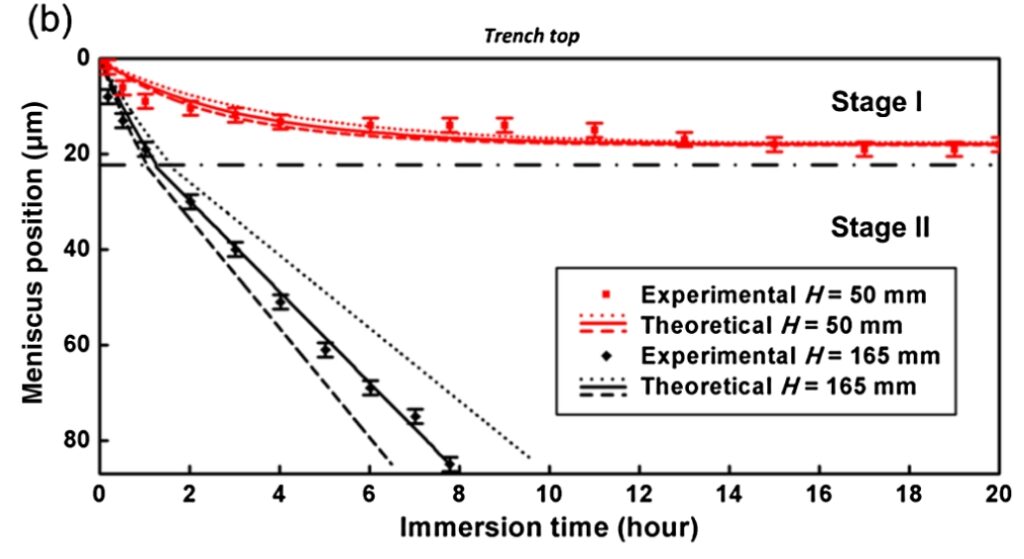
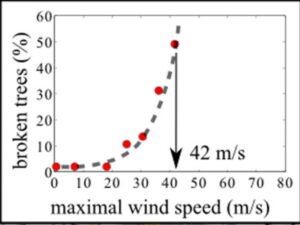
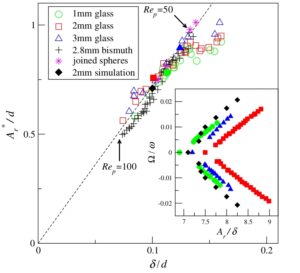
Con el segundo método se obtiene la segunda figura, donde los desplazamientos a lo largo del tiempo evidencian las fuerzas a las que se somete la gota por la superficie en la que se desliza.

Figura 02. x(t) para las tres superficies estudiadas. Del artículo PHYSICAL REVIEW LETTERS 120, 244503 (2018)

Las tres superficies hidrofóbicas estudiadas son las más comunes:

  • Una superficie conformada con pilares nanométricos para atrapar el aire y generar menos arrastre de la gota,
  • Una superficie con «cepillos moleculares», que debido a las proteínas que forman la superficie impiden el paso del líquido y
  • Una superficie lubricada con un aceite, lo que provoca un mayor deslizamiento de la gota del agua por la superficie.
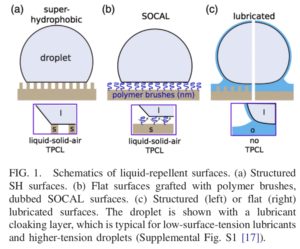
Los tres tipos de superficies hidrofóbicas estudiadas en el artículo.
De PHYSICAL REVIEW LETTERS 120, 244503 (2018)

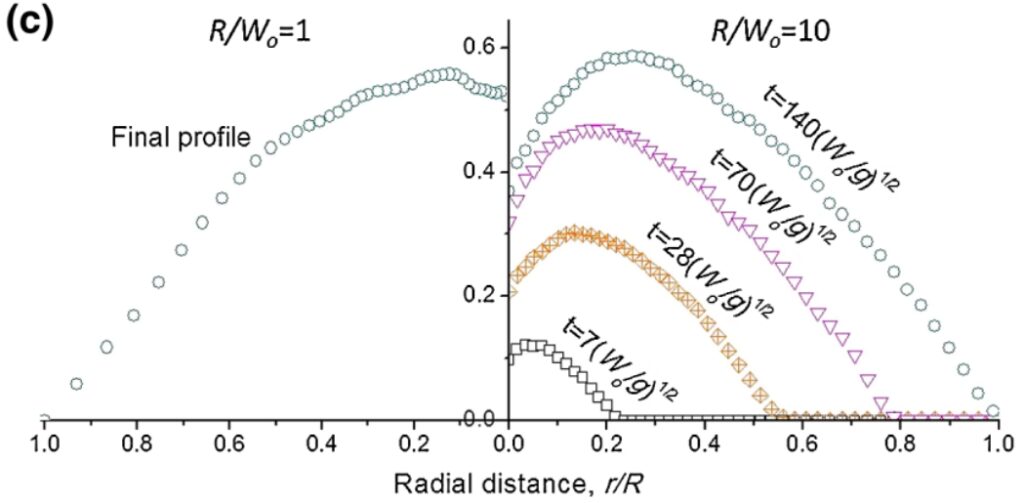
La figura 03 muestra un ejemplo de los tres tipos de superficies. El artículo original está aquí, y salió publicado en la revista Physical Review Letters.

Superficies hidrofóbicas que aguanten sumergidas

Uno de los mayores problemas del transporte de líquidos en general y del transporte en líquidos, es decir, del transporte marítimo, es el alto rozamiento del fluido en estado líquido. De hecho, al transportar líquido por una tubería existe el problema de que una parte importante de la energía que se le proporciona al fluido se tiene que emplear en eliminar el rozamiento del líquido con la tubería que lo transporta.

En ambos casos una solución muy elegante consiste en colocar un fluido en estado gas entre el líquido que se mueve y la superficie sólida contra la que se mueve. Entonces, el rozamiento desciende muchísimo porque lo que roza es el sólido contra un gas y un gas contra un líquido. El problema es «sujetar» el gas cerca del sólido. El muy desgraciado del gas tiene a escaparse hacia el líquido, promoviendo de nuevo ese contacto líquido-sólido que sería deseable evitar.

Una forma de mantener el gas cerca de la superficie sólida es el uso de cavidades de tamaño nanométrico, donde en principio el gas se queda algo más de tiempo. El problema es que al moverse el líquido respecto a la superficie, y simplemente por la presión del líquido, se acaba llenando de líquido la nanocavidad con gas. Hasta ahora, si ahora es el 2014, claro. En el artículo PRL-vol113-136103(2014) se presenta un modelo capaz de predecir si el aire (gas empleado) se quedará atrapado en la ranura empleada o no. Y se demuestra que el modelo es válido con una ranura real.

Según el modelo que se presenta en el artículo, la clave para lograr que una ranura «atrape» aire por un tiempo indefinido (más de 50 días en el experimento) es la altura que el agua, o líquido, tiene sobre la ranura, de forma que hay un altura crítica a partir de la cual se moja la ranura.  Las buenas noticias son que esa altura crítica depende de la anchura de la ranura, las malas que la altura crítica máxima es del orden de los centímetros, lo que dado que un barco se sumerge metros, implica que el uso de estos sistemas para evitar rozamiento queda descartado.

Sin embargo, es un gran experimento que creo interesante reseñar porque presenta datos y modelos sencillos y elegantes para entender un problema muy complejo. La esencia de la física bien hecha. El montaje experimental es el de la figura siguiente:

Montaje experimental. Artículo PRL-Vol311-136103(2014)

La figura de la izquierda muestra una ranura con las dimensiones y convenciones empleadas en el artículo, mientras que en la derecha se observa un esquema del sistema experimental. Con este montaje experimental, observar si la ranura se moja o no es cuestión de explorar imágenes proporcionadas por una cámara ajustada a la lente de la figura anterior, con lo que se obtienen gráficas como la siguiente, donde se muestra lo que pasa con altura de líquido por debajo de la crítica, es decir, con el aire atrapado de manera estable y con una altura por encima de ese valor, lo que implica que el aire no permanece en la ranura:

Permanencia o no del aire en la ranura. Artículo PRL-Vol311-136103(2014)

La forma de medir si hay aire o no es mediante la posición del menisco que se forma en la ranura. La gráfica presenta la distancia máxima de ese menisco desde el comienzo de la ranura hasta su fondo. Cuando llega a unos 80 micras, llega al fondo de la ranura. Fíjense que cuando al altura del agua es superior a la crítica, la ranura se moja, esto es, se vacía de aire en «sólo» ocho horas, mientras que para una altura de agua por debajo de la crítica, la ranura permanece indefinidamente llena de aire. Observen además la fantástica coincidencia entre el modelo y los datos experimentales, que indica que el modelo acierta en sus predicciones.

Para hacer montañas de granos, es importante saber cómo se formó la montaña.

A lo mejor no parece importante, pero un auténtico misterio de la física hasta hace poco era la formación de montones con material granular en caída libre. Es decir, yo dejo caer desde una distancia fija algo en forma granular, y trato de predecir o modelar la forma que tendrá ese montón.  Hasta hace algún tiempo había resultados experimentales y teóricos contradictorios, entre otras cosas porque no hay un modelo claro de material granular: El material granular son pequeñas piezas con formas distintas entre sí y no se sabe muy bien cómo modelar ni la forma del grano, ni la interacción entre ellos.

Piensen que el material en forma granular tiene interacciones entre granos o partículas vecinas que los separa del sólido rígido, que es el equivalente a granos formando un auténtico continuo, como en los metales, y del modelo de partículas rígidas separadas, cuando no hay demasiados granos. Un modelo que daba algún resultado decente es adaptar el modelo de sólido deformable y quizás elástico con propiedades constitutivas propias para el material granular. Es decir, se hace una aproximación de un material en estado discreto por un continuo cuya descripción encaja en los experimentos con diversos materiales granulares.

Este tipo de aproximaciones no ha sido capaz de resolver un problema de la generación de montones: que la distribución de presiones en el centro del montón depende de cómo se haya formado el montón, de forma que si se genera desde un sólo punto de caída del material, aparece una depresión en la base del montón; cuando se genera median una «lluvia», es decir desde múltiples puntos de caída del material, la depresión en el centro no es visible. En el artículo PRL – Vol113 – 068001 (2014) se demuestra que el uso de modelos elastoplásticos que no eran capaces de predecir estos dos resultados sí que funcionan, pero si se usa un modelo matemático que tiene en cuenta la historia del fenómeno para la descripción numérica.

Cuando se simula un sistema tridimensional en un ordenador, hay que hacer una malla tridimensional de puntos en la que se calculan las propiedades del material, presión, densidad, fuerzas, etc. Esta malla puede seguir o no al material en su movimiento. Cuando la malla es fija y el material se mueve dentro de ella, podemos tener en cuanta la historia de este movimiento mejor.

El resultado final es que en simulaciones con dos modelos distintos de materiales elastoplásticos, se observa la caída de presión en le centro de la pila o montón que ya fue observada experimentalmente, como la figura tres del artículo muestra:

Perfiles de presión de pilas de material granular. Del artículo PRL-Vol311-0068001 (2014), figura 3.

En la figura se muestran los perfiles de presión según el material granular caiga en forma de «lluvia», izquierda, o desde un punto, derecha. Ambos están marcados por la relación entre el ancho de la boca y el radio del montón. En el primer caso, R/W0 es 1. Cuando R/Wo es 10, es decir, todo el material cae desde un sólo punto, se puede observar como según el instante de tiempo en el que observemos el perfil de presiones, éste cambia y termina desarrollando la depresión central al final.

 

Sistema de almacenamiento eterno (O algo parecido)

Se ha encontrado un sistema de almacenamiento que resiste el paso del tiempo, puesto que dura más o menos lo que dura el universo, usando los sistemas de estimación de tiempo generalmente aceptados como razonables.

Decaimiento con el tiempo a temperatura fija del material. Del artículo Phys. Rev. Lett. 112, 033901 (Gráfica de Arrhenius)

 

Al menos, a muy bajas temperaturas. Fíjense en la gráfica, donde los puntos rojos son extrapolaciones de las medidas señaladas con los rombos.
A temperaturas más altas, unos 190 grados centígrados(los 462 K de la gráfica), «sólo» dura más menos unos 10⁹ años…

Se basa en hacer marcas nanométricas en un vidrio: Con un láser muy rápido, para modificar la estructura del vidrio lo menos posible, se generan pequeñas (¡de tamaño nanométrico!) esferas que se «leen» mediante el uso de otro láser del mismo tipo, pero con mucha menos intensidad. Por supuesto, no se puede ni borrar ni alterar la información escrita en el cubo, pero es impresionante. Entre otras cosas, permite el almacenamiento tridimensional de información para, esencialmente, siempre.

Del artículo Phys. Rev. Lett. 112, 033901

Esta imagen muestre un esquema muy simplificado del proceso, con las dimensiones finales de los puntos generados por el láser.

En muchos libros de ciencia ficción se consideraban sistemas similares, como en las películas y libros de Superman, donde su nave traía cristales de información de su planeta Kripton.

El artículo original está disponible en este enlace.

Los árboles se rompen todos igual con el viento.

En un artículo de principios del año pasado publicado en la Physical Review E se soluciona una discrepancia de siglos (no exagero) sobre el escalado de la resistencia de los árboles a la tensión.

No quiero entrar en detalles, pero en principio la resistencia a la rotura de un árbol puede modelarse como la resistencia de un cilindro sólido a la rotura por doblado en un extremo, con el otro firmemente sujeto. Con este modelo, se puede estudiar experimentalmente la rotura en modelos a escala como se ve en la imagen siguiente, sacada del artículo anterior.

Al realizar esos estudios, una parte importante de las conclusiones es si hay alguna ley de escala que permita aplicar lo visto en el laboratorio en escalas de centímetros o milímetros a las escalas de los troncos delos árboles, de metros. Y no sólo la hay, sino que puede ser deducida. Y ese es el valor de esta investigación: es capaz de predecir cómo se rompe la barra de madera, y por lo tanto la velocidad de viento máxima que es capaz de soportar.

Los datos sobre el escalado, resumidos en la figura siguiente, son francamente sorprendentes por lo bien que se ajustan a la escala logarítmica.


Aunque no se aprecia en el recorte que he hecho, el eje vertical es el radio crítico de rotura respecto la longitud total del cilindro, mientras que el eje horizontal es la relación que predice el valor de la fracción anterior.
Se puede observar que para dos materiales bastante distintos, como son la madera y el grafito de las minas de los portaminas, la ley se mantiene.

Con estos resultados, los autores del artículo trataron de predecir un valor de la velocidad de viento máximo que un árbol puede soportar, y encontraron que estaba en torno a los 40 m/s para vientos no estacionarios, los más normales en una tormenta. En la figura siguiente se observa el porcentaje de árboles rotos en función de la velocidad media del viento durante una tormenta de enero de 2009, la llamada Klaus. Se comprueba un valor de más del 50% cuando la velocidad del viento pasa de 42 m/s.
¡No está mal para un modelo que considera un árbol como un cilindro sólido!

Impresión de estructuras metálicas con tintas hechas de óxidos.

La fabricación aditiva (o menos pomposamente, la impresión en 3-D) está recién despegando en el ámbito industrial, con aplicaciones muy impactantes, como la construcción de parte de las toberas de los cohetes de Space-x, o similares. Uno de los mayores problemas para su adopción por otras industrias está en su alto coste, que sólo lo justifica en casos muy excepcionales. Si se pudiera usar algún tipo de tinta para crear la forma, y luego pasarla por un horno, el proceso de fabricación se simplificaría y abarataría mucho, además de integrarse con mucha facilidad en procesos industriales conocidos.

Y ya se puede. En un artículo publicado recientemente, se demuestra el empleo de una «tinta» basada en PLA (un plástico empleado en impresoras 3-D convencionales) con óxidos de metales en suspensión que puede imprimir todo tipo de estructuras con óxidos metálicos, que luego se pueden transformar en metales usando hornos. Los resultados son espectaculares:

fig-04

Fíjense que en que las formas se hacen primero con el óxido, que luego exige un tratamiento térmico posterior para retirar el plástico y «desoxidar» (el término más correcto es reducir…) el óxido de metal. La aplicación que los autores de esta investigación proponen es su uso en la impresión de sistemas catalíticos para coches, tanto por costo del sistema tradicional como por la cantidad de material que se precisa.

Generación de metanol directamente usando CO2 del aire

Uno de los problemas más importantes a los que la especia humana está sometiéndose a sí misma y al planeta es el cambio del equilibrio climático que existía previo a la explosión de la población humana de los siglos XIX y XX. Gran parte de este cambio de equilibrio se debe a la emisión de una gran cantidad de gas CO2 a la atmósfera, doblando su concentración atmosférica en los últimos decenios respecto a los valores preindustriales. Para minimizar los efectos de este cambio de equilibrio en la especie humana y el planeta, porque ya es muy tarde para evitarlo por completo, una estrategia consiste en emitir menos cantidad del gas, y otra en hacer que la propia economía humana se encargue de generar usos extra para el CO2 atmosférico y, así, «gastar» más de ese gas para reducir su concentración en la atmósfera.

Para ello, se puede pensar en sintetizar elementos útiles que precisen CO2. Uno de ellos es el metanol, que es un precursor químico de muchísimos elementos importantes, además de ser un combustible relativamente bueno. Pues recientemente, se ha logrado la śintesis de metanol desde CO2 de aire atmosférico directamente. Es un avance muy importante, porque al emplear directamente el aire más energía que puede ser extraída de fuentes renovables y suponiendo que el mñetodo pueda escalarse a sistemas más grandes, se podría emplear para usar el carbono contenido en el dióxido de carbono atmosférico en un nuevo «ciclo de carbono» artificial, que se añadiría al natural. Esto reduciría la cantida de CO2 en la atmósfera, de manera que efectivamente contribuiríamos a «enfriar» el planeta.

Artículo original: Conversion of CO2 from Air into Methanol Using a Polyamine and a Homogeneous Ruthenium Catalyst

La gravedad es independiente del spin.

Revisando los correos con las últimas publicaciones, me llamó la atención un artículo escrito por gente de un laboratorio de China sobre la gravedad y la falta de influencia del spin sobre ella(1).

Pero antes de comentar los resultados, quiero hacer una pequeña introducción, basada en el artículo y lo que yo recuerdo y entiendo según la física que estudié. La relatividad general establece una serie de principios fundamentales, mensurables sobre el Universo, teóricamente válidos a cualquier escala espacial o temporal. Uno de ellos, el objeto de este artículo, es que la gravedad actúa dependiendo del movimiento de la partícula y de su masa, sin necesitar o tener en cuenta otros parámetros, como carga eléctrica, etc. Pero algunas teorías de mecánica cuántica establecen que el spin del sistema en observación afecta a la gravedad. Poco, pero de manera mensurable. ¿Y qué es el spin de un sistema físico? Pues resumiendo y simplificando muchísimo, una medida de la importancia del campo magnético en la dinámica de ese sistema. Es decir, cuanto más grande sea el spin, más se verá afectado el movimiento por un campo magnético(2).

Para comprobar si estas teorías son ciertas, «basta» con dejar caer dos sistemas físicos idénticos en todo excepto el spin y medir la diferencia de la gravedad en ambos casos. Y eso es lo que hicieron en este experimento con átomos de Rubidio 78, con los resultados de la siguiente gráfica:

Rb78-gravedad
(Del artículo: http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.117.023001)
En ella, se puede observar la diferencia en el valor de la constante gravitatoria según el valor del spin de los átomos, que vá de 1 a -1, y se observa un claro 0. Es la segunda gráfica, la marcada como b. La primera parte de la gráfica muestra los mismos datos antes de eliminar un error sistemático debido al campo magnético.

La verdad es que el artículo me pareció fascinante y creo que vale la pena compartirlo aquí.

(1) Artículo en la Physical Review Letters
(2) En la wikipedia hay una explicación más larga y prolija

Hacer agujeros con menos torque en materiales granulares.

Resulta que se ha demostrado experimentalmente que la fuerza ejercida sobre un cilindro rotando sumergido en un medio granular es independiente de la altura del material granular que esté encima del cilindro bajo determinadas condiciones experimentales.

Esto es muy interesante, porque lo que se esperaba es que fuera un fenómeno completamente hidrodinámico, lo que quiere decir que el material granular se comporta casi como si fuera un fluido. si eso es cierto, entonces la cantidad de fluido por encima de cilindro tiene una influencia clara en la presión que se ejerce sobre el cilindro, al «pesar» el material sobre el cilindro sumergido.

Pero resulta que si se hace rotar el cilindro lo suficientemente despacio, el cilindro crea una especie de «cueva», un hueco en el material granular, que provoca que el movimiento del cilindro sea independiente de la altura del medio granular que está por encima. Esto es muy interesante, porque quiere decir que si se desea hacer un agujero en un medio granular, si se rota en taladro lo suficientemente despacio, no hay que hacer tanta fuerza. El motivo es que al no depender la fuerza ejercida sobre el cilindro de la altura de medio por encima, esencialmente se reduce y hace constante el valor de esa fuerza.

Para poder hacer las mediciones utilizaron un sistema muy ingenioso: Mantuvieron fijo el cilindro sumergido en el medio granular y rotaron el contenedor del medio granular, mirar el esquema:

Torque-esquema

Y la siguiente imagen muestra como el torque disminuye mucho si se trabaja lo suficientemente despacio:

Torque-Variacion

Esto es muy interesante no sólo por la física que tiene detrás, sino también porque abre la puerta (de mi imaginación, al menos) a sistemas capaces de taladrar cuerpos celestes compuestos por polvos agregados, al menos superficialmente, con mucha menos potencia y esfuerzo, lo que es importantísimo en misiones espaciales, donde cada gramo de más es muy difícil de justificar.

Enlace al artículo: http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.110.138303

Esferas que flotan ingrávidas en gravedad.

Aunque pueda parecer paradójico, leyendo los artículos científicos que tengo por leer, eso es lo que me encontré.

Resulta que en un artículo publicado en el 2013, Esferas flotantes se les ocurrió un sistema muy interesante para poder observar qué pasa en dos esferas sumergidas en un líquido que no están sujetas a la acción de la gravedad: Usar un campo magnéticoa casi paraleelo y que las esferas sean sensibles a los campos magnéticos.

Con este sistema, pudieron observar el movimiento del fluido alrededor de las esferas, y vieron como su comportamiento dependía exclusivamente de magnitudes hidrodinámicas, sin necesitar para poder entenderlo ningún tipo de campo magnético.

La imagen de abajo es la muestra de una foto tomada con alta exposición y partículas de bismuto, el material de las esferas, para visualizar el flujo. Los colores son un añadido para observar el flujo con más claridad, que según simulaciones realizadas en las mismas condiciones, producen las líneas de flujo negras sobre impuestas sobre las trazas blancas, las líneas experimentales. Las flechas indican las direcciones del flujo.

Esferas-01
Figura 2 del artículo Spontaneous Orbiting of Two Spheres Levitated in a Vibrated Liquid H. A. Pacheco-Martinez, L. Liao, R. J. A. Hill, Michael R. Swift, and R. M. Bowley Phys. Rev. Lett. 110, 154501

Además, como es un movimiento puramente hidrodinámico, pudieron hacer colapsar varios datos del movimiento en una sola gráfica adimensional, que es la siguiente:

Acel. adim. en esferas
Figura 1 del artículo Spontaneous Orbiting of Two Spheres Levitated in a Vibrated Liquid H. A. Pacheco-Martinez, L. Liao, R. J. A. Hill, Michael R. Swift, and R. M. Bowley Phys. Rev. Lett. 110, 154501

Las unidades escogidas son la amplitud respecto al medio en reposo adimensionalizada con el diámetro del contedor, Ar/d,y la longitud de penetración viscosa, otra manera de colocar la viscosidad y relacioanrla con la frecuencia.

Me pareció muy interesante por dos razones:

  • Es un uso claro de números adimensionales adecuados al sistema hidrodinámico y
  • La manera de «eliminar» la gravedad contrarrestándola con una fuerza magnética me parece particularmente elegante.