Blog

Publicado el

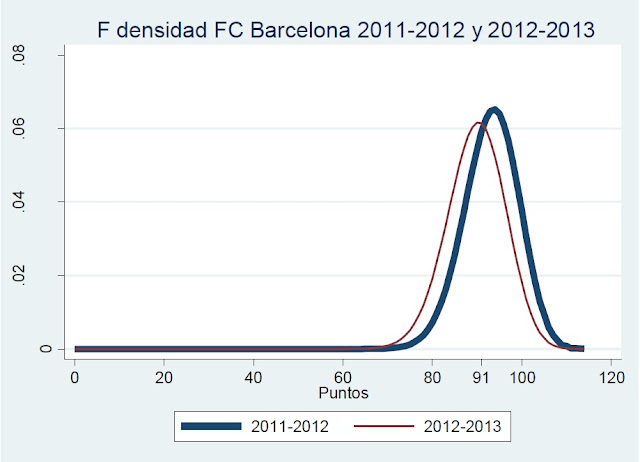
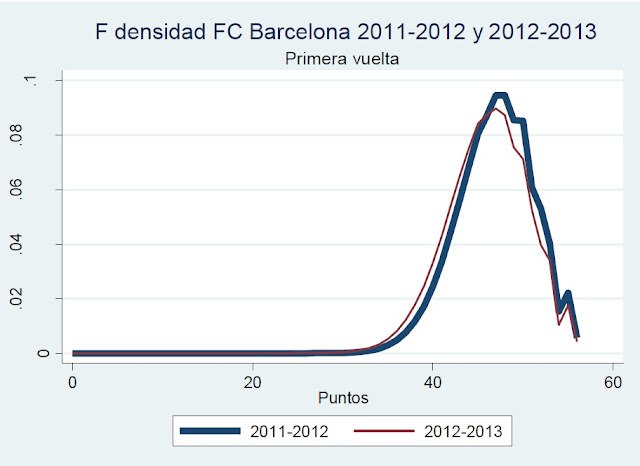
¿Es realmente dual la liga española? Análisis gráfico y posibles soluciones

Cuando uno habla con la gente percibe que la liga española de fútbol atrae menos atención que en el pasado, al menos en España. ¿Por qué? Bien sencillo, el FC Barcelona y el Real Madrid tienen tal dominio en ella que las victorias de estos equipos son resultados más que esperados por los espectadores y por tanto uno de los atractivos de un deporte, la incertidumbre en el resultado, disminuye.
Hasta el momento se han disputado 3 jornadas de la Liga BBVA y hay 4 equipos que han ganado los tres partidos que han disputado (Atlético de Madrid, FC Barcelona, Real Madrid y Villarreal). Usando las cuotas de las casas de apuestas deportivas puede calcularse la probabilidad que asignaron las casas de apuestas para cada uno de estos equipos de haber ganado los tres primeros partidos. Usando las cuotas de la casa CODERE APUESTAS la probabilidad que asignaba a ganar estos tres primeros partidos era respectivamente: Atlético de Madrid-11%, FC Barcelona-40%, Real Madrid-47%, Villarreal-7%. Lo cual muestra como las tres victorias por parte del FC Barcelona y Real Madrid eran relativamente esperadas mientras que las tres victorias del Atlético de Madrid (a priori el tercer mejor equipo de la liga BBVA) y el Villarreal eran bastante inesperadas. Pero, ¿siempre ha habido tanta diferencia entre el Real Madrid y el FC Barcelona y el resto de equipos? El siguiente gráfico muestra la probabilidad para todos los equipos de la liga de obtener una determinada puntuación desde la temporada 2007-2008 hasta la temporada 2012-2013.
Funciones de densidad de los puntos al final de la liga BBVA 2007-2013
En este gráfico puede verse como las distribuciones de los dos equipos situados más a la derecha, que se corresponden con el Real Madrid y el FC Barcelona, se van alejando progresivamente del resto de equipos desde la temporada 2007-2008 hasta la temporada 2011-2012. En la temporada 2012-2013 se da un “engañoso” acercamiento de estos equipos al resto que se debe principalmente a la distancia en puntos conseguida por el FC Barcelona sobre el Real Madrid antes de mitad de liga, hecho que provocó que el propio entrenador del Real Madrid dijese en diciembre que la liga estaba prácticamente imposible lo cual provocó que tanto el Real Madrid como el FC Barcelona no pusiesen todo el esfuerzo posible y como consecuencia las probabilidades otorgadas por las casas de apuestas para las victorias de estos equipos fueron más bajas de lo que hubiesen sido en una liga más igualada entre ambos equipos. El motivo de este distanciamiento entre los dos principales clubes y el resto lo explica maravillosamente bien el profesor Gay de Liébana aquíen donde se ve que en los últimos años el FC Barcelona y el Real Madrid han aumentado sus ingresos en una proporción importante mientras que el resto de clubes lo han hecho en una proporción muy reducida.
¿Qué hay que hacer para tener una liga más igualada? La solución adoptada en las ligas profesionales es bien sencilla: que el talento deportivo se distribuya entre los equipos de una forma relativamente equitativa. En ligas cerradas como la NBA se implementan políticas sobre el mercado de jugadores como el draft o límites salariales, pero el sentido de estas políticas desaparece en ligas abiertas en donde los equipos no sólo compiten en la liga nacional pero también en ligas supranacionales como es el caso de la liga BBVA. En este tipo de ligas la solución habitual para tener un mayor balance competitivo es mediante la redistribución de los ingresos de la liga, bien sea a través de los derechos de televisión, los premios por participar, reparto de los ingresos por entradas o por cualquier alternativa que conduzca a un reparto más equitativo de los ingresos de la liga. El problema que tiene para los equipos grandes es que reducir su presupuesto para que aumente el presupuesto de otros equipos significa reducir la probabilidad de ganar la Champions League especialmente a corto plazo que es lo que preocupa a los dirigentes deportivos de estos equipos.
¿Hay alguna alternativa para aumentar la competitividad de la liga sin disminuir las opciones en Champions del FC Barcelona y el Real Madrid? Sí la hay, consiste en usar la misma idea que se utiliza en golf para equilibrar la competición entre distintos golfistas, el hándicap. La siguiente tabla muestra cuántos puntos hubiesen conseguido el Real Madrid y el FC Barcelona bajo tres opciones de hándicap con el resto de equipos así como la puntuación conseguida por el equipo con mayor puntuación que no sea ni el Real Madrid ni el FC Barcelona.
Real Madrid
FC Barcelona
Puntos mejor equipo
Pts.
H. 1
H. 2
H. 3
Pts.
H. 1
H. 2
H. 3
1995-96
70
43
58
47
75
47
59
47
87 (1)
1996-97
92
59
78
61
87
64
75
67
77 (3)
1997-98
63
37
49
36
73
49
61
45
65 (2)
1998-99
68
44
55
37
76
57
70
61
66 (3)
1999-00
62
31
48
39
62
46
55
45
69 (1)
2000-01
80
49
68
61
59
38
53
42
73 (2)
2001-02
66
46
55
40
59
45
56
44
75 (1)
2002-03
78
58
74
62
51
41
46
39
76 (2)
2003-04
70
43
54
41
66
43
58
52
77 (1)
2004-05
80
53
67
53
80
57
72
58
65 (3)
2005-06
70
45
58
48
79
62
70
53
69 (3)
2006-07
76
46
62
45
71
55
62
49
71 (3)
2007-08
85
63
75
54
65
47
57
49
77 (2)
2008-09
78
49
58
45
84
65
82
73
70 (3)
2009-10
96
75
86
67
98
79
90
80
71 (3)
2010-11
92
72
86
73
94
73
82
68
71 (3)
2011-12
100
82
98
90
90
74
88
79
61 (3)
2012-13
85
65
79
67
100
77
92
76
76 (3)
H.1- Hándicap 1- 1 gol en casa y un gol fuera
H.2- Hándicap 2- 1 gol en casa y 0 fuera
H.3- Hándicap 3- 2 goles en casa y 0 fuera
Nota: entre paréntesis el puesto ocupado por el equipo con mayor puntuación sin ser el Real Madrid y FC Barcelona
Lo primero que hay que tener en cuenta que esta son las puntuaciones que hubiesen tenido el Real Madrid y el FC Barcelona aplicando tres tipos de hándicaps ex post. Obviamente si los partidos se hubiesen realizado aplicando ex ante alguno de los hándicaps el Real Madrid y el FC Barcelona se hubiesen comportado de forma distinta dado que con ganar por 1 gol era suficiente mientras que aplicando alguno de los hándicaps podría no serlo. Vemos que desde la temporada 2009-2010, que como se puede ver en el gráfico anterior fue la temporada en la que el Real Madrid y el FC Barcelona se distanciaron del resto de equipos, aplicando el hándicap 1 tanto el Real Madrid como el FC Barcelona hubiesen quedado entre los dos primeros (con excepción del Real Madrid en la temporada 2012-2013) pero con distancia pequeña respecto al tercer equipo. Aplicando el hándicap 2, la distancia seguiría siendo muy alta, mientras que aplicando el hándicap 3 se conseguiría una igualdad mayor.
Por tanto, parece que el uso de hándicaps podría ser una alternativa para tener una liga más igualada y en donde la incertidumbre en los partidos disputados por el Real Madrid y FC Barcelona fuese mucho mayor. Todo ello sin que el Real Madrid o el FC Barcelona tuviesen que tener una peor plantilla que ponga en riesgo la consecución de la Champions.
Este mismo razonamiento debería aplicarlo la liga española de balonmano ASOBAL, en donde tras la desaparición del Atlético de Madrid se da por hecho la victoria en liga del FC Barcelona, y no sólo eso sino que los partidos que quiera ganar fácil lo hará.

Julio del Corral Cuervo. Profesor de Economía en la Universidad de Castilla-La Mancha (síguele en twitter)
Publicado el

Mis impresiones sobre la desaparición del Atlético de Madrid de balonmano

  Historia resumida de una desaparición anunciada– A finales de la década de los 90 Ciudad Real tenía un equipo asentado en la División de Honor del balonmano español, era un equipo modesto, humilde, como corresponde a la capital manchega con una población cercana a los 70.000 habitantes. Sin embargo, uno de los habitantes de Ciudad Real, Domingo  Díaz de Mera (DDM), tenía el sueño de ver al equipo de su tierra vencer por todas las pistas nacionales y europeas de balonmano. Y lo consiguió, a base de invertir una buena cantidad de dinero él así como los gobiernos regionales y locales. Así, se ganaron varias ligas y varias Copas de Europa. La ciudad vibraba con el balonmano, recuerdo en mi primera visita a Ciudad Real allá en el verano del 2005 como los bares no tenían el póster del Real Madrid o Barcelona de fútbol sino que tenían colgados diversos posters del equipo de la ciudad de balonmano. Todo parecía en orden y en un buen estado estacionario, pero en mayo-junio de 2011 con una crisis cada vez más acuciante a lo que se sumaba un cambio en el gobierno regional DDM plantea que el equipo no puede seguir así, que él no está dispuesto a poner tanto dinero y que quiere disolver el equipo, la gran afición al balonmano de Ciudad Real le plantea a  DDM seguir con el equipo en ASOBAL pero con un presupuesto mucho más modesto, a lo que DDM respondió que él no lidera proyectos mediocres…. A raíz de este movimiento en las últimas horas antes de vencer el plazo para la inscripción a ASOBAL DDM consiguió traspasar los derechos federativos del Balonmano Ciudad Real a un club fundado por él con sede en Madrid, el Balonmano Neptuno, nombre que era un claro guiño al que sería su sponsor principal el Atlético de Madrid. De esta manera, un poco “extraña” el Atlético de Madrid vuelve a tener una sección histórica para ese club como el balonmano pero sin ser del Atlético, y desde mi punto de vista este fue uno de los problemas para que no tuviese mucho más tirón. El primer año del balonmano Neptuno fue muy duro para los jugadores en el cual vivían y entrenaban en Ciudad Real pero competían en Madrid, en el cual se enfrentaban continuamente a reproches de aficionados de Ciudad Real (yo coincidí un par de veces en el tren con el equipo y había bastante gente que les recriminaba su marcha, y si hay que tenerlos bien puestos para recriminar algo a 15 tíos de 2 metros y 120 kilos de fuerza pura). El segundo año el bajón de calidad del equipo ya fue notable y para el tercero, que nunca existirá, la bajada de nivel del equipo iba a ser notoria. ¿Cuál era el motivo de esta bajada en la calidad del equipo? Bien sencillo, el presupuesto cada vez menor, los patrocinadores que DDM decía que iba a tener en Madrid pero que no vendrían a Ciudad Real no aparecieron, las instituciones apoyaban pero más de pensamiento que de dinero y los presupuestos se incrementan con euros, no con palabras bonitas en recepciones tras victorias, el público no asistía a los partidos ni regalando entradas. Es decir, se entraba en una espiral muy  peligrosa al que le puso la puntilla Hacienda, sí la misma Hacienda a la que los clubes de fútbol deben más de 600 millones de euros que no quiso negociar una cantidad asumible para un club con el presupuesto del Balonmano Neptuno.

Efectos desaparición ASOBAL
En primer lugar para la liga ASOBAL, la liga de División de honor del balonmano español. En la Economía del Deporte, está más que demostrado que para que una liga tenga interés tiene que tener talento y que además sea competitiva. Pues bien con la desaparición del Atlético de Madrid de balonmano desaparece mucho talento y la liga no va a ser competitiva en el sentido que se puede decir sin miedo a equivocarse quien va a ser el ganador de la liga. Por tanto, los primeros perjudicados van a ser el resto de clubes de ASOBAL, clubes que en la mayoría de los casos están pasando por graves problemas económicos y que van a ver como no van a contar con los ingresos extra que suponía la taquilla de la visita del Atleti. Así mismo, el producto a ofrecer en televisión pierde valor, por tanto menos ingresos para los equipos de liga ASOBAL. Por tanto, la liga ASOBAL va a tener que reinventarse e intentar atraer a espectadores tanto a las canchas como a la televisión. Porque no hay que olvidarse de una cosa, los que deciden el sueldo de unos deportistas no son sus dirigentes, es el aficionado que decide ir a ver los partidos en directo estando dispuesto a pagar una determinada cantidad de dinero, es el aficionado que decide ver en la televisión un determinado partido, es el aficionado el que se compra la camiseta de tal o cual jugador. Si una cosa mostró el Mundial de balonmano en España de enero es que puede haber interés en balonmano.
 Papel Hacienda y políticos
Los equipos de fútbol deben más de 600 millones a Hacienda, y ¿hay algún equipo embargado?? Por ejemplo, el Atlético de Madrid de fútbol tiene una deuda reconocida con Hacienda de más de 100 millones de euros, y el mismo día que se anunció la desaparición del Atlético de Madrid de balonmano fichaba a un jugador con un salario cercano a los 10 millones de euros, ¿tiene Hacienda  el mismo trato con los clubes de fútbol que con otras empresas/sociedades? está claro que no. ¿Tiene Hacienda el mismo trato con los clubes de fútbol que con los clubes de otros deportes? Pues parece ser que tampoco, y si malo es lo primero peor es lo segundo. Señores de Hacienda, HACIENDA SOMOS TODOS, NO? PUES ACTÚEN EN CONSECUENCIA.
Y qué decir de los políticos qué se apuntan a todas las fotos de éxitos deportivos. Pues bien para tener éxitos hay que sembrar y hay que trabajar muy duro para poder entrenar y competir al máximo nivel, y si importante es que el político se apunte a la foto, más importante es que se preocupe por los deportistas y por los clubes mucho antes del éxito. Y mucho más teniendo el condicionante que esta desaparición se produce dos meses antes de la votación de la ciudad que albergará los Juegos Olímpicos.

Para terminar una pregunta capciosa, dado que el apoyo se demuestra apoyando y no respondiendo a preguntas de un cuestionario sin ningún coste, si una ciudad no es capaz de mantener un equipo de primera fila “regalado” en balonmano ¿será capaz de organizar unos Juegos Olímpicos? 
Publicado el

La influencia de las TICs en el precio de las apuestas deportivas

Las apuestas deportivas mueven anualmente miles de millones de euros alrededor del mundo. La importancia de este sector se debe, en gran medida, a la inversión/gasto realizada por los consumidores en apuestas sobre los resultados de los partidos de fútbol. En particular se analiza la evolución del overround, que puede verse como el precio de las apuestas, en las ligas de fútbol en Europa desde la temporada 2000-2001 hasta la actualidad. Antes de su análisis es importante definir el concepto de overround, que se define como la diferencia entre la suma de los inversos de las cuotas de todos los resultados posibles en una apuesta y la unidad. Por ejemplo, durante la temporada 2011-2012, la casa de apuestas británica Bet 365 presentaba las siguientes cuotas para el partido Real Madrid – FC Barcelona:
Ejemplo overround
Cuota
Inverso
Real Madrid
2,40
0,417
Empate
3,50
0,286
Barcelona
2,80
0,357
Suma de inversos
1,060
La suma de los inversos alcanza 1,060, por lo que el valor del overround establecido por Bet 365 para este partido es de 0,060. El valor del overroundserá, obviamente, positivo, ya que de lo contrario surgiría una sure-bet, es decir, una apuesta con ganancia segura para el consumidor.
Desde comienzos de los 2000 la evolución del mercado de apuestas se ha visto influenciada principalmente por dos factores: el incremento de la competencia y el aumento de las posibilidades de arbitraje. Además, la irrupción de Internet en el sector ha contribuido notablemente a aumentar la cantidad de firmas en el mercado y las posibilidades de elección del apostante.
En concreto, analizamos dos hipótesis. En primer lugar se contrasta si el incremento en la competencia en el mercado de las apuestas deportivas, gracias a la introducción de las TICs, ha conllevado, como predice la teoría microeconómica, una disminución en el precio. Y en segundo lugar, se analiza si las casas de apuestas aplican un margen menor en las ligas que atraen a más fans.
Para la elaboración de la base de datos, se ha recurrido a los datos provistos por “http://www.football-data.co.uk/”. Algunas de las observaciones se remontan a la temporada 2000-2001, finalizando con datos de la campaña actual, 2012-2013. En cuanto a las casas de apuestas analizadas, se trata de Interwetten, Bet 365, Gamebookers, William-Hill y Ladbrokes. El siguiente gráfico muestra el overroundpromedio en cada una de las ligas analizadas en la primera temporada disponible (2000-2001) y la última (2012-2013).
Diferencia overround entre temporadas 2000-01 y 2012-13
Mediante el análisis del gráfico se analizan las dos hipótesis analizadas. En primer lugar, vemos como la evolución del overround ha sido decreciente, con valores que han decrecido alrededor de un 50 % en poco más de una década. Antes de la introducción de Internet en el sector, el mercado de apuestas era un sector algo limitado. El número de casas existentes era pequeño, y las posibilidades de apuesta mucho más reducidas. Hoy en día, éste es un sector altamente competitivo. La gran cantidad de competidores existentes en el mismo permite a los consumidores elegir entre múltiples ofertas, con lo que las casas se ven obligadas a reducir sus precios con el objetivo de ser elegidas por los clientes. Los consumidores pueden realizar sus apuestas desde su domicilio, sin necesidad de acudir al establecimiento físico de la compañía como ocurría con anterioridad a la introducción del mercado online. Asimismo, el apostante puede jugar en varias casas, comparando los precios de cada una de ellas y acomodando sus inversiones a la compañía que le ofrezca mejores réditos por las mismas. De esta forma, las casas de apuestas se ven obligadas a reducir sus precios para mantener o aumentar su cuota de mercado.
En cuanto a la segunda hipótesis, de nuevo se comprueba como el valor del overrounden las principales ligas europeas, a las que reunimos en un grupo denominado Top 5 (las primeras divisiones de España, Inglaterra, Alemania, Italia y Francia) es sensiblemente menor al del resto. Ya existían diferencias en la temporada 2000-2001, pero éstas han ido incrementándose con el paso de los años. Esto se debe al objetivo de las casas de apuestas de aumentar su volumen de negocio. Buscan aumentarlo en aquellas ligas que cuentan con un mayor número de clientes potenciales (las cinco principales). Así, la competencia se recrudece. De nuevo, mayor competencia, menor precio.
Para ahondar en este análisis se ha realizado un modelo básico de regresión lineal mediante mínimos cuadrados ordinarios donde la variable dependiente es el overrounden un partido y como variables independientes se incluyen dummies de temporadas, dummies de algunos países, dummies de casa de apuestas y una variable dummy que toma el valor 1 si el partido pertenece a alguna de las cinco principales europeas y esta variable interaccionada con una tendencia temporal.
Estimaciones de un modelo con variable dependiente el overround
Variable
Coeficiente
Variable
Coeficiente
Constante
0,163***
España
–
2000-2001
–
Inglaterra
-0,008***
2001-2002
-0,007***
Alemania
-0,003***
2002-2003
-0,012***
Francia
0,004***
2003-2004
-0,012***
Italia
0,003***
2004-2005
-0,017***
Interwetten
–
2005-2006
-0,020***
Bet 365
-0,037***
2006-2007
-0,022***
Gamebookers
-0,028***
2007-2008
-0,027***
William-Hill
-0,017***
2008-2009
-0,034***
Ladbrokes
-0,011***
2009-2010
-0,041***
No Top 5
–
2010-2011
-0,047***
Top 5
-0,009***
2011-2012
-0,049***
Top 5·t
-0,001***
2012-2013
-0,055***
R2
0,719
Nº observaciones
317.534
*** indica significatividad al 99%
Respecto a los coeficientes estimados, han de interpretarse como la diferencia entre los de las variables omitidas (2000-2001, España, Interwetten y No Top 5) y las incluidas. Se observa como los coeficientes de las variables temporales son decrecientes en el tiempo, lo que indica la evolución descendente seguida por el precio de las apuestas, reduciéndose año tras año. Comparando el valor del overround entre las cinco principales ligas europeas también se constatan pequeñas diferencias, aunque no parecen económicamente significativas. Comparando los precios establecidos por cada una de las casas de apuestas, se comprueba que Interwetten es, con diferencia, la casa que presenta cuotas más caras, muy lejos de los precios establecidos por Bet 365, que se postula como la compañía con precios más competitivos entre las 5 analizadas.  Analizando la diferencia de precios entre las cinco principales ligas europeas (Top 5) y el resto, se observa una diferencia importante. El valor del overround es sensiblemente inferior debido, como se explicó anteriormente, al interés de las casas de apuestas por aumentar el volumen de negocio en estas ligas. Al aumentar la competencia en las mismas, el precio tiende a reducirse. Además, esta diferencia irá creciendo aún más con el paso de los años dado el coeficiente negativo de la variable Top5 interaccionada con la tendencia.
Por tanto, si le gusta apostar y ser racional no lo dude, apueste en alguna de las principales ligas que seguro que el precio de la apuesta será más bajo!!! Y si es averso al riesgo debería apostar en contra de su equipo!!! Así vería el partido con total relajación.
Estudio completo
Sobre los autores:
Jesús Miguel Gómez-Roso Jareño. Recién graduado en ADE en la Universidad de Castilla-La Mancha y se encuentra en busca de trabajo
Julio del Corral Cuervo. Profesor de Economía en la Universidad de Castilla-La Mancha.
Síguele en twitter


Publicado el

Mourinho dejó de ser el special one en la Liga 2012-2013: Eficiencia de los entrenadores en la liga

Muchos premios otorgados a los entrenadores sólo se fijan en la actuación deportiva de los equipos bajo el supuesto que aquellos entrenadores que han conseguido una mejor actuación deportiva como una mejor clasificación en una liga han sido mejores entrenadores. Por ejemplo, en la Liga BBVA el segundo equipo clasificado fue el Real Madrid de Mourinho con lo que se podría argumentar que Mourinho fue el segundo mejor entrenador en la liga por detrás únicamente de Tito Vilanova. Sin embargo, este análisis sólo sería correcto si todos los equipos en una liga dispusiesen del mismo talento deportivo, que como es óbice decir, en la Liga BBVA el talento deportivo no está igualmente repartido entre los equipos. Por este motivo para determinar adecuadamente si la actuación de un entrenador ha sido buena o mala hay que conocer primero los resultados esperados del equipo al que entrena. Para posteriormente comparar la actuación del equipo con lo que se esperaba de él. Si un equipo ha obtenido mejores resultados que los que se esperaban de él, será en gran parte por culpa del entrenador. Al igual que si un equipo no consigue obtener los resultados esperados para él también será mayoritariamente por culpa del entrenador.

Una forma de obtener lo que se espera de un equipo de fútbol es a través de las cuotas de las casas de apuestas deportivas. Las cuotas reflejan el inverso de las probabilidades establecidas por la casa de apuestas ajustadas ligeramente para que la casa tenga un pequeño margen (este suele rondar el 7%). Varios trabajos han obtenido que las probabilidades calculadas a partir de las cuotas de las casas de apuestas son eficientes en el sentido que reflejan bien las probabilidades de los resultados. La probabilidad de obtener una determinada cantidad de puntos para cada equipo puede calcularse a partir de las probabilidades asociadas a las cuotas de los partidos de ese equipo, esto estadísticamente hablando es la función de densidad de los puntos conseguidos por un entrenador. El gráfico a continuación muestra la función de densidad de los puntos del Real Madrid y de la Real Sociedad. Como es de esperar la función de densidad del Real Madrid se sitúa mucho más a la derecha que la función de densidad de la Real Sociedad.
Una vez calculada estas funciones se puede calcular la probabilidad de que el número de puntos obtenido por un equipo sea igual o menor que un determinado número de puntos. Para ello lo único que hay que hacer es sumar la probabilidad de haber obtenido desde cero puntos hasta una determinada cantidad de puntos, esto se conoce como función de distribución. La siguiente figura muestra las funciones de distribución de los puntos de Mourinho y Montanier.
El valor de la función de distribución en el número de puntos conseguido por un entrenador puede verse como una medida de la eficiencia del entrenador, en el sentido que es la probabilidad de que un equipo entrenado por un entrenador hubiera obtenido menos o los mismos puntos que realmente obtuvo. Como es una probabilidad el valor se sitúa entre 0 y 1, cuánto más próximo esté este valor a 1 mejor habrá sido la actuación del entrenador. En los gráficos la línea vertical muestra los puntos conseguidos por cada uno de los equipos. Así la eficiencia de un entrenador es la probabilidad a la que se cruzan la línea vertical y la función de distribución que como puede verse está cerca de 0.5 para Mourinho y próximo a 1 para Montanier. 
La siguiente tabla muestra la eficiencia de cada uno de los entrenadores en la Liga BBVA en la temporada 2012/2013. Como puede verse los tres entrenadores más eficientes fueron Montanier, Tito Vilanova y Javier Aguirre por este orden. Mientras que los tres entrenadores más ineficientes fueron Oltra, Paco Herrera y Pochettino. Todos ellos fueron despedidos por sus respectivos equipos. El único entrenador de los 8 más ineficientes que no fue despedido fue Manolo Jiménez del Real Zaragoza. Por su parte Mourinho,  obtiene un valor de 0.50, lo que le convierte en un entrenador mediano, por lo que parece que en la Liga BBVA de la temporada 2012-2013 el Special one no fue tan bueno. 
Eficiencia de los entrenadores en la Liga BBVA 2012/2013
Entrenador
Equipo
Puntos
Partidos
Eficiencia
Montanier
Real Sociedad
66
38
0.977
Tito Vilanova
F.C. Barcelona
100
38
0.958
Javier Aguirre
R.C.D. Español
35
25
0.909
Paco Jémez
Rayo Vallecano
53
38
0.908
Simeone
Atlético de Madrid
76
38
0.907
Valverde
Valencia C.F.
47
24
0.905
Pepe Mel
Real Betis Balompié
56
38
0.877
Manzano
R.C.D. Mallorca
19
16
0.833
Lucas Alcaraz
Granada C.F.
22
17
0.789
Juan Ignacio Martínez
Levante U.D.
46
38
0.726
Pellegrini
Málaga C.F.
57
38
0.687
Luis García
Getafe C.F.
47
38
0.671
Fernando Vázquez
Deportivo de La Coruña
19
15
0.640
Djukic
Real Valladolid
43
38
0.540
Abel Resino
Celta de Vigo
17
14
0.503
Mourinho
Real Madrid
85
38
0.502
Emery
Sevilla C.F.
28
19
0.396
Anquela
Granada C.F.
20
21
0.394
Bielsa
Athletic de Bilbao
45
38
0.298
Mendilibar
C.A. Osasuna
39
38
0.266
Pellegrino
Valencia C.F.
18
14
0.225
Domingo Paciencia
Deportivo de La Coruña
4
6
0.213
Michel
Sevilla C.F.
22
19
0.163
Jiménez
Real Zaragoza
34
38
0.107
Caparrós
R.C.D. Mallorca
17
22
0.094
José Luis Oltra
Deportivo de La Coruña
12
17
0.084
Paco Herrera
Celta de Vigo
20
24
0.079
Pochettino
R.C.D. Español
9
13
0.048
Notas: elaborada usando las cuotas de CODERE APUESTAS
Los entrenadores están ordenados en orden decreciente de la eficiencia.
En cursiva aquellos entrenadores que fueron despedidos.
Una de las muchas críticas que se puede hacer a esta metodología, es que las cuotas también llevan implícitas la calidad del entrenador. Es cierto, puede ser verdad, pero mi teoría es que la calidad del entrenador afecta muy poco a lo que se espera de los resultados de un equipo mientras que lo que sí importa es la calidad de los jugadores. En otras palabras, los jugadores son los que definen la frontera, las posibilidades de producción de un equipo y la capacidad/habilidad del entrenador es lo que delimita lo cerca o lo lejos que se sitúe un equipo de su frontera de posibilidades. Como ejemplo, el siguiente gráfico muestra las funciones de densidad del FC Barcelona en la temporada 2011-2012 con Guardiola al frente y en la temporada 2012-2013 con Tito al frente. Puede verse como las funciones de densidad son relativamente similares. Dos hechos pueden explicar este hecho: el cambio de entrenador y que en la temporada 2012-2013 la liga estuvo virtualmente decidida durante muchas jornadas lo que como consecuencia tenía, al menos a priori, una no victoria blaugrana más probable.
Para ver que hipótesis de las dos es más plausible se muestra el gráfico con las funciones de densidad sólo en la primera vuelta de la liga. Se ve claramente como las funciones de densidad del FC Barcelona en la primera vuelta son bastante similares incluso con cambio de entrenador, con lo que parece que la diferencia en las funciones de densidad anuales se deben a una menor trascendencia de las victorias en la temporada 2012-2013 que al cambio de entrenador.
Publicado el

Managers’ Efficiency in the English Premier League in the season 2012-2013

Odds for football matches offered in the betting market can be reconverted into probabilities for each possible result (home win, draw, away win). If the betting market were efficient, these probabilities would reflect the true probabilities of each event. Although there is no consensus in the literature whether or not betting odds are efficient, it seems that any inefficiency that arises is very small. Thus, the probabilities embedded in betting odds can be seen as true probabilities. The European domestic football leagues are generally organized in a double round robin basis, where each team plays against the other teams once at home and once away. Winning teams are awarded three points, a draw earns one point for each team, and the losing team earns no points. The final league ranking is made on the basis of points earned at the end of the double round robin.
Basic probability theory tells us that the joint probability of two independent events (e.g., a victory of the same team in two different football matches) equals the product of their probabilities.Using this simple formula for all possible combinations of match results of each team, the probability of each team within a league obtaining a certain amount of points can be computed, that is, the density function of total points at the end of the season. The total points ranges between zero (i.e., the team loses all matches) and the product of the number of matches and three (i.e., the team wins all matches).
In particular, we use the betting odds from CODERE APUESTAS in order to calculate the density functions for the 2012-13 season for English Premier League. The cumulative density function can be used to calculate the probability of getting more points than the actual result. The inverse of that probability can be viewed as an efficiency index for managers in the sense than the closer the value to one will reflect a better performance and the closer the value to zero will reflect a worse performance. The managers with higher efficiencies would be the teams that have overperformed the results expected from the odds. The overperforming could be due to luck or fortunate referees’ decisions, but the most plausible reason to overperform the expected results from the odds is good coaching, in the same way the underperformance of the teams could be due to injuries or bad luck but the most plausible is bad coaching. Thus, the efficiency index can be understood as a measure of the performance of the managers.
Table 1 shows the managers’ efficiency in the season 2012/2013. It can be seen that Sir Alex Ferguson in his last season was the best manager followed by André Villas-Boas from the Tottenham Hotpsur. On the other hand the worst managers have been Mark Hughes and Harry Redknapp. It is noteworthy to indicate that the weighted average of the efficiency was 0.52, so all managers with a efficiency over 0.52 have been more efficient than the average.
Table 1. Efficiencies of the managers in the season 2012/2013
Manager
Team
Points
Matches
Efficiency
Alex Ferguson
Manchester United
89
38
0.96
André Villas-Boas
Tottenham Hotpsur
72
38
0.90
Chris Hughton
Norwich City
44
38
0.74
Arsène Wenger
Arsenal
73
38
0.71
Steve Clarke
West Bromwich Albion
49
38
0.70
Roberto Di Matteo
Chelsea
24
12
0.69
Paolo Di Canio
Sunderland
8
7
0.68
Rafa Benítez
Chelsea
51
26
0.66
Roberto Mancini
Manchester City
75
36
0.66
David Moyes
Everton
63
38
0.65
Sam Allardyce
West Ham United
46
38
0.63
Paul Lambert
Aston Villa
41
38
0.57
Michael Laudrup
Swansea City
46
38
0.55
Mauricio Pochettino
Southampton
19
16
0.50
Nigel Adkins
Southampton
22
22
0.46
Tony Pulis
Stoke City
42
38
0.40
Nigel Adkins
Reading
5
8
0.37
Martin Jol
Fulham
43
38
0.35
Martin O’Neill
Sunderland
31
31
0.33
Brian Kidd
Manchester City
3
2
0.29
Brendan Rogers
Liverpool
61
38
0.24
Brian McDermott
Reading
23
29
0.21
Roberto Martínez
Wigan Athletic
36
38
0.21
Alan Pardew
Newcastle United
41
38
0.21
Harry Redknapp
Queens Park Rangers
21
26
0.16
Mark Hughes
Queens Park Rangers
4
12
0.03
Eamonn Dolan
Reading
0
1
0.00
Notes: elaborated using the betting odds from CODERE APUESTAS
Managers are ordered by the efficiency level.
In italics managers that were fired
Julio del Corral Cuervo is Associate professor in Economics at the University of Castilla-La Mancha (Spain)
* These results will be presented at the Fourth Spanish Conference in Sports Economics (Madrid, June 2013).
Publicado el

Balance competitivo en el fútbol europeo en la temporada 2011-2012: La liga española fue más escocesa que la liga escocesa

El análisis del balance competitivo en la Economía del Deporte comenzó cuando Simon Rottenberg escribió en 1956 “Es necesario que la distribución del talento sea más o menos equitativa para que exista incertidumbre sobre el resultado y la existencia de incertidumbre en el resultado es necesaria para que los consumidores estén dispuestos a pagar por ver un partido”. Desde entonces muchos autores han analizado la relación entre la igualdad de los competidores con el espectáculo que se genera. Aunque la evidencia empírica no ha resultado siempre favorable a la hipótesis de Rottenberg si se ha corroborado dicha hipótesis en muchos trabajos.
La mayoría de las medidas del balance competitivo usadas en la literatura usan los resultados en la liga para calcular diferentes medidas de desigualdad en los puntos conseguidos por los equipos (desviación típica de los puntos, ratio entre puntos conseguidos por los 4 primeros clasificados y los 4 últimos clasificados). Es decir, son medidas ex posten el sentido que valoran los resultados pero no valoran la percepción de los aficionados de si los partidos ex antevan a ser partidos disputados. Obviamente la percepción de que el partido va a ser disputado es el dato relevante para los aficionados a la hora de tomar la decisión de asistir al partido o no asistir, dado que lo importante no es que el partido resulte disputado sino que los aficionados prevean que el partido va a ser disputado.  
Las casas de apuestas deportivas establecen cuotas para los diferentes resultados de un partido. Las cuotas reflejan el inverso de las probabilidades establecidas por la casa de apuestas ajustadas ligeramente para que la casa tenga un pequeño margen (este suele rondar el 10%). Una vez conocida la probabilidad de cada resultado para todos los equipos  en todos los partidos de una liga es posible determinar cuál es la probabilidad de cada equipo de obtener un determinado número de puntos. Lo único que se necesita conocer es que la probabilidad de dos sucesos independientes es el producto de las probabilidades de cada uno de ellos. Por ejemplo si la probabilidad de que el Real Madrid gane al Sporting de Gijón es del 90% y la probabilidad de que el Real Madrid gane al Barcelona es del 40%, la probabilidad de que el Real Madrid gane esos dos encuentros es del 36% (0,9 x 0,4=0,36). [1]
Replicando esto para todos los partidos se puede construir lo que se conoce como una distribución de la probabilidad del número de puntos para cada equipo. Así, si un equipo tiene probabilidades altas de victoria en todos sus partidos, la probabilidad de obtener una gran cantidad de los puntos en disputa al final de la liga (por ej., 90 puntos si en la liga se disputan 38 partidos) será “relativamente” alta, mientras que la probabilidad de obtener pocos puntos al final de la liga (por ej., 40 puntos) será baja, esto lo que ocurre a los mejores equipos de la liga como El Real Madrid, F.C. Barcelona o Bayern Munich. Por el contrario, los equipos que tienen probabilidades bajas de victoria en la mayoría de partidos de la liga, tendrán una probabilidad muy baja de obtener una gran cantidad de puntos y una probabilidad más alta de obtener 40 puntos.
El siguiente gráfico muestra la distribución de la probabilidad del número de puntos para cada equipo en las 5 principales ligas europeas en la temporada 2011-2012: Liga BBVA (España), Bundesliga (Alemania), Serie A (Italia), Premier League (Inglaterra) y Ligue 1 (Francia). Adicionalmente se incorpora la Scottish Premier League por ser el ejemplo típico de una liga desigual con dos equipos con una diferencia de calidad notoria respecto al resto.
En el gráfico se observa claramente como la liga española es la más desigual, donde hay dos equipos (Real Madrid y F.C. Barcelona), muy por encima del resto. Esta tendencia es similar en la liga escocesa pero de forma más atenuada La liga donde existía un mayor balance competitivo era la francesa seguida de la italiana. En la liga inglesa hay dos grupos relativamente diferenciados. En uno primero estarían Manchester United, Manchester City, Chelsea, Arsenal, Liverpool y Tottenham y en el otro el resto.
En la siguiente tabla se muestra las probabilidades de cada uno de los equipos de la liga española de haber conseguido como máximo los puntos con los que descendió el equipo con mejor puntuación que descendió (Villarreal), y como mínimo los puntos que dieron acceso a la Europa League (Levante), a la Champions League (Málaga), a la Champions League de forma directa (F.C. Barcelona) y a ganar la liga (Real Madrid).[1]
Equipo
Descenso
UEFA
Champions
Champions directa
Liga
Athletic Bilbao
4,440%
47,932%
32,590%
0,000%
0,000%
Atlético de Madrid
0,611%
77,843%
64,425%
0,002%
0,000%
F.C. Barcelona
0,000%
100,000%
100,000%
67,692%
14,764%
Real Betis
19,794%
18,734%
9,992%
0,000%
0,000%
R.C.D. Español
21,449%
16,960%
8,814%
0,000%
0,000%
Getafe C.F.
28,540%
11,900%
5,747%
0,000%
0,000%
Granada C.F.
61,695%
2,016%
0,720%
0,000%
0,000%
Levante U.D.
34,124%
9,011%
4,121%
0,000%
0,000%
Málaga C.F.
1,688%
64,548%
48,964%
0,000%
0,000%
R.C.D. Mallorca
34,008%
9,172%
4,224%
0,000%
0,000%
C.A. Osasuna
28,265%
12,126%
5,888%
0,000%
0,000%
Real Madrid
0,000%
100,000%
100,000%
46,532%
5,574%
Racing de Santander
69,965%
1,130%
0,371%
0,000%
0,000%
Sevilla F.C.
1,912%
62,996%
47,413%
0,000%
0,000%
Real Sociedad
41,095%
6,314%
2,701%
0,000%
0,000%
Sporting de Gijón
58,824%
2,428%
0,893%
0,000%
0,000%
Valencia C.F.
0,344%
83,045%
71,120%
0,004%
0,000%
Rayo Vallecano
36,838%
8,188%
3,718%
0,000%
0,000%
Villarreal C.F.
11,633%
29,265%
17,335%
0,000%
0,000%
Real Zaragoza
52,614%
3,357%
1,287%
0,000%
0,000%
Nota: elaboración propia con datos provenientes de CODERE. Los datos están redondeados al tercer decima.
La cifra más representativa que muestra la desigualdad en la liga entre los dos primeros equipos y el resto, es la probabilidad de haber conseguido al menos los puntos que dieron acceso a la Champions directa. Esta probabilidad fue del 0,004% para  el Valencia y un 0,002% en el caso del Atlético de Madrid, mientras que para el resto de equipos fue menor que el 0,001%. También es llamativa que la probabilidad del Real Madrid y el F.C. Barcelona de conseguir al menos los puntos necesarios para clasificarse para Champions es del 100%.
Visto esto y después de hablar con muchos aficionados está claro que la Liga BBVA está perdiendo mucho atractivo, y si bien juegan en ella dos de los mejores equipos del mundo el resto de equipos son cada vez más flojos y lo que es peor con una tendencia decreciente. Como muestra el Málaga y el Valencia tuvieron que vender el verano pasado  a varios de sus mejores jugadores y son dos de los equipos que podrían optar a estar cerca de los dos grandes. El 27 de Abril habrá elecciones en la Liga de Fútbol Profesional, así que por el bien del fútbol español esperemos que el nuevo presidente sea capaz de reconducir esta situación.
Julio del Corral Cuervo es profesor contratado doctor en Economía en la Universidad de Castilla-La Mancha.
* Agradezco la ayuda en el tratamiento de la información de Jesús Gómez-Roso, así como los comentarios recibidos de Fernando del Corral.
** Una versión de este trabajo se ha enviado para su posible publicación a una revista científica, la versión completa puede descargarse en este enlace:


[1]Bueno y un poquito de programación dado que hacer esto a mano es totalmente inviable.
Publicado el

A comparison between efficiency from traditional techniques and those derived from odds

The traditional methodology to calculate the efficiency of decision making units is to estimate a frontier either using non-parametric techniques (e.g., DEA) or parametric techniques (e.g., stochastic frontier models). In order to do this the output and inputs need to be established. If the purpose is to calculate the efficiency of teams/managers in a sport league there is a consensus to use the number of points or winnings as output and quality measures of the squad as inputs. Once it is estimated the frontier to calculate the efficiency index is straightforward by diving observed output by the frontier output given the inputs.
I have recently proposed (http://footballperspectives.org/ranking-football-managers-big-5-leagues-2011-12-season) an alternative way to calculate the efficiency of managers by using odds. The idea is quite simple, first it has to be computed the probability for the teams of getting a certain amount of points at the end of the league given the odds[1], that means that it is calculated the density function of the points at the end of the league. Thereafter, it can be computed the probability of the cumulative distribution function at the actual number of points. In other words, it is computed the probability that a certain team would have done less points. This figure can be interpreted as an efficiency index given that it is bounded between zero and one and that the greater the value the greater the efficiency.
Next, I am going to compare the efficiencies that arises from estimating a production frontier for the coaches in the Liga BBVA at the season 2011-2012 (http://footballperspectives.org/efficiency-managers-spanish-football-league-2011-12-season) and the efficiency of the teams derived from the odds. To estimate the production function it was used as output the ratio between points obtained and the total possible points (i.e., 3 x the number of matches) and as input the value of the most valuable goalkeeper, 6 defenders, 6 defenders, and 3 forwards from http://www.transfermarkt.co.uk.
Table 1 shows such comparison.
Team
Squad €
Points
TE frontier
Rank frontier
TE odds
Rank odds
Rank diff.
Levante U.D.
2.6E+07
55
100.0%
1
93.0%
2
1
Real Madrid C.F.
4.6E+08
100
100.0%
2
96.2%
1
-1
C.A. Osasuna
3.0E+07
54
95.0%
3
87.9%
3
0
F.C. Barcelona
5.5E+08
91
88.0%
4
38.2%
14
10
R.C.D. Mallorca
4.4E+07
51
83.0%
5
85.7%
4
-1
Real Betis Balonpié
3.4E+07
47
81.0%
6
48.4%
11
5
Rayo Vallecano
2.2E+07
43
81.0%
7
47.4%
12
5
Valencia C.F.
1.3E+08
61
80.0%
8
49.0%
10
2
Málaga C.F.
1.0E+08
58
79.0%
9
56.3%
9
0
Getafe C.F.
5.2E+07
47
74.0%
10
59.8%
8
-2
R.C.D. Espanyol
4.7E+07
46
74.0%
11
45.5%
13
2
Real Sociedad
6.0E+07
47
72.0%
12
72.3%
5
-7
Atlético de Madrid
1.5E+08
56
70.9%
13
30.8%
16
3
Real Zaragoza
4.4E+07
43
70.3%
14
63.4%
7
-7
Granada C.F.
4.3E+07
42
68.5%
15
66.8%
6
-9
Athletic de Bilbao
1.1E+08
49
67.0%
16
26.9%
17
1
Sevilla F.C.
1.2E+08
50
66.0%
17
19.4%
18
1
Sporting de Gijón
3.9E+07
36
59.9%
18
37.0%
15
-3
Villarreal C.F.
1.5E+08
41
51.9%
19
11.6%
19
0
Racing de Santander
2.8E+07
27
48.4%
20
6.8%
20
0
Mean
75.5%
52.1%
SD
0.14
0.26
Corr TE frontier-squad
0.34
Corr TE odds-squad
0.02
There is one team that is really benefited from obtained the efficiency using the production instead by using the odds methodology, FC Barcelona. Why? To answer this question is worthy to analyze the following picture that helps to explain how it works the production function methodology.

[1] In doing so the odds are converted into probabilities and subsequently it is used the formula that tells us that the joint probability of two independent events (e.g., a victory of the same team in two different football matches) equals the product of their probabilities. Using this simple formula for all possible combinations of match results of each team, the probability of each team within a league obtaining a certain amount of points can be computed. The total points ranges between zero (i.e., the team loses all matches) and the product of the number of matches and three (i.e., the team wins all matches). In particular, we use the betting odds from CODERE APUESTAS.
Publicado el

A comparison between efficiency from traditional techniques and those derived from odds

The traditional methodology to calculate the efficiency of decision making units is to estimate a frontier either using non-parametric techniques (e.g., DEA) or parametric techniques (e.g., stochastic frontier models). In order to do this the output and inputs need to be established. If the purpose is to calculate the efficiency of teams/managers in a sport league there is a consensus to use the number of points or winnings as output and quality measures of the squad as inputs. Once it is estimated the frontier to calculate the efficiency index is straightforward by diving observed output by the frontier output given the inputs.
I have recently proposed (http://footballperspectives.org/ranking-football-managers-big-5-leagues-2011-12-season) an alternative way to calculate the efficiency of managers by using odds. The idea is quite simple, first it has to be computed the probability for the teams of getting a certain amount of points at the end of the league given the odds[1], that means that it is calculated the density function of the points at the end of the league. Thereafter, it can be computed the probability of the cumulative distribution function at the actual number of points. In other words, it is computed the probability that a certain team would have done less points. This figure can be interpreted as an efficiency index given that it is bounded between zero and one and that the greater the value the greater the efficiency.
Next, I am going to compare the efficiencies that arises from estimating a production frontier for the coaches in the Liga BBVA at the season 2011-2012 (http://footballperspectives.org/efficiency-managers-spanish-football-league-2011-12-season) and the efficiency of the teams derived from the odds. To estimate the production function it was used as output the ratio between points obtained and the total possible points (i.e., 3 x the number of matches) and as input the value of the most valuable goalkeeper, 6 defenders, 6 defenders, and 3 forwards from http://www.transfermarkt.co.uk.
Table 1 shows such comparison.
Team
Squad €
Points
TE frontier
Rank frontier
TE odds
Rank odds
Rank diff.
Levante U.D.
2.6E+07
55
100.0%
1
93.0%
2
1
Real Madrid C.F.
4.6E+08
100
100.0%
2
96.2%
1
-1
C.A. Osasuna
3.0E+07
54
95.0%
3
87.9%
3
0
F.C. Barcelona
5.5E+08
91
88.0%
4
38.2%
14
10
R.C.D. Mallorca
4.4E+07
51
83.0%
5
85.7%
4
-1
Real Betis Balonpié
3.4E+07
47
81.0%
6
48.4%
11
5
Rayo Vallecano
2.2E+07
43
81.0%
7
47.4%
12
5
Valencia C.F.
1.3E+08
61
80.0%
8
49.0%
10
2
Málaga C.F.
1.0E+08
58
79.0%
9
56.3%
9
0
Getafe C.F.
5.2E+07
47
74.0%
10
59.8%
8
-2
R.C.D. Espanyol
4.7E+07
46
74.0%
11
45.5%
13
2
Real Sociedad
6.0E+07
47
72.0%
12
72.3%
5
-7
Atlético de Madrid
1.5E+08
56
70.9%
13
30.8%
16
3
Real Zaragoza
4.4E+07
43
70.3%
14
63.4%
7
-7
Granada C.F.
4.3E+07
42
68.5%
15
66.8%
6
-9
Athletic de Bilbao
1.1E+08
49
67.0%
16
26.9%
17
1
Sevilla F.C.
1.2E+08
50
66.0%
17
19.4%
18
1
Sporting de Gijón
3.9E+07
36
59.9%
18
37.0%
15
-3
Villarreal C.F.
1.5E+08
41
51.9%
19
11.6%
19
0
Racing de Santander
2.8E+07
27
48.4%
20
6.8%
20
0
Mean
75.5%
52.1%
SD
0.14
0.26
Corr TE frontier-squad
0.34
Corr TE odds-squad
0.02
There is one team that is really benefited from obtained the efficiency using the production instead by using the odds methodology, FC Barcelona. Why? To answer this question is worthy to analyze the following picture that helps to explain how it works the production function methodology.

                                         Note: The red line indicates the estimated production function
FC Barcelona with a bit better squad than Real Madrid earned 93 points instead of 100 of Real Madrid. Real Madrid is on the frontier, thus the efficiency index of FC Barcelona is calculated dividing 93 by a figure a bit greater than 100. The result is that the efficiency from the production function was 0.88. The interpretation is that to be fully efficient FC Barcelona would have to gain 106 points. 0.88 is a high efficiency index, the fourth in the ranking, but the league from FC Barcelona was so good?
According to the odds in order to make a season on the average (0.52) FC Barcelona would had to gain 95 points (the red line) but it did 91 points (the green line). Now let us assume that FC Barcelona would have gained 80 points, ceteris paribus. In the production frontier the efficiency would be close to 0.8, so a high efficiency but in the odds methodology the efficiency would be around 0.05, so a very bad season that is a much more sensible efficiency index.
On the other hand, Real Sociedad, Real Zaragoza and Granada were considered quite inefficient in the production function approach (i.e., 12, 14 and 15 respectively in the rank) but they were considered quite efficient in the odds approach (i.e., 5, 7, 6 respectively in the rank). Why do arise these huge differences? The answer is the over-performing of Levante. Levante with a close squad quality to these teams performed a really good season, thus the frontier for these teams is defined by the Levante. Thus, even though they have done a really good season according to the expectations from the odds they were not considered such good in the production function. So, once again the odds methodology seems to be appropriate than the production function in this framework since the efficiency of a team does not depend from a over-performing of other team.
Last but no least the coefficient of correlation between the efficiency from the production function and the squad value was 0.34 whereas the coefficient of correlation between the efficiency from odds and the squad value was 0.02. That is, the production frontier methodology is not able to produce an efficiency index not related with the quality of the teams but the efficiencies using the odds methodology are not related at all with the quality of teams which is an adequate property for the efficiencies.
Thus, the efficiencies of managers/clubs derived from the odds look to be a good alternative to the well-established production function approach.
* I acknowledge the valuable assistance in recording the data from Fernando del Corral, Raúl Laguna and Jesús Gómez-Roso.

[1] In doing so the odds are converted into probabilities and subsequently it is used the formula that tells us that the joint probability of two independent events (e.g., a victory of the same team in two different football matches) equals the product of their probabilities. Using this simple formula for all possible combinations of match results of each team, the probability of each team within a league obtaining a certain amount of points can be computed. The total points ranges between zero (i.e., the team loses all matches) and the product of the number of matches and three (i.e., the team wins all matches). In particular, we use the betting odds from CODERE APUESTAS.
Publicado el

Ni Mourinho, ni Guardiola. El mejor entrenador de las principales ligas europeas en la temporada 2011-2012 fue… René Girard (Montpellier)

Jose Mourinho con sus declaraciones recientes a la RTP sobre una posible corrupción en el premio al mejor entrenador del año de la FIFA ha re-abierto el interés por conocer quién fue el mejor entrenador en la temporada 2011-2012. Una forma de elaborar un ranking de los entrenadores consiste en utilizar técnicas frontera (e.g., frontera estocástica o Data Envelopment Analysis) donde es necesario disponer de una medida de la calidad de la plantilla y una medida de los resultados obtenidos para obtener la eficiencia de los entrenadores. El problema del uso de estas técnicas es que no permiten comparar a entrenadores de diferentes ligas, dado que se estarían comparando en cierto sentido naranjas con limones. Una alternativa a las tradicionales técnicas frontera para calcular la eficiencia de los entrenadores es calcular cual es la probabilidad de haber realizado una temporada con peores resultados, para ello es necesario conocer cuáles son los resultados esperados de un equipo. La ventaja de usar esta metodología es que si se puede comparar la eficiencia de equipos en distintas ligas, permitiendo decir quién fue el mejor entrenador en una temporada.
Una forma de obtener lo que se espera de un equipo de fútbol es a través de las cuotas de las casas de apuestas. Las cuotas reflejan el inverso de las probabilidades establecidas por la casa de apuestas ajustadas ligeramente para que la casa tenga un pequeño margen (este suele rondar el 10%). Varios trabajos han obtenido que las probabilidades calculadas a partir de las cuotas de las casas de apuestas son eficientes en el sentido que reflejan bien las probabilidades de los resultados.
Para calcular el nivel de eficiencia de los equipos (entrenadores si ha sido el mismo durante toda la temporada) en esa liga se necesita conocer la probabilidad de cada resultado para todos los equipos en todos los partidos de una liga para determinar cuál es la probabilidad de cada equipo de obtener un determinado número de puntos. Lo único que se necesita conocer es que la probabilidad de dos sucesos independientes es el producto de las probabilidades de cada uno de ellos. Por ejemplo si la probabilidad de que el Real Madrid gane al Sporting de Gijón es del 90% y la probabilidad de que el Real Madrid gane al Barcelona es del 40%, la probabilidad de que el Real Madrid gane esos dos encuentros es del 36% (0,9 x 0,4=0,36).[1]Replicando este cálculo para todos los partidos de una liga se puede calcular cuál es la probabilidad de haber obtenido cada una de las puntuaciones posibles en la liga de cada equipo, esto es lo que se conoce en estadística como función de densidad de los puntos de la liga. El mínimo de puntos son 0 puntos, si se pierden todos los partidos, y el máximo es el producto del número de partidos y 3 puntos, que por ejemplo para el caso español es de 114. A continuación se muestra la función de densidad para el Real Madrid.

Como puede verse, la probabilidad alcanza su valor máximo alrededor de 90 puntos, mientras que la probabilidad desciende a medida que nos movemos bien a la derecha o a la izquierda. Una vez construida la función de densidad puede calcularse que proporción de la función de densidad queda a la izquierda de los puntos realmente obtenidos (en el caso del Real Madrid, 100 puntos). Para ello simplemente hay que sumar la probabilidad de todas las posibles puntuaciones desde cero puntos hasta la puntuación realmente obtenida. Por ejemplo, en el caso del Real Madrid este valor es 0,962. Lo que implica que la probabilidad de haber obtenido más puntos de los que realmente obtuvo fue de 0,038 o 3,8% en términos porcentuales. Esto refleja que la liga del Real Madrid fue bastante buena. El valor de 0,962 ó 96,2% en términos porcentuales puede verse como una medida de la eficiencia (Ef.) del equipo en la competición liguera dado que indica la relación que existe en términos de probabilidad entre los resultados obtenidos por el equipo y los resultados previstos para el equipo. Cuanto este valor este más próximo a 1 mejor habrá sido la temporada del equipo teniendo en cuenta su potencial, mientras que cuánto más próximo esté a cero peor habrá sido la temporada respecto a su potencial.
La tabla que está en la siguiente página tiene ordenados de mayor a menor a los equipos de las principales ligas europeas (Liga BBVA, Serie A, Bundesliga, Premier League y Ligue 1) en función del valor de la eficiencia. En primer lugar está el Montpellier H.S.C., equipó que contra todo pronóstico resultó vencedor de la Ligue 1. El primer equipo español que aparece en la tabla es el Real Madrid, que ocupa el cuarto puesto, mientras que el Levante ocupa el noveno puesto con un valor de la eficiencia del 93%. Otros equipos grandes a nivel europeo que hicieron una buena temporada fueron el Borussia Dortmund (98,1%), Manchester City (94,9%), Manchester United (92,4%), Juventus de Turín (91,5%) y el Paris Saint Germain (90,9%). Por el contrario equipos grandes europeos que tuvieron una mala actuación en su liga fueron el Liverpool (2,6%), el Chelsea (12%) y el Inter de Milán (17,8%). A nivel español los equipos con un nivel más bajo de eficiencia fueron el Racing de Santander (6,8%), Villarreal (11,6%) y el Sevilla (19,4%).
Por tanto, si sólo se tuviesen en cuenta los resultados en las principales ligas europeas de fútbol en la temporada 2011-2012 el mejor entrenador sería René Girard que fue el entrenador del Montpellier. Mourinho por su parte quedaría en una más que meritoria cuarta plaza.

Ranking
Equipo
Ef.
País
Ranking
Equipo
Ef.
País
Ranking
Equipo
Ef.
País
1
Montpellier H.S.C.
99,8%
F
34
Toulouse F.C.
69,5%
F
67
 1899 Hoffenheim
33,4%
A
2
Newcastle U.F.C.
98,3%
ING
35
A.C. Ajaccio
68,7%
F
68
U.S. Lecce
30,8%
ITA
3
B.V. Borussia 09 D.
98,1%
A
36
Stade Rennais F.C.
67,4%
F
69
Atlético de Madrid
30,8%
E
4
Real Madrid
96,2%
E
37
Granada C.F.
66,8%
E
70
Dijon Football Côte d’Or
30,0%
F
5
 Borussia M’gladbach
95,6%
A
38
Tottenham Hotspur F.C.
65,5%
ING
71
Novara Calcio
29,3%
ITA
6
Manchester City F.C.
94,9%
ING
39
Everton F.C.
65,2%
ING
72
Bolton Wanderers F.C.
28,5%
ING
7
 F.C. Schalke 04
93,2%
A
40
Real Zaragoza
63,4%
E
73
Valenciennes F.C.
28,3%
F
8
Levante U.D.
93,0%
E
41
Calcio Catania
60,7%
ITA
74
 F.S.V. Mainz 05
27,8%
A
9
Manchester United
92,4%
ING
42
Getafe C.F.
59,8%
E
75
A.S. Roma
27,6%
ITA
10
Juventus de Turín
91,5%
ITA
43
AS Nancy-Lorraine
58,5%
F
76
U.S. Città di Palermo
27,6%
ITA
11
Paris Saint Germain
90,9%
F
44
 F.C. Nürnberg
57,6%
A
77
Athletic de Bilbao
26,9%
E
12
 Bologna F.C. 1909
90,7%
ITA
45
Arsenal F.C.
57,5%
ING
78
F.C. Köln
26,7%
A
13
Parma F.C.
90,4%
ITA
46
 V.f.L. Wolfsburg
56,9%
A
79
Stade Malherbe Caen
21,0%
F
14
C.A. Osasuna
87,9%
E
47
Malaga C.F.
56,3%
E
80
A.C.F. Fiorentina
19,7%
ITA
15
R.C.D. Mallorca
85,7%
E
48
 Bayer 04 Leverkusen
54,6%
A
81
Sevilla F.C.
19,4%
E
16
Norwich City F.C.
84,5%
ING
49
 Atalanta B.C.  
52,8%
ITA
82
Genoa C.F.C.
18,3%
ITA
17
Wigan Athletic
81,9%
ING
50
Stoke City F.C.
49,7%
ING
83
F.C. Internazionale Milano
17,8%
ITA
18
 Évian Thonon Gaillard F.C.
81,8%
F
51
Valencia C.F.
49,0%
E
84
 S.V. Werder Bremen
17,7%
A
19
LOSC Lille Métropole
81,1%
F
52
Sunderland A.F.C.
48,7%
ING
85
Aston Villa F.C.
16,3%
ING
20
Swansea City F.C.
78,6%
ING
53
A.C. Siena
48,4%
ITA
86
Hamburger S.V.
15,3%
A
21
A.S. Saint-Etienne Loire 
78,2%
F
54
Real Betis
48,4%
E
87
Blackburn Rovers
13,1%
ING
22
F.C. Augsburg
78,2%
A
55
Rayo Vallecano
47,4%
E
88
Chelsea F.C.
12,0%
ING
23
A.C. Milan
77,5%
ITA
56
R.C.D. Español
45,5%
E
89
Villarreal C.F.
11,6%
E
24
Udinese Calcio
77,5%
ITA
57
F.C. Bayern Munich
43,0%
A
90
F.C. Lorient-Bretagne Sud
8,9%
F
25
 A.C. ChievoVerona 
77,2%
ITA
58
Olympique Lyonnais
42,0%
F
91
Hertha B.S.C. Berlin
8,1%
A
26
F. C. Girondins de Bordeaux
76,5%
F
59
O. G. C. Nice
39,4%
F
92
Racing de Santander
6,8%
E
27
Hannover 96
75,1%
A
60
F.C.Sochaux
38,9%
F
93
A.J. Auxerre
4,5%
F
28
S.S. Lazio
74,7%
ITA
61
F.C. Barcelona
38,2%
E
94
Wolverhampton W. F.C.
3,7%
ING
29
S.C. Freiburg
74,0%
A
62
Sporting de Gijón
37,0%
E
95
Liverpool F.C.
2,6%
ING
30
Real Sociedad
72,3%
E
63
Cagliari Calcio
35,6%
ITA
96
Olympique de Marsella
2,5%
F
31
 V.f.B. Stuttgart
70,7%
A
64
Stade Brestois 29
35,5%
F
97
F.C. Kaiserslautern
2,4%
A
32
Fulham F.C.
70,4%
ING
65
S.S.C. Napoli
34,6%
ITA
98
A.C. Cesena
2,3%
ITA
33
West Bromwich Albion
70,1%
ING
66
QPR F.C.
34,4%
ING
Julio del Corral Cuervo es profesor contratado doctor en Economía en la Universidad de Castilla-La Mancha y miembro de la Fundación Observatorio Económico del Deporte.
* Agradezco la ayuda en el tratamiento de la información de Jesús Gómez-Roso, así como los comentarios recibidos de Fernando del Corral.
** Una versión de este trabajo se ha enviado para su posible presentación en el IV Congreso Iberoamericano de Economía del Deporte.

[1] Bueno y un poquito de programación dado que hacer esto a mano es totalmente inviable.

Publicado el

Análisis de las probabilidades de clasificación a cuartos de final de los equipos españoles en la Champions

Ayer terminaron dos semanas horribilis para los equipos españoles en la Champions League. Lo que muchos aficionados se preguntaran ahora es por la probabilidad de que sus respectivos equipos remonten la eliminatoria para así clasificarse para los cuartos de final. Hay básicamente dos enfoques alternativos: 1. Mirar datos históricos y 2. Mirar las probabilidades que otorgan las casas de apuestas.
Consultando la base de datos de las eliminatorias en competiciones europeas de fútbol europeo, puede conocerse las veces que los equipos han remontado habiendo obtenido en la ida los resultados que los equipos españoles. En concreto desde la temporada 1972-1973 hay 250 eliminatorias cuyo resultado en la ida fue 1-2 que fue el resultado obtenido por el Valencia. De estas eliminatorias sólo en 12 ocasiones resultó vencedor el equipo que jugó la ida en casa, es decir que la probabilidad que refleja la historia de una remontada del Valencia es de 4,8%. El Real Madrid obtuvo un empate a 1 gol. En este caso de un total de 525 eliminatorias el equipo local en la ida salió airoso de la eliminatoria en 135 ocasiones, lo que se traduce en un 25,7%. Los equipos españoles que quedaron primeros de grupo tampoco obtuvieron resultados positivos, perdiendo el Málaga por 1-0 mientras que el Barcelona perdió en San Siro por 2-0. El resultado de 1-0 en la ida se repitió 732 veces, de las que en 297 ocasiones el equipo visitante en la ida se aprovechó de la ventaja de campo, lo que se traduce en un 40,6% probabilidades de remontar. Por último, el Barcelona obtuvo el resultado más desfavorable a priori perdiendo por 2-0, sin embargo de las 496 eliminatorias en las que el equipo visitante en la ida perdió 2-0, este equipo remontó en 91 ocasiones, lo que se traduce en una probabilidad del 18,3%.
Alternativamente pueden utilizarse las probabilidades asociadas con las cuotas de una casa de apuestas. Para conocer como pueden ser traducidas las cuotas de las casas de apuestas en probabilidades puede consultarse este otro artículo (http://jdelcorral.blogspot.com.es/2011_09_01_archive.html) . Las cuotas que ofrece la casa de apuestas CODERE de que pasen los equipos a la siguiente ronda son:
PSG: 1,1- Valencia: 6
Manchester United: 1,90- Real Madrid: 1,80
Málaga: 3,55- Oporto: 1,25  
Barcelona: 2,05- Milán: 1,70
Esto se traduce en que las probabilidades de que pasen la eliminatoria los equipos españoles son:
Valencia- 15,5%
Real Madrid- 51,4%
Málaga- 26%
Barcelona-45,3%
Es decir, que esta casa de apuestas considera que las probabilidades del Real Madrid, Barcelona y Valencia son superiores al histórico mientras que la probabilidad de remontar del Málaga es inferior a la de los equipos que obtuvieron su mismo resultado en la ida.
Si creen que el método histórico es el más adecuado para conocer la probabilidad les animo a apostar unos eurillos dado que la mayoría de apuestas son lo que se conoce en el argot apuestas con valor.
Julio del Corral Cuervo es profesor contratado doctor en Economía en la Universidad de Castilla-La Mancha y miembro del Fundación Observatorio Económico del Deporte. La base de datos la ha realizado Carlos Varela al cual le estoy co-dirigiendo la tesis doctoral junto a Juan Prieto.