En este artículo se abordan dos cuestiones. En primer lugar, la eficiencia de los equipos en la primera vuelta de La Liga 2. Por otra parte, se realizan dos tipos de simulaciones: simulación de las posiciones finales teniendo en cuenta los resultados de la primera vuelta, y simular la liga completa con sus 42 jornada asumiendo que las cuotas de la primera vuelta darían la misma información para la primera vuelta y la segunda. Es decir, sería una simulación de las posiciones de la liga al “comienzo de ésta”. Estas simulaciones se usarán para saber qué pueden esperar los equipos a día de hoy y qué podían esperar al inicio de liga. Asimismo, se usa para ver como de hipertensiones es la liga. En concreto, si mirará la diferencia en puntos entre el sexto, último equipo que disputa el play-off y el 19 que es el que baja de categoría con mayor puntuación.
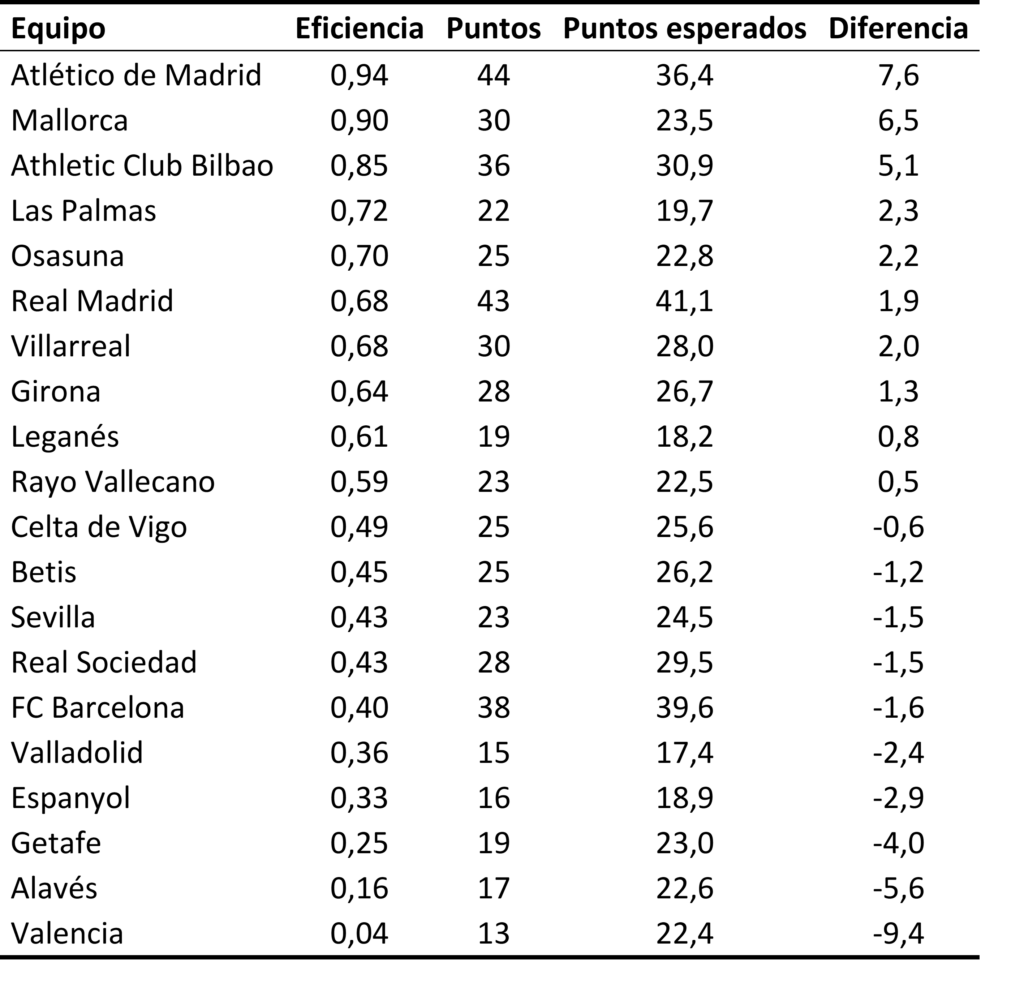
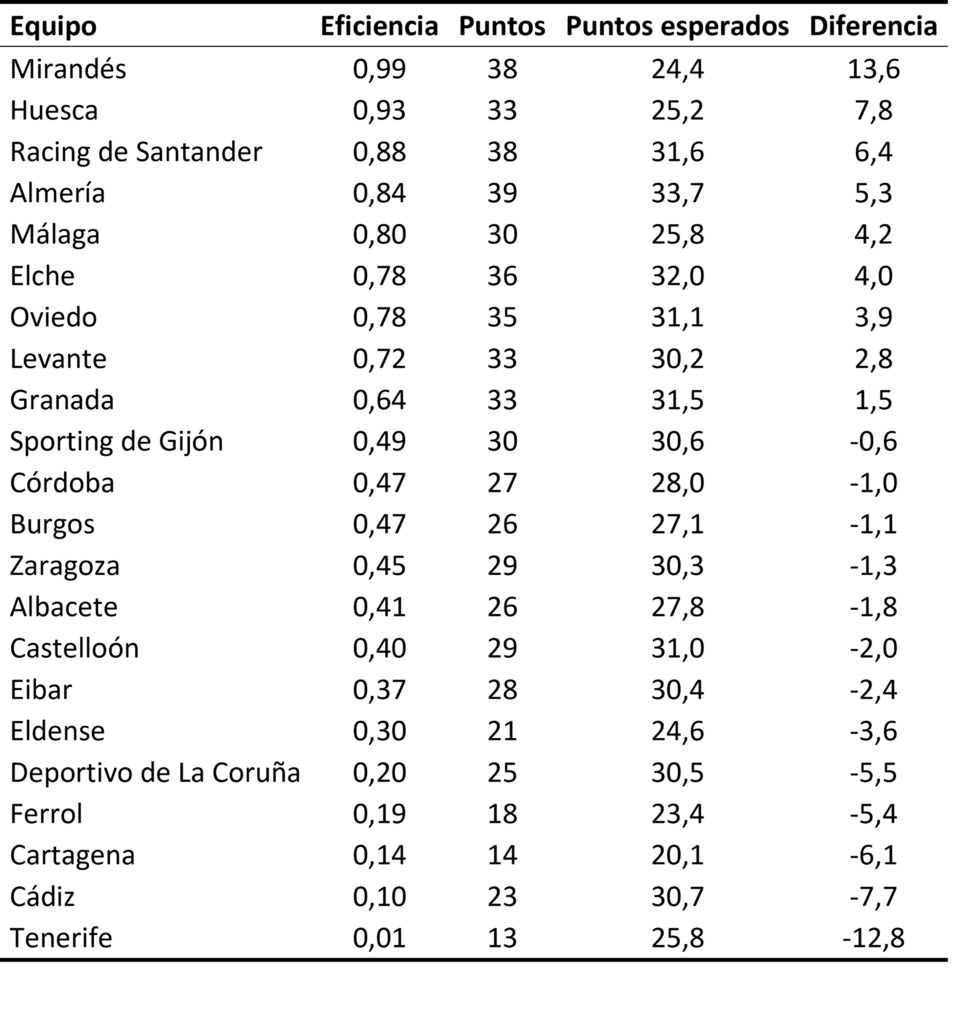
Para calcular la eficiencia de los equipos sigo la metodología de este artículo que proporciona una eficiencia de 1 o próxima a 1 para los equipos que han realizado una temporada muy por encima de sus expectativas según las casas de apuestas, y de 0 o próximo a 0 para los equipos que hayan realizado una temporada muy por debajo de sus expectativas. La siguiente tabla muestra la eficiencia de los equipos. Asimismo, calculo los puntos esperados según las casas de apuestas y la diferencia entre puntos conseguidos y los puntos esperados. Así, una diferencia positiva significa que un equipo ha tenido un rendimiento por encima del previsto.
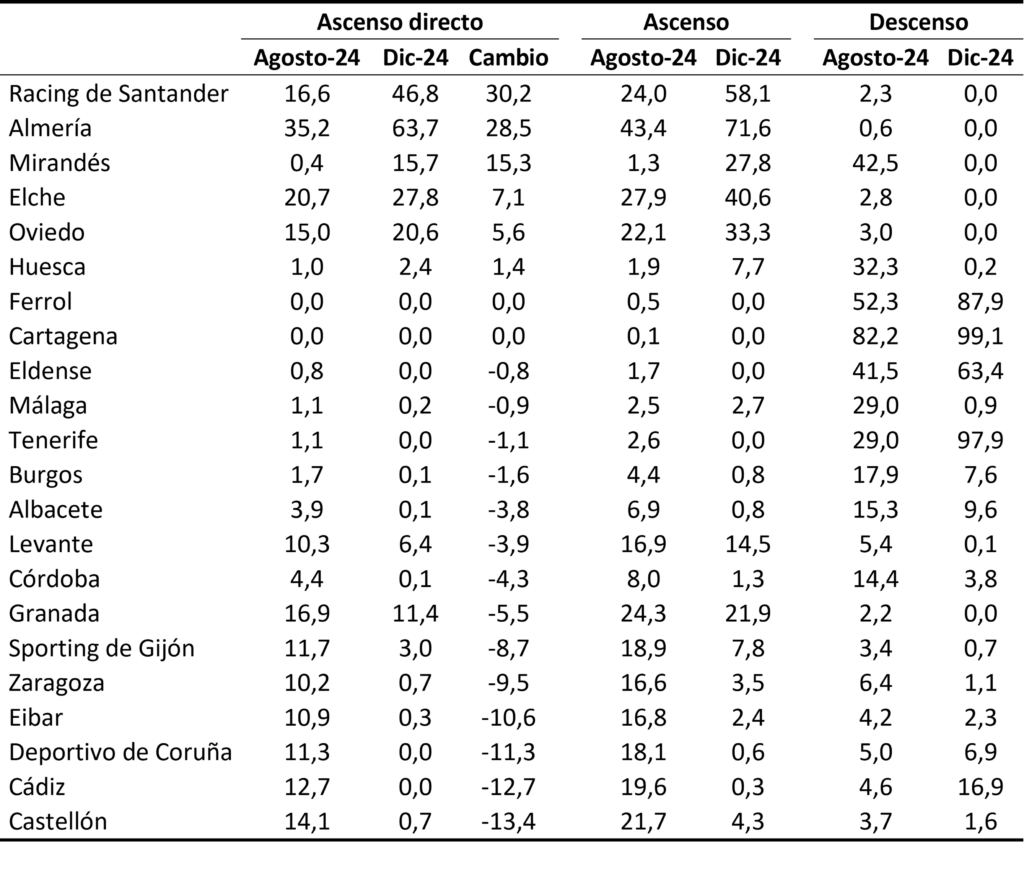
Tabla 1. Eficiencia de los equipos en La Liga 2 primera vuelta 2024-2025
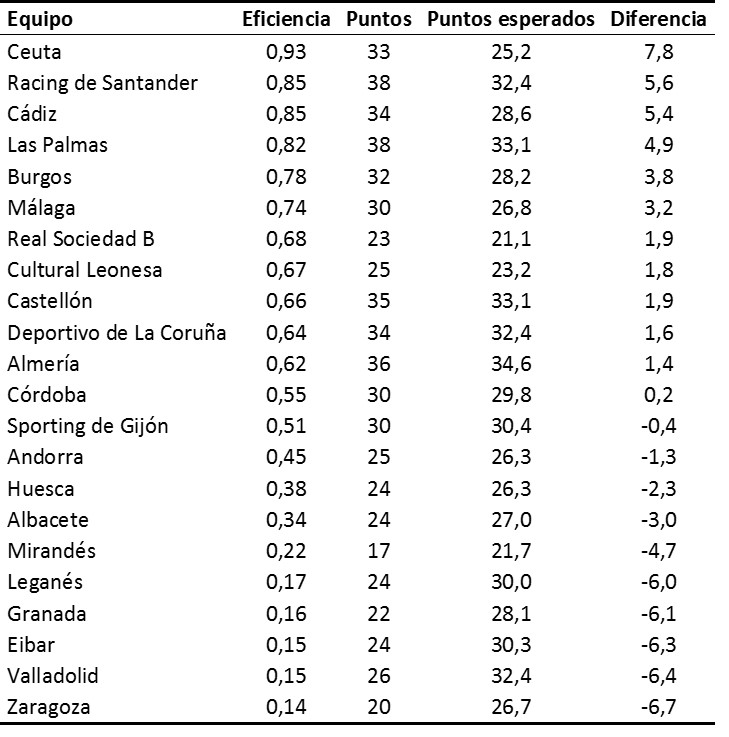
Sin lugar a dudas, el equipo que mejor ha rendido dado lo que se esperaba de él ha sido el Ceuta, que parecía abocado a luchar por evitar el descenso y está peleando las posiciones de honor. Le siguen el Racing de Santander, el Cádiz y Las palmas. Por abajo, Zaragoza, Valladolid, Eibar, Granada y Leganés tienen una eficiencia en torno a 0,15.
Con estos resultados se simula 1.000 veces la segunda vuelta así generando una distribución de probabilidades de quedar en cada una de las 22 posibles posiciones. Las simulaciones usan las cuotas de la primera vuelta para establecer las probabilidades para cada partido y así poder simular los partidos de tal forma de si la probabilidad de ganar del equipo local es 0,8 la probabilidad de que gane el partido en una simulación es del 80%. También se añade información de los resultados de la primera vía sumando un 40% de la diferencia entre puntos conseguidos y puntos realizados. Por último, se asume que en caso de llegar a la fase de ascenso la probabilidad de ascenso es del 25%.
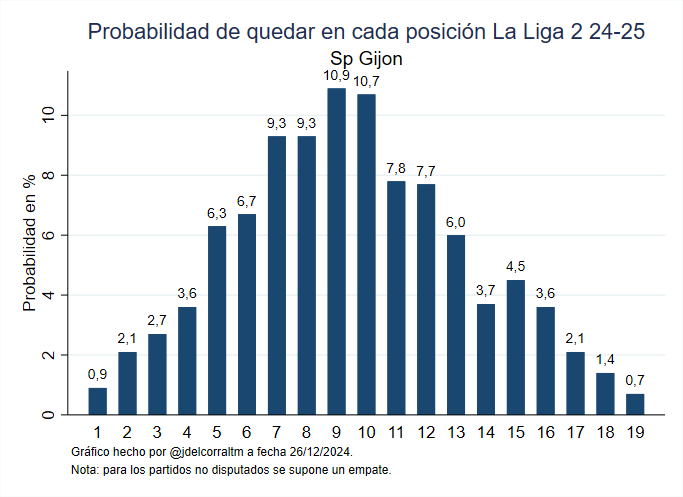
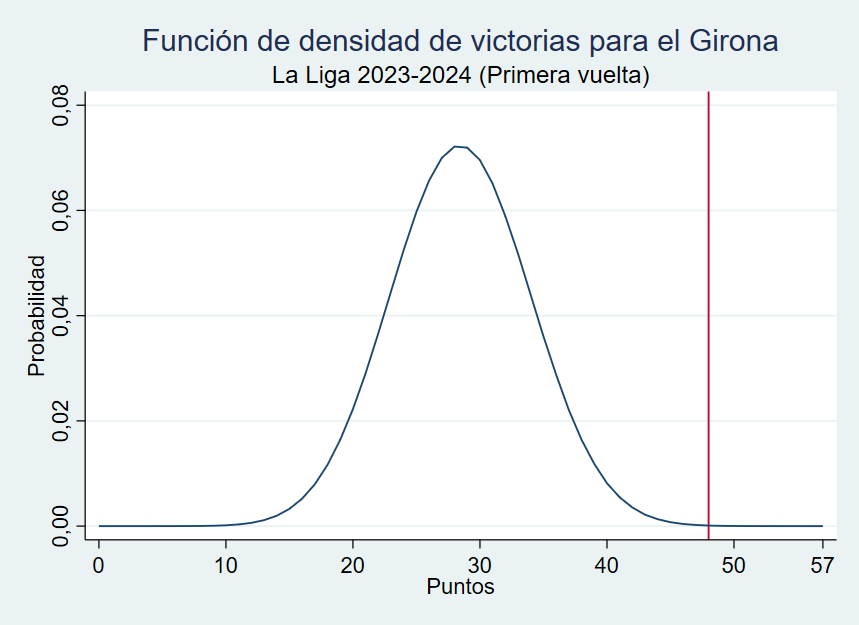
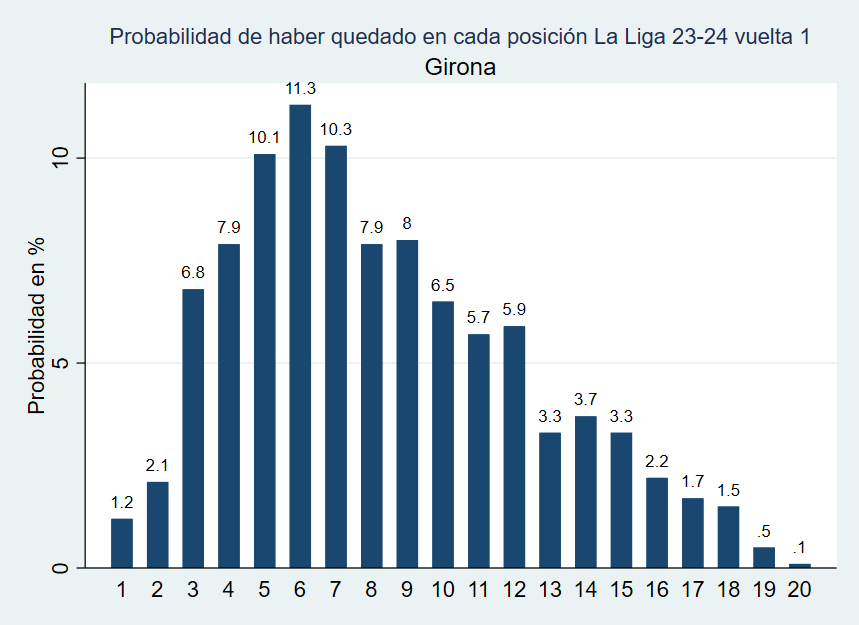
Como ejemplo pongo el gráfico del Sporting de Gijón en el que se puede ver que lo más probable es que se quede en tierra de nadie entre el descenso y la lucha por el ascenso. El gráfico para todos los equipos puede descargarse en este enlace.
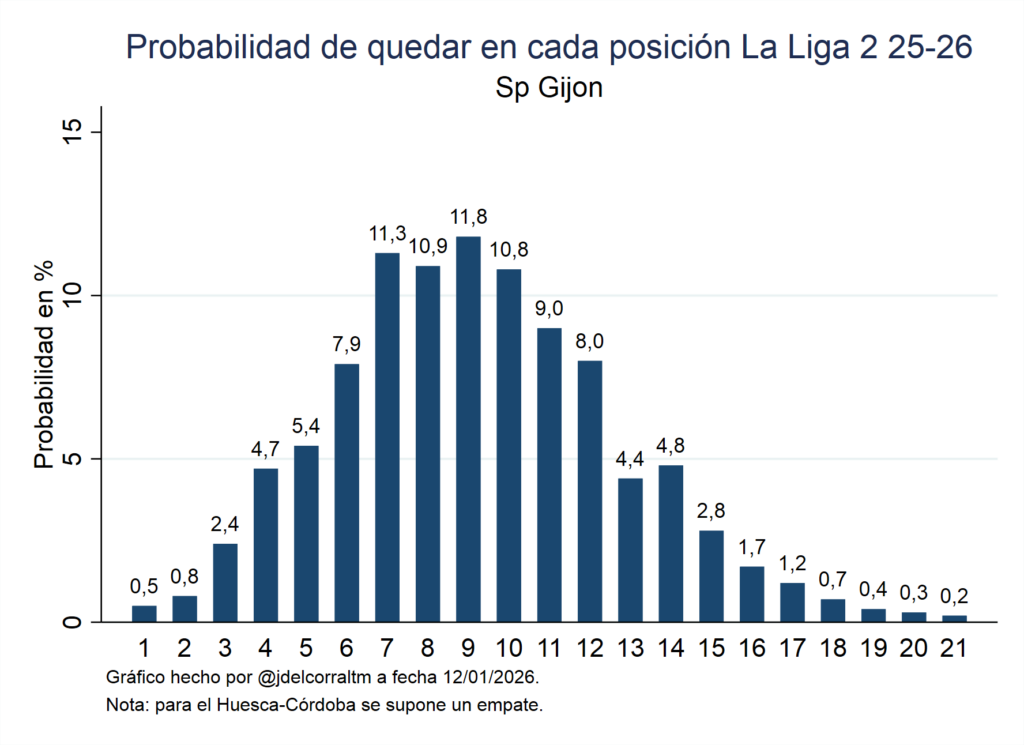
Gráfico 1. Probabilidad de quedar en cada una de las posiciones de La Liga 2 2025-26 del Sporting de Gijón a fecha 12/01/2026.
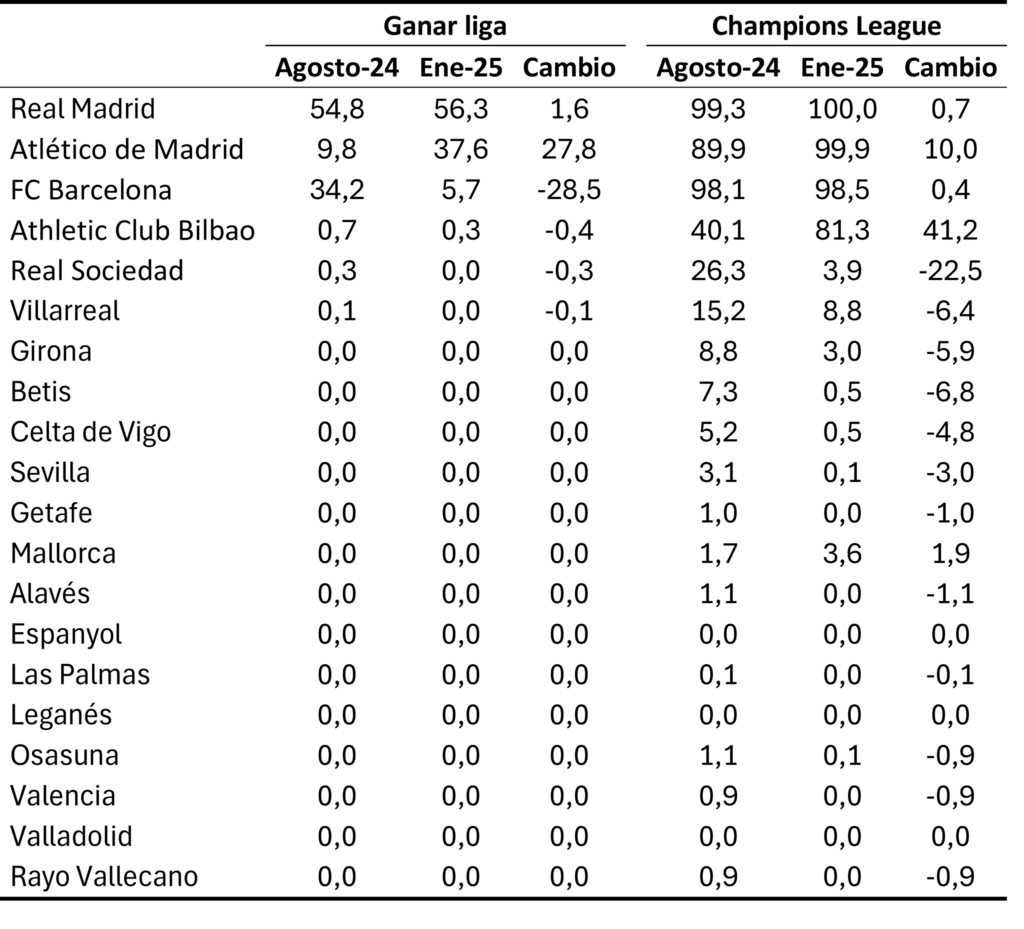
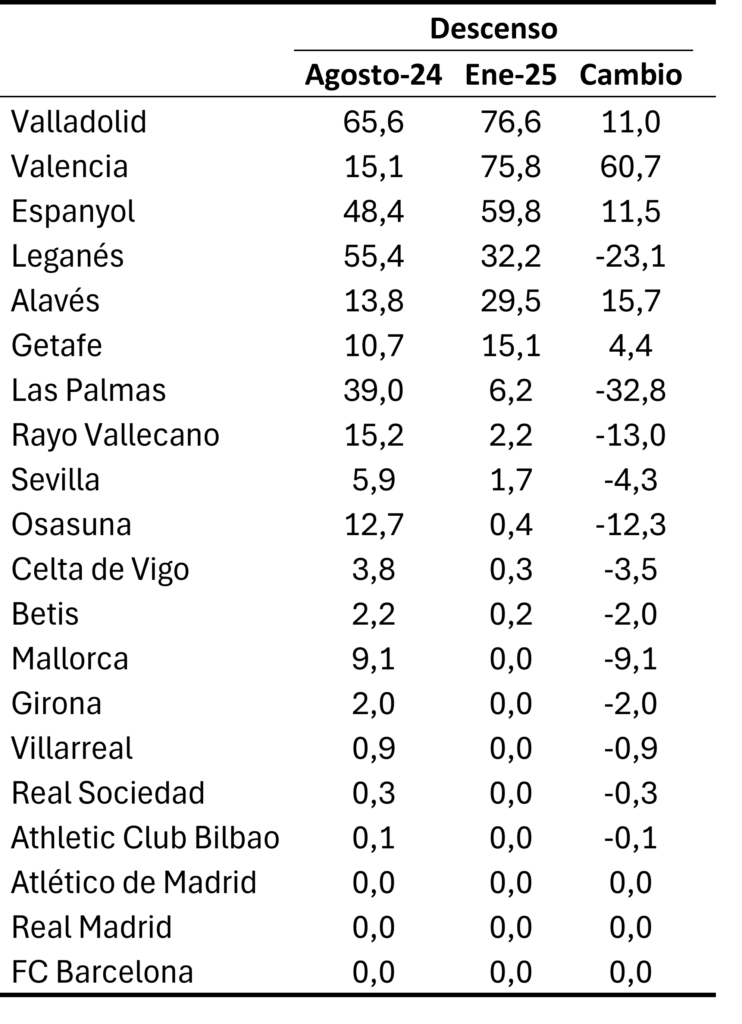
Tabla 2. Probabilidades de ascenso directo, ascenso, descenso La Liga 2 a fecha 12/01/2026
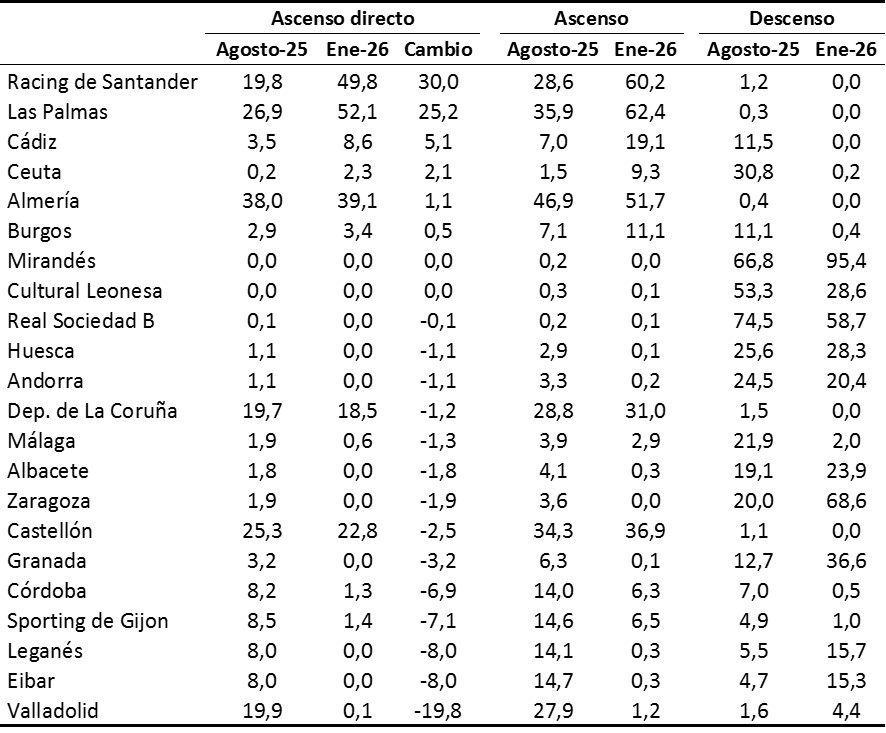
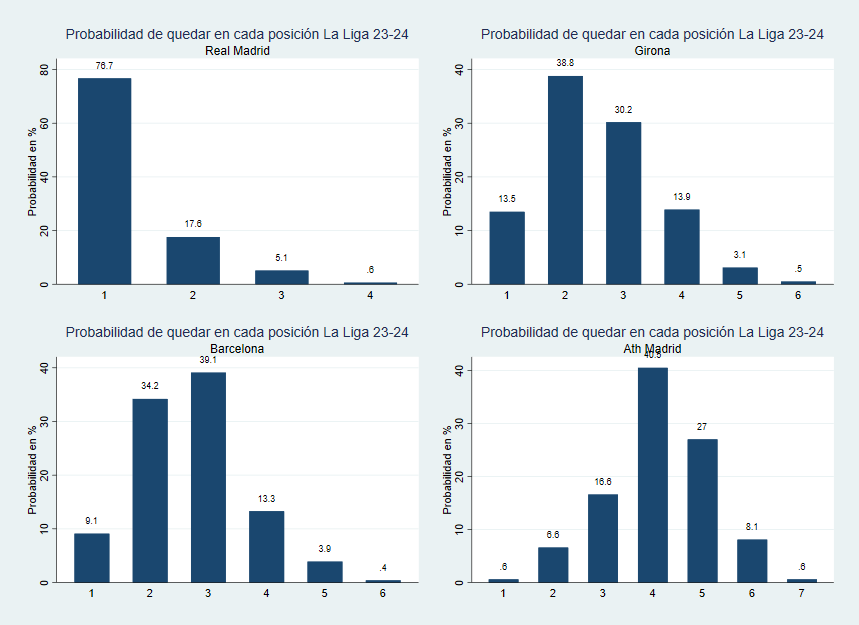
En cuanto a las probabilidades de ascender a día 12 de enero de 2026 destacan Las Palmas (62,4%), Racing de Santander (60,2%), Almería (51,7%), Castellón (36,9%) y Deportivo de La Coruña (31%). El resto de equipos no llega ninguno al 20%. En la lucha por el descenso las simulaciones le da al Mirandés por casi descendido con un 95,4%. El Zaragoza pinta feo con un 68,6%.
En cuanto a los cambios en la probabilidad de ascender trascurrida la primera vuelta puede verse como los grandes beneficiados son el Racing de Santander y Las Palmas aumentando sus probabilidades de ascenso en más de 25 puntos porcentuales.
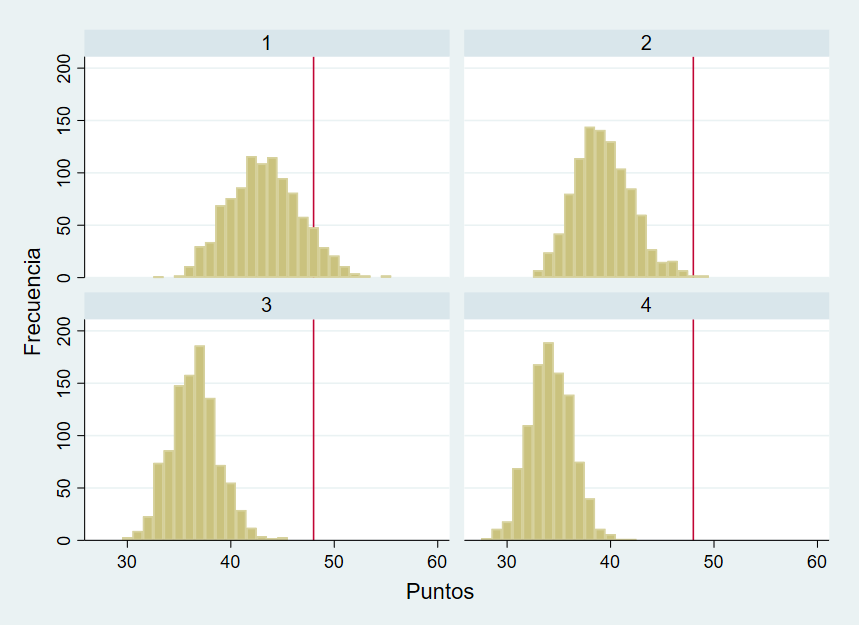
Para concluir vamos a analizar cómo de hipertensiones es La Liga 2. Es decir, cómo de igualada es la liga de tal manera que un equipo pueda estar luchando por evitar el descenso y por conseguir un puesto en play off. Para ello, se mira los puntos que realizan los equipos que quedan en las posiciones p2, p6 y p19 primero. Para después analizar la diferencia entre la p6 y la p19.
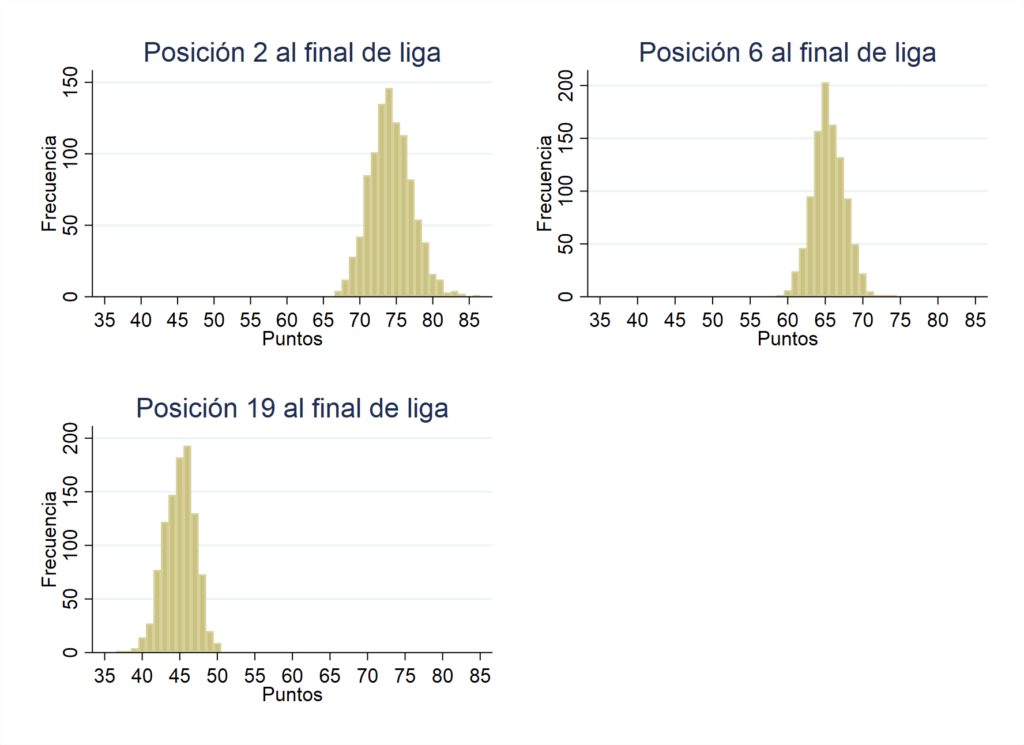
Gráfico 2. Histogramas de puntos para las posiciones p2, p6 y p19 de La Liga 2 2025-26 a fecha 12/01/2026.
El siguiente gráfico muestra los histogramas de la diferencia de puntos entre p6 y p19 tanto simulando lo que queda de liga como simulando la liga completa.
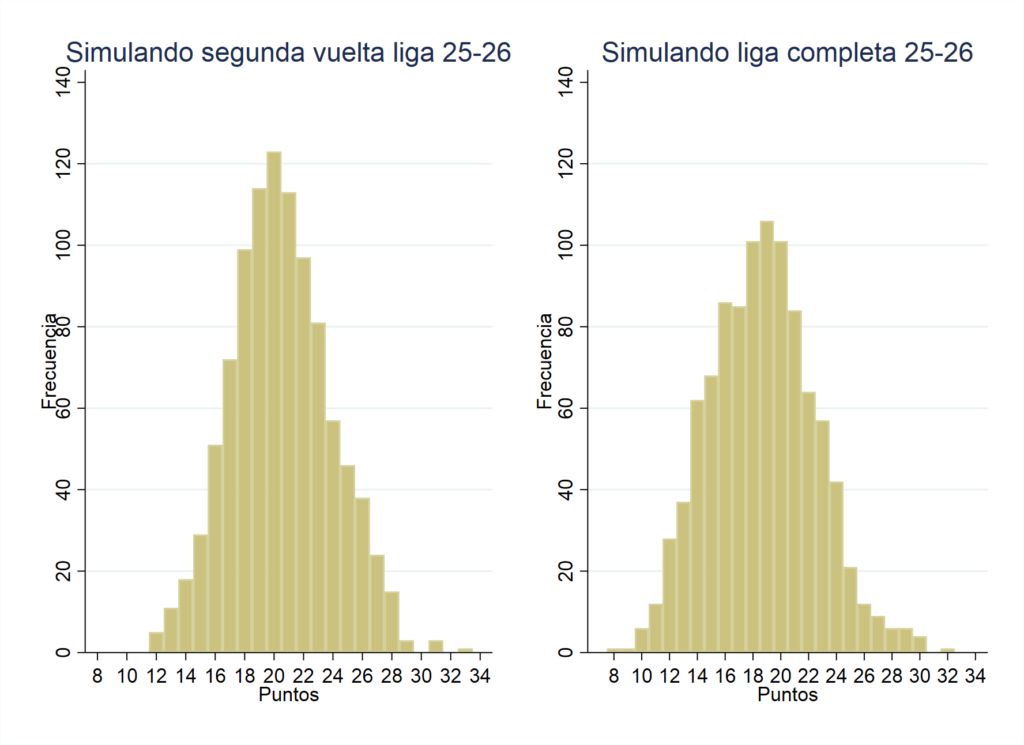
Gráfico 3. Histogramas de la diferencia de puntos entre p6 y p19 de La Liga 2 2025-26.
El resultado de ello es que el promedio de la diferencia entre la p6 y p19 esperado es de 18 puntos. Es decir, un equipo que este en el medio con ganar tres partidos más o perderlos pasa de luchar por ascender a luchar por descender. Simulando la liga completa hay en una simulación de 1.000 que la diferencia es de tan sólo 8 puntos!! Para poner en contexto, por ejemplo, en La Liga 24-25 la diferencia entre entrar en Champions y el descenso fue de 30 puntos. Así que sí, la Liga Hipermotivon es muy hipertensiones.