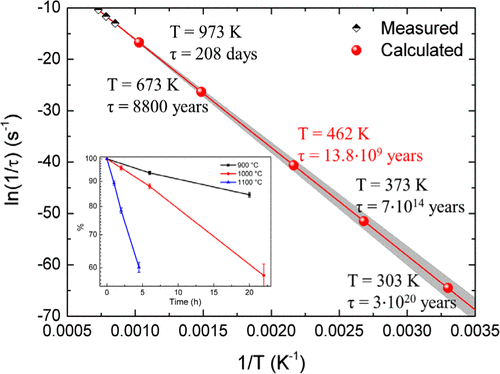
A lo mejor no parece importante, pero un auténtico misterio de la física hasta hace poco era la formación de montones con material granular en caída libre. Es decir, yo dejo caer desde una distancia fija algo en forma granular, y trato de predecir o modelar la forma que tendrá ese montón. Hasta hace algún tiempo había resultados experimentales y teóricos contradictorios, entre otras cosas porque no hay un modelo claro de material granular: El material granular son pequeñas piezas con formas distintas entre sí y no se sabe muy bien cómo modelar ni la forma del grano, ni la interacción entre ellos.
Piensen que el material en forma granular tiene interacciones entre granos o partículas vecinas que los separa del sólido rígido, que es el equivalente a granos formando un auténtico continuo, como en los metales, y del modelo de partículas rígidas separadas, cuando no hay demasiados granos. Un modelo que daba algún resultado decente es adaptar el modelo de sólido deformable y quizás elástico con propiedades constitutivas propias para el material granular. Es decir, se hace una aproximación de un material en estado discreto por un continuo cuya descripción encaja en los experimentos con diversos materiales granulares.
Este tipo de aproximaciones no ha sido capaz de resolver un problema de la generación de montones: que la distribución de presiones en el centro del montón depende de cómo se haya formado el montón, de forma que si se genera desde un sólo punto de caída del material, aparece una depresión en la base del montón; cuando se genera median una «lluvia», es decir desde múltiples puntos de caída del material, la depresión en el centro no es visible. En el artículo PRL – Vol113 – 068001 (2014) se demuestra que el uso de modelos elastoplásticos que no eran capaces de predecir estos dos resultados sí que funcionan, pero si se usa un modelo matemático que tiene en cuenta la historia del fenómeno para la descripción numérica.
Cuando se simula un sistema tridimensional en un ordenador, hay que hacer una malla tridimensional de puntos en la que se calculan las propiedades del material, presión, densidad, fuerzas, etc. Esta malla puede seguir o no al material en su movimiento. Cuando la malla es fija y el material se mueve dentro de ella, podemos tener en cuanta la historia de este movimiento mejor.
El resultado final es que en simulaciones con dos modelos distintos de materiales elastoplásticos, se observa la caída de presión en le centro de la pila o montón que ya fue observada experimentalmente, como la figura tres del artículo muestra:
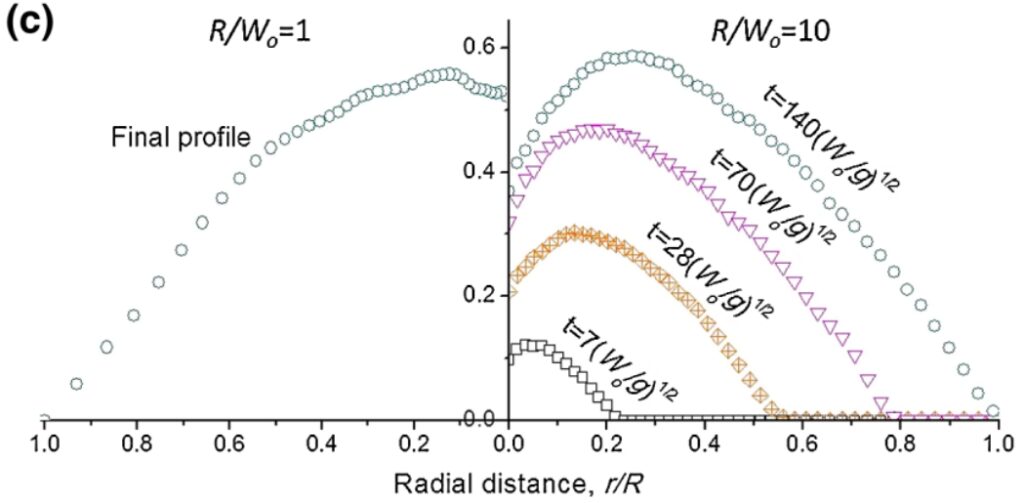
En la figura se muestran los perfiles de presión según el material granular caiga en forma de «lluvia», izquierda, o desde un punto, derecha. Ambos están marcados por la relación entre el ancho de la boca y el radio del montón. En el primer caso, R/W0 es 1. Cuando R/Wo es 10, es decir, todo el material cae desde un sólo punto, se puede observar como según el instante de tiempo en el que observemos el perfil de presiones, éste cambia y termina desarrollando la depresión central al final.