Etiqueta: Física de fluidos

Influencia de la Luna y el Sol en el movimiento de las plantas.

Se supone que la influencia gravitatoria combinada del Sol y la Luna puede producir movimientos en la plantas, pero hasta ahora no se ha podido cuantificar ni entender el mecanismo subyacente, más allá de estimar que será un efecto de cambios en la gravedad de la superficie debido a la rotación de la Tierra. El artículo que comento precisamente demuestra, mediante datos obtenidos de experimentos previos realizados en la estación espacial y modelos analíticos, que la influencia de estos dos astros en el movimiento de las plantas se puede entender gracias a las inestabilidades de Rayleigh-Taylor debidas a cambios en la gravedad por al rotación en el sistema circulatorio de la planta.

Comienza la introducción del artículo diciendo que esta influencia gravitatoria sobre el movimiento de las planta está muy cuestionada, incluso hay quien la niega o considera que es sobre todo, un ritmo circadiano(1) esencialmente controlado por la luz u otro factor. Pero en este artículo demuestra la influencia del Sol y la Luna en los movimientos de las plantas, usando datos recabados del movimiento de plantas en la estación espacial como caso especial.

Para empezar, señala en la introducción que los movimientos de las plantas en la Tierra siguen un periodo de 24,8 horas, mientras que algunas plantas que se subieron a la estación espacial tenían un periodo de 45 minutos, cuando la rotación de la estación es de 90. Comentan que está demostrado que las modulaciones del campo gravitatorio de la Tierra debido a la acción del Sol y la Luna se ha demostrado que influye en el crecimiento de las plantas, y que puede llegar a ser percibido por otros seres vivos.

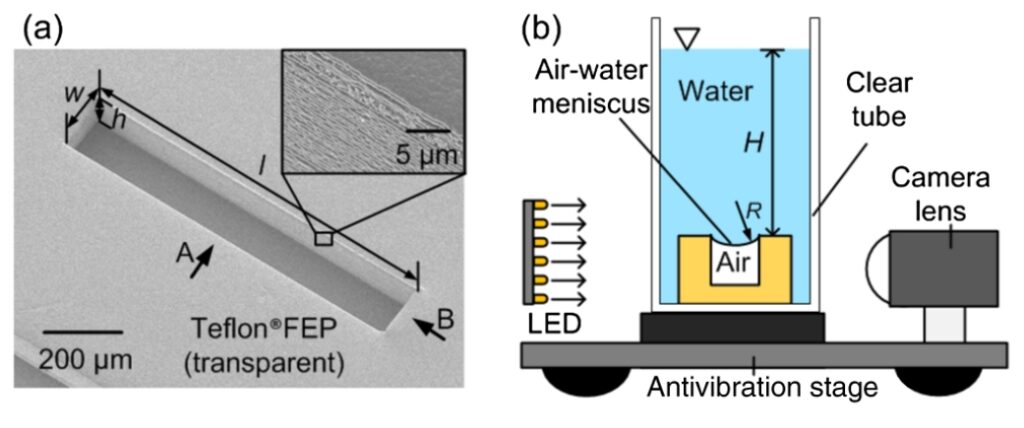
Para tratar de entender bien estos efectos, el autor del artículo desarrolló unos modelos simplificados del sistema circulatorio del las plantas, tubos microscópicos y de tamaño milimétrico, mesoscópicos, que contenían savia y un gas. En el artículo no lo especifica, pero tiene sentido que el gas sea aire atmosférico.

Para que la gravedad y la separación entre el líquido, la savia, y el gas pudiera tenerse en cuenta, estudió los tubos en horizontal y en vertical. Los tubos en horizontal serían equivalentes a las raíces de las plantas y los tubos en vertical, a los tallos.

Cuando los tubos están en horizontal, las raíces, debido al pequeño tamaño de los tubos empleados, la savia ocupa toda la superficie de los mismos, dejando el gas en el centro, de tal forma que hay una interfaz líquido-gas de simetría radial. En los tubos que hacen de tallos, debido a una ley denominada en el artículo como ley de Jurin(2) que relaciona la altura de un líquido por un tubo fino con su diámetro, se termina formando una interfaz líquido-gas en el punto de máxima altura de la savia.

Ambas interfaces líquido-gas se pueden estudiar como un caso especial de la inestabilidad de Rayleigh-Taylor, que el artículo afirma permite predecir, y demostrar con los datos experimentales de la estación espacial, la frecuencia de movimiento de las plantas, dado que el efecto más importante es el de la gravedad del Sol y la Luna a través de resonancias paramétricas asociadas con la variación de la gravedad.

Sigue el artículo con una sección que dedica a la estabilidad de las superficies líquido-gas en los tubos. Concretamente, plantea un modelo que permite definir las variaciones en la interfaz entre savia y gas para los tubos horizontales, despreciando los efectos a segundo orden y considerando que los dos fluidos son incompresibles y los efectos de la viscosidad despreciables. El resultado final es que las variaciones en esa interfaz líquido-gas tienen una frecuencia que se puede deducir de la ecuación que relaciona la diferencia de presiones entre líquidos y gas(3).

De esta ecuación se puede obtener una relación entre frecuencia de perturbaciones y magnitudes materiales del líquido y gas, densidad y viscosidad, que emplea en la sección siguiente para dar valores numéricos a las características de los fluidos, además de considerar qué fórmulas y modelos pueden emplearse según los tubos estén en horizontal o vertical en la Tierra o en al estación espacial.

En las dos secciones siguientes estudia las variaciones del valor de la gravedad en la Tierra y la estación espacial, dándole un valor numérico a la oscilación, que es pequeñísima, del orden de 1/ 8 000 000 en la Tierra.

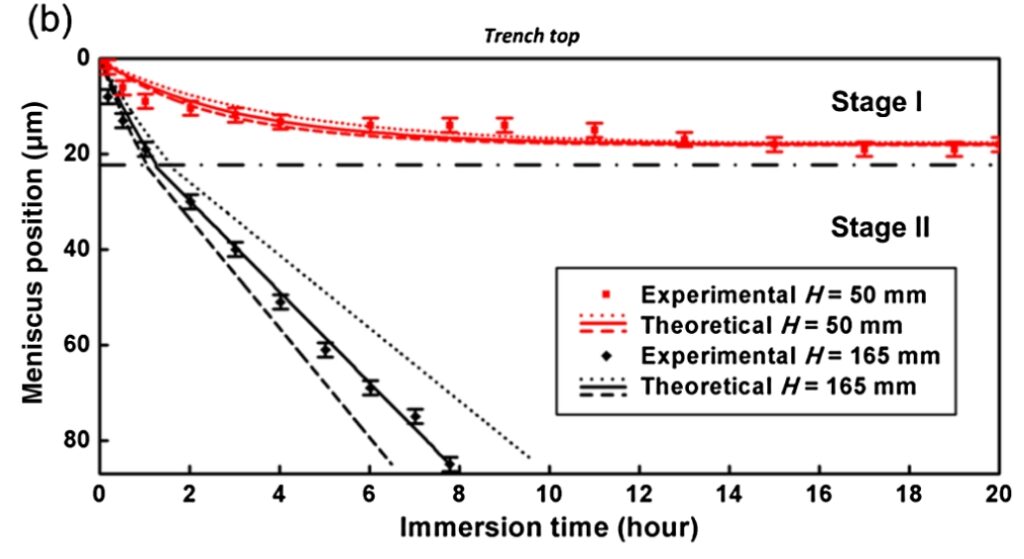
En la sección siguiente comienza con una muy breve introducción a la ecuación de Mathieu, una ecuación diferencial que aparece con muchísima frecuencia en el estudio de la estabilidad de sistemas con cambios oscilatorios en algunas magnitudes. Luego, aplica las relaciones y formas anteriores a las resonancias que provoca la gravedad de la Luna y el Sol tanto en la Tierra como en la estación espacial en el valor de la frecuencia que aparecía en la ecuación de la diferencia de presiones de la interfaz. Así, logra demostrar que estas oscilaciones periódicas tienen las mismas frecuencias observadas en los movimientos de las plantas en los dos lugares, al comprobar como el periodo de las mismas coincide con el predicho según esta teoría de la inestabilidad de Rayleigh-Taylor, demostrando la influencia de la gravedad en los movimientos de las plantas.

Es enormemente curioso que los movimientos de las plantas tengan una relación tan estrecha con las oscilaciones tan pequeñas en la gravedad debidas a la Luna y el Sol, en función de la rotación terrestre. Mi corazoncito ciencaficcionero no puede por menos que notar que en otros planetas, con ciclos de rotación diferentes, estos movimientos de las plantas también serán muy distintos.

El artículo salió publicado en la revista Physics of Fluids, volumen 32: Phys. of Fluids. DOI:10.1063/5.0023717

(1) Ritmo circadiano: es el ritmo interno de las diversas variables que se midan en un ser vivo, desde composiciones químicas hasta periodos de actividad, asociadas a cambios externos. El enlace de la wikipedia en español es bastante ilustrativo: Wiki: Ritmo Circadiano

(2) James Jurin: Un médico londinense que efectuó estudios estadísticos muy importantes sobre la viruela, además de estudiar el efecto de la capilaridad en los líquidos. El artículo de la wikipedia en español es bastante bueno: Wiki: James Jurin

(3) No puedo poner bien la ecuación porque el sistema que empleo para escribir no tiene editor de ecuaciones. Malamente, la ecuación tiene la forma: d(p²)/dt^2 + w*p =0. Donde p es la diferencia de presiones y w la frecuencia.

Capa de invisibilidad para ondas en el agua

Además de por su propio interés científico, hay razones extra para querer lograr que las ondas en el agua, las olas, desaparezcan en un determinado terreno, que es de lo que trata el artículo que comento aquí. Cuando se hacen puertos y estructuras del estilo, donde los barcos deben atracar, el oleaje que se forme es muy molesto, por eso se suelen poner barreras capaces de minimizar el mismo. Pero si hay olas muy grandes, pasan por encima de las barreras y por lo tanto, los barcos no pueden atracar y los que están atracados se mueven, con todos los riesgos de seguridad que eso conlleva.

Los autores del artículo comienzan en su introducción comentando la importancia de los océanos para la humanidad, dado que los empleamos como rutas de transporte y lugares de alimentación y recreo(1). Y dado que el mar es de todo menos tranquilo, la investigación sobre sistemas de control del oleaje es un campo muy activo de la hidrodinámica. Como comentaba en el párrafo anterior, métodos más habituales de control del oleaje logran su disipación o atenuación, pero no su eliminación. Por eso con los sistemas actuales podemos o bien disminuir la altura de las olas o bien la frecuencia con la que llegan cerca de los puertos, pero no eliminar por completo el oleaje.

Sin embargo, en el campo de ondas electromagnéticas, y gracias al uso de metamateriales(2), el lograr la atenuación de estas ondas en volúmenes muy concretos, o su paso sin perturbar las ondas en sí, ya se ha conseguido en diversas condiciones. Por supuesto, algo así sería muy ventajoso en estructuras humanas cercanas al mar, porque si las olas pasan a través de un volumen determinado sin que se note su presencia, no pueden afectarlo ni a los barcos que contiene. Según el artículo, los problemas principales de estos metamateriales para su aplicación a las ondas marinas son dos. El primero, que las estructuras que hay que hacer son muy complejas, lo que dificulta su replicación en puertos y demás. Además, generalmente su función de invisibilidad o paso de una onda sin verse afectada por ella sólo la cumplen para una longitud de onda, cunado las olas son ondas de muy amplio espectro. Con estos dos inconvenientes, no se podrían emplear las estructuras actuales para su uso con ondas en líquidos.

Comentan después los investigadores que el uso de metamateriales en gradientes planos soluciona algunos de estos problemas: son estructuras que se pueden replicar en el tamaño requerido, relativamente fáciles de montar y que tiene un ancho de banda grande, lo que permitiría que atenuaran un conjunto grande de oleajes. Su uso en óptica está restringido, en el sentido de que más que trasladar la onda sin alterarla, este tipo de gradientes eliminan la amplitud que entre, atenuando muy fuertemente la onda electromagnética. Pero es este el objetivo de los autores con la olas: eliminarlas en una región dada.

Así, los autores adaptaron la tecnología de metamateriales con un gradiente de índice o GIM en inglés(3), para lo que en lugar de usar diversos materiales, emplearon distintas profundidades como generadores de diversos índices de transmisión de las ondas marinas en el agua. Con algo tan sencillo de construir como diversos gradientes de profundidad en el agua, se induce la «invisibilidad» de una zona de la costa a las olas, efectivamente protegiéndola frente a ellas.

La figura siguiente muestra el dispositivo de prueba en un canal:

Como se observa, el gradiente de altura se genera en el comienzo y el final del elemento, mientras que la zona central del mismo es simplemente un paralelogramo plano de longitud L2, anchura t y altura d. Con este sistema, y siguiendo el formalismo de transmisión de ondas que se emplea con las ondas visibles, al pasar por este dispositivo, las ondas marinas «ven» un índice de «refracción» de perfil cambiante en la longitud de propagación n(x).

Estructura de metamaterial con gradiente de profundidad que es capaz de eliminar olas. La figura (a) es un dibujo transversal de algunas dimensionas básicas, la figura (b) muestra el modelo teórico que se empleó y la (c) la realización práctica del mismo. Tomado de la figura 1 del artículo citado.

Es interesante notar que, dado que tenían que trabajar en un canal, las olas las crearon artificialmente con un dispositivo colocado antes del gradiente de alturas.

Como explican con más detalle en el artículo, generalmente las relaciones entre el índice de refracción del material por el que se propaga la onda y la onda en sí genera la dispersión de las ondas, lo que en este caso se traduciría en ondas un poco más pequeñas distribuidas por el canal. Sin entrar en detalles más técnicos, su estructura es capaz de modificar esta relación para permitir que las ondas pasen por el canal fuertemente atenuadas, es decir, en lugar de dispersar las olas, el gradiente de altitud equivalente al GIM deja que la onda se propague atenúandose muy fuertemente, por lo que se evita el problema de las olas.

La siguiente figura muestra el resultado experimental en el canal anterior con ondas de 0,7 Hzs de frecuencia y una altura media del canal de 16 cm:

Eliminación experimental de las ondas para las condiciones vistas arriba. La escala que va de 4 a -4 indica amplitud de la onda, y se observa con claridad como las ondas quedan atenuadas dentro de la zona con el gradiente y después del mismo.Los puntos (b) y (c) son los puntos en los que posteriormente caracterizan la altura de las olas respecto al máximo inicial. Adaptado de la figura 2 del artículo citado.

Antes de iniciar el experimento, simulaciones empelando el método de elementos finitos confirmaron que efectivamente, la geometría del canal anulaba las ondas enviadas. Es fácil ver que después del paso por la zona de gradientes, una cierta parte de las olas se recupera, pero dentro de ese canal, no hay apenas alteraciones de la altura. Sería esa zona la de «invisibilidad» para las olas, donde cualquier objeto situado en ellas no se movería.

Las pequeñas olas que se muestran en los experimentos dentro del canal se deben sobre todo, a efectos no lineales(4) de la viscosidad, que en el modelo analítico que resolvieron de la propagación de las olas, no se tuvieron en cuenta.

Para caracterizar el funcionamiento de este sistema a diversas frecuencias y amplitudes, midieron en los puntos (a), (b) y (c) de la figura anterior la amplitud total de las olas y la dividieron por la máxima a la entrada en el dispositivo, obteniendo una medida directa de la atenuación de las olas en el dispositivo de gradiente variable.

Los datos, que se muestran en la figura siguiente,confirman que para varias longitudes de onda y frecuencias del oleaje artificial el dispositivo funciona, dado que atenúa de manera clara el oleaje.

Disminución de amplitud dentro del gradiente respecto a las olas externas para diversas amplitudes (izquierda) y frecuencias(derecha) de las olas de entrada. El color azul indica que los datos de amplitudes se tomaron en el punto (c) de la imagen anterior, mientras que los rojos en el punto (b). Las estrellas indican valores simulados y los puntos, experimentales. Es fácil ver que para todas las frecuencias y amplitudes medidas, la zona del gradiente atenúa claramente las olas. Adaptado de la figura 3 del artículo citado.

Después de comentar brevemente los resultados de sus experimentos y los límites debidos a los efectos no lineales, concluyen el artículo diciendo que este tipo de gradiente podrían usarse en el diseño y construcción de puertos que permitieran tener aguas tranquilas, casi independientemente de las condiciones del mar.

El artículo salió publicado en la revista Physical Review Letters, en el volumen 123. Su título es: «Broadband Waveguide Cloak for Water Waves»

Notas:

(1) Como ejemplo, en el año 2011 en los Estados Unidos, el 53% de las importaciones y el 38% de las exportaciones entraron por mar, mientras que en el conjunto de la Unión Europea, cerca del 45% de las exportaciones y el 55% de la importaciones ase realizaron por transporte marítimo. Fuentes: EEUU: Bureu of Transportation Statistics. UE: Eurostat.

(2) Los metamateriales son objetos artificiales estructurados diseñados con sus propiedades finales en mente, formados por conjunto de materiales muy diferentes entre si. Es decir, la mayoría de los materiales que se emplean por los seres humanos tiene algunas propiedades deseables y otras no tanto, con las que hay que lidiar de la mejor manera posible. Con los metamateriales, se diseña desde el principio las características que se desean. Una explicación muy buena está en la Wikipedia en inglés: Wiki:Metamaterial.

(3) Metamateriales con gradiente de índice son materiales cuya estructura les causa tener un índice de refracción que varía de forma contínua en el espacio del metamaterial. Como el índice de refracción controla como se propaga la luz para todas las frecuencias, al variar el índice de refracción, se varía la transmisión de la onda electromagnética de la luz. Así se logra «atrapar» la luz en zonas específicas o alterar su transmisión a través de una fibra óptica.

(4) No linealidad: Generalmente, cundo un fenómeno físico tiene que representarse con funciones que no pueden ser aproximadas por una recta, su uso y predicción se vuelve mucho más complicado porque pequeños cambios en los valores llevan a grandes efectos, difíciles de computar o calcular.

¿Contagiamos más enfermedades al hablar más alto?

Dados los tiempos que estamos viviendo, se está produciendo una cantidad enorme de publicaciones relacionadas con enfermedades de transmisión aérea. Una que me ha llamado la atención es este artículo de la revista Scientific Reports, perteneciente a la familia de Nature, que explora la posibilidad de contagios simplemente hablando, por contraste con los métodos más conocidos de estornudar y toser.

Comienzan en la introducción comentando que es bien sabido que la transmisión de enfermedades infecciosas a través de toses, estornudos y respiración es un fenómeno ya reconocido, pero en el que la importancia relativa de estos fenómenos en la propagación de enfermedades es un tema que no está claro.

Explica que al hablar y respirar emitimos partículas de un diámetro medio de 1 µm, probablemente formadas por fenómenos de ruptura de película fluida en los bronquiolos pulmonares(1) y vibraciones en la laringe. Aunque parezcan pequeñas, estas partículas son capaces de llevar con ellas bacterias y otros agentes infecciosos, dado que estos últimos tiene unos tamaños aún más pequeños, del orden de 0,050 a 0,500 µm para el virus del sarampión, por ejemplo.

Al ser más pequeñas, estas partículas tiene el potencial de ser aún más infecciosas que las más grandes, por tres razones principales:

  1. Las partículas más pequeñas aguantan más tiempo suspendidas en el aire,
  2. al ser más pequeñas pueden penetrar hasta distancias más grandes dentro del sistema respiratorio de otra persona distinta del que la emitió y
  3. el número de partículas pequeñas generadas al hablar puede ser muy superior a la que se produce al toser.

Según los autores del artículo, es este último punto el más importante. Tiene sentido: para que cualquier enfermedad pueda infectar un cuerpo, es necesario que la cantidad de virus o bacterias sea tan grande que las defensas del cuerpo no sean capaces de evitar su proliferación descontrolada en el mismo.

De hecho, dedican un párrafo a relatar la gran cantidad de evidencias que demuestran que hablar produce muchas más partículas que toser, lo que incrementa la «eficacia» del habla como portador de enfermedades.

Continúan comentando que, sin embargo, quedan varias cuestiones sin resolver: ¿afecta el volumen de lo que se dice a la generación de gotas?, ¿importas los fonemas que emitamos, es decir, la pronunciación de lo que decimos?, ¿hay diferencias significativas entre individuos? Para tratar de resolverlas, en este trabajo emplearon un sistema experimental capaz de contar las partículas desplazadas por el aire y lo emplearon para contar y medir las mismas mientras varios voluntarios hablaban.

Sus principales conclusiones son:

  1. la cantidad de partículas emitidas se incrementa según el volumen de lo que se diga, en los cuatro idiomas que usaron como representativos(inglés, español, mandarín y árabe)(2),
  2. la distribución del tamaño de las partículas es independiente del volumen con que se hable y
  3. hay algunas personas que emiten una cantidad un orden de magnitud superior a la media, diez veces más, de forma que son «superemisores» de partículas al ambiente.

Este último punto sobre todo, explicaría el fenómeno de los supercontagiadores, las personas que por alguna razón son capaces de contagiar a muchas más personas a su alrededor de lo que es habitual.

En la sección siguiente del artículo, donde explicitan los resultados, lo primero que hacen es repetir experimentos anteriores para confirmar que efectivamente, hablar provoca un aumento de emisión de partículas por parte del hablante. Como indica la figura siguiente, donde simultáneamente se presentan los resultados de un micrófono recogiendo a un voluntario diciendo algo así como «a» durante unos segundos, respirando por la nariz después y volviendo a hablar, es totalmente cierto.

Relación entre la emisión de un sonido, panel A y emisión de partículas, panel B, en el tiempo. Los picos de emisión de partículas son claros, con el retraso entre el máximo del pico y el comienzo del sonido atribuido al tiempo que tardan las partículas en llegar al detector. De la figura 1 del artículo citado.

Después, comprobaron que había una relación entre el número de partículas emitidas y el volumen de lo que se habla. Como muestra la siguiente figura, donde se reúnen datos de muchos sujetos, la relación es linealmente proporcional entre el número de partículas emitidas y el volumen de voz, medido mediante la amplitud del sonido recogido por el micrófono.

El número de partículas emitidas respecto a la amplitud empleada, medida como su media cuadrática(3). Como se puede observar, la relación es una línea recta bastante clara. De la figura 3 del artículo citado.

Como además comprobaron que el tamaño de las partículas emitidas no cambiaba con el volumen de lo que se decía, los investigadores concluyen que la cantidad de líquido emitido aumenta con el volumen de voz.

Los resultados obtenidos indican que no hay diferencias significativas entre los diversos participantes a la hora de emitir aerosoles o partículas. Como escogieron un grupo diverso de voluntarios, con diversas características físicas, como el índice de masa corporal u otras, deducen que no hay correlaciones claras entre «tipos» humanos y la capacidad de emisión de partículas. Tampoco se observaron diferencias importantes entre usar diversos idiomas, siempre que se hablen en el mismo tono de voz. Además, las condiciones de temperatura y humedad externas tampoco influencian de manera significativa la emisión de partículas.

Pero, si todos los participante emiten más o menos e mismo números de partículas, ¿cómo es que hay algunos que son «superemisores»? Pues porque sus propios datos indican que hay un grupo pequeño pero importante, en sus experimentos ocho de cuarenta, que emiten siempre un orden de magnitud más de partículas que los demás: esos son los superemisores. De echo, al comprobar la emisión de partículas en función del tipo de respiración o del volumen de lo que se habla, los superemisores se destacan con claridad, como se ve en la figura siguiente.

Número de partículas emitidas según la actividad del sujeto. En blanco, los diversos tipos de respiración (Nose, nariz, Mouth, boca, Deep-Fast, Inspiración lenta, aspiración rápida, Fast-Deep, Inspiración rápida, aspiración lenta) y en el otro color, los diversos tipos de habla (Quiet, bajo, Intermediate, normal, Loud, alto). El incremento de partículas emitidas al hablar es muy claro, como también la presencia de los superemisores, las dos cruces rojas. De la figura 5 del artículo citado.

En su sección de discusión los autores se preguntan porqué obtienen estos resultados. Empiezan diciendo que parece que, dado que al hablar activamos las cuerdas vocales, es debido a ellas que se produce el incremento de partículas, lo que implicaría que al aumentar el volumen de voz, como también aumenta ligeramente la frecuencia del habla, debería por lo tanto incrementarse el número de partículas. El problema es que para aumentar el volumen de voz, también se incrementa el flujo de aire a través del sistema respiratorio, lo que también contribuiría al aumento del número de partículas. Los investigadores concluyen que de sus datos no pueden desacoplarse los dos efectos ni su importancia relativa.

Pasan después a tratar de entender la razón de la presencia de los superemisores, diciendo que si bien pudiera ser que haya diferencias en en las propiedades de los líquidos en sus sistema respiratorio que sean capaces de provocar este aumento, no han podido analizar nada de este tema. Sí comentan que alteraciones en la químicas de las mucosas del sistema respiratorio, por ejemplo con un nebulizador de agua salada, influyen claramente en la cantidad de gotas emitidas en la respiración o el habla. Concluyen ese párrafo formulando la hipótesis de que son estos superemisores la causa de que haya algunas personas capaces de contagiar enfermedades que se propagan por el aire de manera muy superior a la mayoría, fenómeno bien contrastado y comprobado en general, y en particular en la pandemia de COVID actual.

Comentan también que el hecho de que se incremente de manera muy notable la cantidad de partículas al hablar debería tener una influencia clara en la capacidad de contagio de diversas enfermedades según el lugar donde se alojen los patógenos. Así, comentan que hay evidencias de que la tuberculosis alojada en la garganta es más contagiosa que la que se encuentra en los pulmones y que el virus de la gripe puede ser tan contagioso porque ataca preferentemente la garganta, desde donde al hablar se emiten más partículas.

En el último párrafo del artículo explican que dado que el volumen de lo que se diga tiene una influencia tan fuerte en la cantidad de partículas emitidas, ello implica que los lugares más ruidosos serán fuentes más probables de contagios que los lugares más silenciosos. Y a mí no deja de venirme entonces a la cabeza el hecho de que en España gritamos mucho más que casi cualquier otro país al hablar, lo que debería influir de manera muy negativa en la expansión de esta pandemia. ¿Quizás que hablemos más alto que otros y tendamos a tocarnos mucho más podría explicar porqué la pandemia se extiende más en España que en otros países del entorno, como Portugal?

El artículo se publicó en la revista Scientific Reports, en el volumen 9: Scientific Reports, 9, 2348

(1) La ruptura de película fluida es el fenómeno que se produce cuando en una superficie hay un líquido rodeándola y pasa un gas rápidamente. El paso del gas causa deformaciones en la película del líquido que terminan por «romperlo» y extraer gotas de líquido que serán arrastradas por el gas.

(2) Estos cuatro idiomas no sólo cuentan con un porcentaje de hablantes muy representativo del total de la población humana, sino que además poseen tales diferencias sintácticas y de pronunciación que al usarlos como ejemplos permiten generar datos útiles para todas las hablas humanas.

(3) La media cuadrática es la raíz cuadrada de la suma de los cuadrados de unos valores, divididos por el número de valores. En la wikipedia en español lo explican muy bien: Wiki:Media Cuadrática

Los metales también son fluidos, aunque algo raritos.

Cuando les explico a mis alumnos el concepto de medio continuo, siempre trato de que se den cuenta de que los fluidos no sólo son los líquidos y gases a los que estamos acostumbrados, que otros elementos pueden ser fluidos bajo circunstancias favorables. Por ejemplo, el metal mercurio fluye a temperatura y presión habituales. Y hay aleaciones de metales que calentados con el calor de la mano, empiezan a fluir porque su temperatura de fusión es muy baja, por debajo de la corporal, como por ejemplo el galio(1). Además, determinadas aleaciones que tienen una gran utilidad industrial, o que pueden tenerla en el futuro, son líquidas a temperaturas no tan altas.

Una de estas aleaciones es la de plomo con litio, que es líquida a temperaturas del orden de los cientos de grados y que se pretende usar para recoger la energía de los futuros reactores de fusión. La idea es que esta aleación se caliente un montón en el núcleo del reactor y que después intercambie parte de ese calor con un intercambiador externo, que moverá una turbina para producir energía eléctrica.

Para poder hacer todo esto, además de estudiar la forma de lograr fusión con generación positiva de energía, hay que tener claro cómo se mueve el fluido formado por la aleación de plomo y litio. Pero hay un problema: al ser dos metales, son muy sensibles a los campos eléctricos y magnéticos, de forma que las ecuaciones y números adimensionales habituales en la mecánica de fluidos no son suficientes, hay que usar lo que se denomina magneto-hidrodinámica. Es decir, la unión de las ecuaciones que gobiernan el movimiento de los fluidos con las que presentan el movimiento de las cargas eléctricas. Y eso es lo que hicieron, al menos en parte, en un estudio muy interesante en el que hicieron fluir esta aleación por una tubería de acero calentada por debajo.

Comienzan el artículo diciendo que los metales líquidos se han propuesto como enfriadores y generadores de helio, esto último el litio(2). Se pretende emplear estas aleaciones por su alta capacidad térmica, que pueden absorber mucho calor de la reacción de fusión, y su alto punto de ebullición, que necesitan temperaturas muy altas para ponerse a hervir, es decir, a transformarse en gas metálico. Al ser metales, como ya comenté antes, tienen que tenerse en cuenta los efectos de las cargas eléctricas y los campos magnéticos, y de hecho varios estudios, según los autores del artículo, lo han hecho así. Por otra parte, los movimientos de transporte de calor mediante fluidos(3) para estos metales bajo la acción de un campo magnético son importántisimos en la metalurgia y el crecimiento de cristales. No deberíamos olvidar que los metales son cristales, y que sus propiedades dependen en gran manera de qué tipo de cristal forma al enfriarse el metal, que a su vez depende de manera muy fuerte de los flujos de la fase líquida del metal, con lo que la investigación de estos autores tiene muchos usos, amén del simple placer de saber más sobre un sistema tan interesante como son los líquidos con propiedades eléctricas.

La introducción sigue comentando que una gran cantidad de estudios numéricos se han hecho para poder definir varios parámetros de la dinámica de estos líquidos, junto con varios estudios experimentales, especialmente con líquidos que se parecen mucho a los metales, pero que no lo son.

Continúan después explicando las fuerzas principales que actúan sobre la convección en un líquido que responde a campos magnéticos: la fuerzas electromagnéticas, la de flotación(4) y las de inercia, o movimiento, cuando el fluido posee viscosidad.

Las fuerzas electromagnéticas por un lado, aumentan la disipación de parte de la energía cinética del fluido debido al rozamiento forzado por los campos magnéticos, lo que reduce su inestabilidad, y por otro genera estructuras que provocan sus propios tipos de inestabilidades.

Las fuerzas de flotación hacen que el fluido se «organice» en columnas para conectar las regiones más calientes y las más frías, mientras que las fuerzas de inercia facilitan el movimiento del fluido a lo largo del flujo.

Los investigadores trataron de observar el efecto de cada una de estas fuerzas independientemente en la dinámica del fluido, para lo que usaron una instalación experimental interesante.

Sistema experimental empleado. Se observan las termocuplas empleadas para medir la temperatura de las termocuplas, los calentadores del fluido y el aislamiento para poder tener el metal a una temperatura más o menos constante. De la figura 1 del artículo citado.

Para poder tener datos de tanto la temperatura como el campo eléctrico, las termocuplas (distribuyeron 123 en todo el experimento) se usaban de doble forma: la punta de la misma proporcionaba información sobre la temperatura del fluido, mientras que el aislamiento que la rodeaba se empleaba para medir el potencial eléctrico al que estaba sometido. Además, usaron medidores de flujo y como se muestra en la figura superior, tenían platos calentadores capaces de proporcionar una gran cantidad de energía calorífica al fluido. Posteriormente, los autores del artículo dedican una cierta cantidad de espacio a explicar cómo realizaron los experimentos que no reseño, centrándome más en los resultados principales. Para poder estudiar una gran cantidad de valores, variaron los parámetros de velocidad, campo magnético y flujo de calor según la tabla siguiente:

Parámetro Valores
Velocidad(cm/s) 1, 2, 3, 4, 5, 10, 15, 20
Campo magnético (T) 0; 0,5; 1; 1,5
Flujo de calor (W/cm²) 0, 2, 4, 6

Uno de los resultados experimentales que observan, y que les permite confirmar que su sistema de medidas es adecuado, es que al aumentar la velocidad del fluido y cambiando el campo magnético aplicado, aumenta la desigualdad en la distribución de temperaturas a la salida del conducto. Cuando este campo se hace cero, apenas hay cambios en la distribución de temperaturas del fluido, aparte de una disminución de las diferencias entre las temperaturas de entrada y salida del conducto al aumentar la velocidad del fluido.

Para poder extender sus resultados y aplicarlos a situaciones muy distintas de las estudiadas experimentalmente, emplearon números adimensionales. Como querían estudiar el efectos de tres fuerzas, usaron los tres números siguientes:

Donde Ha es el número de Hartmann, Re el de Reynolds y Gr el de Grashof. Thw es la media de la temperatura de la pared, T0 la del fluido.

Ha² proporciona la relación entre las fuerzas electromagnéticas y viscosas, o de rozamiento, el de Reynolds relaciona las fuerzas de inercia o movimiento con las viscosas y el de Grashof si la fuerza de flotación domina a la de rozamiento o viscosa. Además, para poder cuantificar el efecto de la convección, se precisa el número de Richardson, definido como Gr/Re², y que proporciona la relación entre las fuerzas de flotación y las viscosas. Lo que pudieron observar es que hay tres regímenes de movimiento, cada uno dominado por una de las fuerzas.

Así, en el régimen donde la fuerza de flotabilidad domina el movimiento del fluido, precisamente por ser la fuerza dominante la de flotabilidad, se forman células convectivas que se alteran con la presencia del campo magnético y en función de la velocidad, pero siempre son los elementos dominantes del movimiento del fluido.

Cuando el campo magnético es lo suficientemente alto, más de 0,5 Tesla en este experimento, entonces el fluido está dominado por la fuerza electromagnética, lo que hace que es fluido la temperatura del fluido se estratifique, con capas claras de diferentes temperaturas. en principio, este tipo de flujos son inestables a números de Reynolds suficientemente altos, pero no pudieron observarlo en sus experimentos, precisamente porque el número de Reynolds que podían obtener era muy bajo. Cuando las velocidades que empleaban para el fluido eran altas, mayores de 10 cm/s, entonces entraban en un régimen dominado por las fuerzas de inercia. En ese caso, las influencias tanto del campo magnético como de los flujos de calor eran muy bajas en el movimiento final, de tipo turbulento y con temperaturas casi uniformes a lo largo de todo el tubo, con pequeños gradientes cerca de la pared. También observaron que en este régimen de movimiento son las fuerzas de inercia las que dominan la transferencia de calor dentro del fluido. De hecho, para poder cuantificar las diferencias entre flujos y transferencias de calor en los diferentes regímenes de movimiento que observaron, usaron otro número adimensional, el número de Nusselt(5), que describe la relación entre convección y conducción para la transferencia de calor. El empleo de este número les llevó a poder hacer el siguiente gráfico:

Valores del número de Nusselt en función del de Richardson con varios números de Hartmann. Adaptado de la figura 6 del artículo citado.

En él se observa que las diferencias en el número de Richardson pueden explicar los tres tipos de regímenes vistos anteriormente. Cuando este número es muy pequeño, Ri < 0,1; entonces las fuerzas de inercia dominan el movimiento, puesto que el flujo de calor presenta una dependencia leve con el campo magnético. Si el número es muy grande, mayor de 10, entonces la presencia del campo magnético es determinante y el papel de la convección natural es mucho más importante también. Ambos fenómenos se reflejan en que los diversos valores del campo magnético apenas cambian el valor del número de Nusselt, pero su presencia o ausencia, Ha distinto o igual a cero respectivamente, sí que cambia el valor de Nu mucho. Por último, hay una gran zona intermedia, con valores del número de Richardson entre estos dos extremos donde ni la inercia ni las fuerzas de flotación dominan el régimen del fluido, pero ambas son importantes.

El artículo continúa con distintas secciones donde presenta simulaciones con ordenador que confirman sus resultados y una sección donde discute los tres regímenes de movimiento que se observaron y confirma lo que ya dijeron antes sobre la influencia de cada tipo de fuerza en su régimen correspondiente.

El artículo se publicó en la revista Physics of Fluids, volumen 32 067107 (2020).

(1) Una web dónde explican un poco la historia de este metal y sus propiedades es esta entrada: Galio, el metal que se derrite en la mano.

(2) En inglés, el término es «breeder». Lo que quieren decir es que el litio , al ser golpeado por un neutrón, se transforma en tritio (H³) el combustible del reactor de fusión. Y como en el proceso de fusión de forman una gran cantidad de neutrones, pues podría formar el mismo combustible la propia reacción de fusión.

(3) Generalmente llamados «convectivos».

(4) Las fuerzas de flotación , «buoyancy forces» en inglés, son las debidas a diferencias de temperatura dentro del fluido, que a su vez altera la densidad del mismo, lo que provoca cambios en el movimiento del fluido. Es de todos sabido que el aire caliente tiende a subir y el frío a bajar, por ejemplo.

(5) El artículo de la wikipedia es bastante aceptable sobre el tema: Número de Nusselt – Wikipedia.

Resuelto el misterio del vuelo de la semilla del diente de león.

El Diente de león es una planta que muchísima gente conoce por su amplia presencia: es una de las plantas perennes más presente en el mundo.

Uno de los elementos más hemoso de la misma es su corona llena de semillas que al soplar con suavidad se dispersan hasta distancias realmente lejanas. Según el artículo citado al final de esta entrada, si bien generalmente llegan hasta unos 2 metros, ¡a veces pueden viajar hasta 150 km!

Y una cuestión que los autores del artículo quisieron plantearse es ¿cómo lo hacen? Es decir, quisieron encontrar qué tipo de estructuras y formas de trayectorias del aire a través de la semilla colaboran en su dispersión. El tipo de semillas de los dientes de león no es tan raro en la naturaleza, y se conocen en general como semillas con vilano, que es la estructura plumosa que sostiene al resto de la estructura: el «palo» central del que cuelga la semilla.

Para poder estudiar esta estructura, tuvieron que construir un túnel de viento especial en el que poder colocar la semilla y observar las corrientes y trayectorias del aire por la forma tan especial de la semilla del diente de león.

Los resultados, además de muy bonitos visualmente, son impresionantes, porque la estructura que se observa es un vórtice separado del vilano. Y lo curioso e impresionante es que el vórtice esté separado y en una región estable. Es algo bien sabido que los objetos sólidos al moverse en un medio fluido, como el aire, generan vórtices. Pero los conocidos hasta ahora eran de dos tipos principales: o bien el vórtice se «pegaba» al sólido, o bien se separaba del mismo en la parte de atrás, para perderse en flujos turbulentos. En el caso de las semillas de diente de león, no hace ni una cosa ni la otra: está formando una estructura estable cerca del vilano, colaborando a su empuje.

La imagen siguiente muestra precisamente ese comportamiento, tanto para la propia semilla, como para un disco plano poroso, que reproduce, más o menos, ese comportamiento.

Imágenes sobre el vórtice generado por una semilla de diente de león. a) Estructura del diente de león, con la vilano(pappus, en inglés), señalado. b) Vilano. c) Uno de los pelos del vilano. d) Esquema del montaje experimental. e) y f) Vórtice que se genera en la semilla, con el viento moviéndose a 0 y 60º de orientación del mismo. g) Vórtice habitual de un disco plano. h) Vórtice del mismo tipo de disco, pero poroso.
De la figura 1 del artículo citado.

Una de las cosas que no está clara es cómo puede afectar tanto al vórtice generado un objeto tan poco sólido. Es decir, el vilano de estas semillas tiene un grado de porosidad muy grande, 0,92 +- 0,08 según el artículo, que en principio, dificulta la transformación del flujo que pasa a través del mismo.

Pero estas semillas tienen un componente importante. Como se puede observar en la figura, cada pelo tiene una estructura muy rugosa, que implica que la capa límite(1) que hace a su alrededor es muy gruesa, tanto que interacción con la de los otros pelos situados a su alrededor, formando un volumen por el que no pasa aire, incrementando notablemente el empuje de la semilla, según pudieron observar en simulaciones los autores del artículo.

De hecho, cálculos sobre el coeficiente de arrastre de la semilla indican un valor 39 +- 5 cm/s, mucho más alto del que puede tener un disco, como se muestra en la siguiente figura:

Coeficiente de arrastre de la semilla respecto del de un disco plano. La diferencia es muy fuerte a favor de las semillas, lo que facilita su dispersión.
De la figura 2 del artículo citado.

En la continuación de sus experimentos, observaron que la formación de este vórtice circular no duraba a lo largo de todos los valores del número de Reynolds(2), si no que había un valor crítico para el mismo a partir del cual se pierde el vórtice. Comprobaciones realizadas por los científicos sobre qué valores tomaba ese valor crítico en función de la porosidad se pueden resumir en la siguiente imagen, donde se observa que para valores del número de Reynolds debajo del crítico por encima del crítico, no se puede generar este vórtice:

Frontera del número de Reynolds que genera el vórtice separado, para el disco poroso(a) y un aumento de otra parte más pequeña(b).
De la figura 4 del artículo citado.

El artículo termina haciendo una revisión del mismo tipo de mecanismos para otros seres del mundo animal, especialmente pequeños insectos.

El artículo esa disponible en la dirección:

Nature volume 562, pages414–418 (2018)

(1) Capa límite: Cuando un sólido se sitúa en una corriente de fluido, se puede observar que suficientemente alejados del sólido, el flujo del fluido no se ve afectado por el sólido. La superficie alrededor del sólido donde se observan cambios en el flujo del fluido es lo que se llama «capa límite». El artículo de la Wikipedia es bastan bueno: capa límite (Wikipedia)

(2) Número de Reynolds: Una cantidad adimensional que relaciona las energías debido al rozamiento con el fluido y la debida a la velocidad. En el caso de este artículo, se escribe como UD/v, con U la velocidad del aire, D el diámetro del vilano y v la viscosidad del mismo. El artículo de la Wikipedia es bueno: número de Reynolds (Wikipedia)

Electrones como partículas fluidas. Mediciones directas

Uno de los aspectos más fascinantes de la mecánica cuántica es el hecho de que el comportamiento colectivo de las partículas se aleja mucho del esperado para cada una de ellas individualmente.

Así, se pensaba y teorizaba que los electrones en movimiento colectivo llegaría un momento en el que se comportarían como un fluido, de forma que podría tener una dinámica de flujo en régimen laminar, con un campo de velocidades de tipo Poiseuille. La forma en la que esto pasa es análoga a la aproximación de medio continuo que se hace de un fluido: cuando tienes un montón de partículas tan grande que el contarlas es imposible, puede decir que la distancias entre ellas se hacen cero y tienes un material continuo, aunque en realidad esté formado por partículas o moléculas discretas. En el caso de los electrones, el factor que hace que se pueda pasar de un régimen «molecular», donde cada electrón está aislado, a otro «fluido» es la temperatura del medio en el que se encuentra el electrón y la densidad de electrones presentes para actuar como portadores de corriente eléctrica, llamada densidad de portadores.

En un experimento muy reciente publicado en la revista Nature, un grupo de investigadores, usando un substrato de grafeno combinado con nitruro de boro hexagonal(1), y controlando la densidad de portadores del mismo y su temperatura, pudieron observar experimentalmente estos dos regímenes: el de Poiseuille y el «balístico» o discreto.

Concretamente, observaron en lugar de la velocidad asociada a los fluidos más habituales, el campo eléctrico, que por lo tanto depende de dos maneras distintas de la corriente transversal, como muestran en la figura 2, de la que se extrajo la siguiente gráfica:

Imagen extraída de la figura 2 del artículo. Se observa el resultado de la medida experimental del campo eléctrico producido en el material en la dos situaciones, cuando se considera el modelo «balístico» (izquierda) y el «fluido» (derecha) o de Poiseuille (izquierda), con su característica curva parabólica.

El «fluido de electrones» tiene un número de Knudsen de valor 0,16; esto sitúa al este tipo de fluido dentro del modelo de medio continuo.

En el artículo indican con claridad que sus medidas de la corriente eléctrica es muy parecida para ambos casos, pues la distribución de corriente varía muy poco con la distribución de movilidad de los electrones.

Después de observar la emergencia de la distribución de Poiseuille en los electrones, los investigadores se dedicaron a comprobar cómo afectaba a esta fase las variaciones en la densidad de portadores y la temperatura del material, T, obteniendo un diagrama de fases.

En este diagrama se emplean las distancias lMR y lee, que se corresponden con el camino libre medio de relajación del momento(2) y la longitud de dispersión electrón-electrón(3) dividida por el ancho del material, W, en el que se hacen las medidas.

Para calcular las diversas «fases» del material usaron como parámetro de medida la curvatura del campo eléctrico, dado que es un buen indicador del tipo de modelo que sigue la dinámica de los electrones.

De la figure 3 del artículo. Diagrama de fases obtenido por los investigadores. Los cuadrados insertados en las esquinas representan la distribución del campo eléctrico (línea negra con sombreado violeta) y la forma en la que se dispersan los electrones (dibujo a la izquierda). En esos diagramas, las cruces son los fonones(4) o impurezas que dispersan los electrones.

Notas:

(1) Un material en el que los electrones pueden moverse a distancias controlables desde el exterior del material.

(2) Momentum-relaxing mean free path en el artículo. Esencialemnte, la distancia que le lleva al electrón perder una gran cantidad de moemnto lineal, de energía cinḉetica por lo tanto.

(3) electron-electron scattering length en el ariculo. La distancia mínima a la que tiene que estar dos electrones para poder dispersasrse por choques entre ellos.

(4) Los fonones son la expresión del movimiento iónico debido a su temperatura.

El artículo original se encuentra aquí.

Impresión en 3D realmente rápida

La impresión en 3D es joven, tiene unos treinta años y se empieza a emplear en multitud de aplicaciones y materiales. Uno de los problemas más graves de la fabricación aditiva o impresión en 3D, estriba en la lentitud del proceso, lo que limita seriamente sus posibilidades en la industria.

Pues unos investigadores han descubierto un sistema capaz de imprimir casi cualquier producto que pueda ser endurecido, o curado, según métodos químicos u ópticos, que además, no presenta algunas de las limitaciones más habituales y exigentes en cuanto al tamaño de impresión, como que todo el volumen de impresión se alcance por el brazo «impresor», el sistema de extrusión

El sistema empleado es el uso de un gel granular como medio de suspensión. En él se introduce mediante algún brazo robótico el líquido a endurecer, se endurece según su método habitual y luego se puede extraer, lavando la pieza producida. La clave es que este gel se comporta de dos maneras distintas según la tensión que se le introduce: Si está sometido a una tensión grande, actúa como un líquido, que rodea el objeto como el agua una cuchara que se introduce en un vaso. Si, por el contrario, la fuerza ejercida por el objeto sumergido en el gel es pequeña, actúa como un sólido, sujetando el material que la aguja a dejado en su interior. El gel se hace con un polímero que se usa en cosmética al que se añade agua…

Un detalle muy curioso es que el sistema de impresión no se basa en hacer rodajas finas que luego se imprimirán capa a capa, sino que más bien el objeto a imprimir se de be visualizar como una línea tridimensional que se convierte a una línea paramétrica cuasi contínua, al estilo de los sistemas CNC, donde las rutas de la herramienta son una línea.

Impresión por RLP de un cilindro de 15 x 15 x 20 cm en goma. ¡El tiempo total de la impresión fue de 4 min y 49 s! Imagen del artículo https://link.springer.com/article/10.1140%2Fepjd%2Fe2007-00305-4

El artículo está publicado en https://link.springer.com/article/10.1140%2Fepjd%2Fe2007-00305-4

Mayor comprensión de los diversos mecanismos de formación de superficies hidrofóbicas.

En un artículo reciente, unos investigadores han logrado medir con mayor precisión la tensión generada en una gota sobre tres tipos de superficies hidrofóbicas, esto es, que repelen los líquidos en su superficie, logrando confirmaciones experimentales de modelos sobre la tensión ejercida por la gota con la superficie en movimiento.

Esta medida es importante porque la tensión producida sobre la hoja «desfavorece» el movimiento. Es decir, cuanto más pequeña sea, más hidrofóbica es una superficie. Y además, saber cómo se comporta con la velocidad relativa del fluido sobre la superficie es fundamental si quieres calcular, o estimar, el rozamiento del fluido en la superficie. Y hasta ahora nadie había logrado observar las diferencias entre las diversas superficies hidrofóbicas con tanto nivel de detalle.

Figura 01. Del artículo PHYSICAL REVIEW LETTERS 120, 244503 (2018)

Como indican en el artículo, una de las claves está en el método que tienen para poder medir las fuerzas. Como cualquier idea genial, es simplísima una vez que se cuenta, pero muy difícil de darse cuenta y de hacer: Usan un «cantilever», que parece ser se traduce por guía voladiza, pegada a la gota. Es decir, una finísima barra de cristal, concretamente un tubo capilar, se acerca con cuidad extremo a la gota del líquido sobre la superficie para poder medir la flexión en el tubo de cristal, y por aplicación directa de la ley de Hooke ( F = k Δx ) sacan del desplazamiento la fuerza, fijaos en la figura 1. La otra opción genial es deslizarla  un ángulo determinado y comprobar su dinámica en el tiempo, su x(t), que es muy distinta según la gota esté sometida o no a una fuerza constante o a ninguna fuerza.

Con el segundo método se obtiene la segunda figura, donde los desplazamientos a lo largo del tiempo evidencian las fuerzas a las que se somete la gota por la superficie en la que se desliza.

Figura 02. x(t) para las tres superficies estudiadas. Del artículo PHYSICAL REVIEW LETTERS 120, 244503 (2018)

Las tres superficies hidrofóbicas estudiadas son las más comunes:

  • Una superficie conformada con pilares nanométricos para atrapar el aire y generar menos arrastre de la gota,
  • Una superficie con «cepillos moleculares», que debido a las proteínas que forman la superficie impiden el paso del líquido y
  • Una superficie lubricada con un aceite, lo que provoca un mayor deslizamiento de la gota del agua por la superficie.

Los tres tipos de superficies hidrofóbicas estudiadas en el artículo.
De PHYSICAL REVIEW LETTERS 120, 244503 (2018)

La figura 03 muestra un ejemplo de los tres tipos de superficies. El artículo original está aquí, y salió publicado en la revista Physical Review Letters.

Superficies hidrofóbicas que aguanten sumergidas

Uno de los mayores problemas del transporte de líquidos en general y del transporte en líquidos, es decir, del transporte marítimo, es el alto rozamiento del fluido en estado líquido. De hecho, al transportar líquido por una tubería existe el problema de que una parte importante de la energía que se le proporciona al fluido se tiene que emplear en eliminar el rozamiento del líquido con la tubería que lo transporta.

En ambos casos una solución muy elegante consiste en colocar un fluido en estado gas entre el líquido que se mueve y la superficie sólida contra la que se mueve. Entonces, el rozamiento desciende muchísimo porque lo que roza es el sólido contra un gas y un gas contra un líquido. El problema es «sujetar» el gas cerca del sólido. El muy desgraciado del gas tiene a escaparse hacia el líquido, promoviendo de nuevo ese contacto líquido-sólido que sería deseable evitar.

Una forma de mantener el gas cerca de la superficie sólida es el uso de cavidades de tamaño nanométrico, donde en principio el gas se queda algo más de tiempo. El problema es que al moverse el líquido respecto a la superficie, y simplemente por la presión del líquido, se acaba llenando de líquido la nanocavidad con gas. Hasta ahora, si ahora es el 2014, claro. En el artículo PRL-vol113-136103(2014) se presenta un modelo capaz de predecir si el aire (gas empleado) se quedará atrapado en la ranura empleada o no. Y se demuestra que el modelo es válido con una ranura real.

Según el modelo que se presenta en el artículo, la clave para lograr que una ranura «atrape» aire por un tiempo indefinido (más de 50 días en el experimento) es la altura que el agua, o líquido, tiene sobre la ranura, de forma que hay un altura crítica a partir de la cual se moja la ranura.  Las buenas noticias son que esa altura crítica depende de la anchura de la ranura, las malas que la altura crítica máxima es del orden de los centímetros, lo que dado que un barco se sumerge metros, implica que el uso de estos sistemas para evitar rozamiento queda descartado.

Sin embargo, es un gran experimento que creo interesante reseñar porque presenta datos y modelos sencillos y elegantes para entender un problema muy complejo. La esencia de la física bien hecha. El montaje experimental es el de la figura siguiente:

Montaje experimental. Artículo PRL-Vol311-136103(2014)

La figura de la izquierda muestra una ranura con las dimensiones y convenciones empleadas en el artículo, mientras que en la derecha se observa un esquema del sistema experimental. Con este montaje experimental, observar si la ranura se moja o no es cuestión de explorar imágenes proporcionadas por una cámara ajustada a la lente de la figura anterior, con lo que se obtienen gráficas como la siguiente, donde se muestra lo que pasa con altura de líquido por debajo de la crítica, es decir, con el aire atrapado de manera estable y con una altura por encima de ese valor, lo que implica que el aire no permanece en la ranura:

Permanencia o no del aire en la ranura. Artículo PRL-Vol311-136103(2014)

La forma de medir si hay aire o no es mediante la posición del menisco que se forma en la ranura. La gráfica presenta la distancia máxima de ese menisco desde el comienzo de la ranura hasta su fondo. Cuando llega a unos 80 micras, llega al fondo de la ranura. Fíjense que cuando al altura del agua es superior a la crítica, la ranura se moja, esto es, se vacía de aire en «sólo» ocho horas, mientras que para una altura de agua por debajo de la crítica, la ranura permanece indefinidamente llena de aire. Observen además la fantástica coincidencia entre el modelo y los datos experimentales, que indica que el modelo acierta en sus predicciones.

Para hacer montañas de granos, es importante saber cómo se formó la montaña.

A lo mejor no parece importante, pero un auténtico misterio de la física hasta hace poco era la formación de montones con material granular en caída libre. Es decir, yo dejo caer desde una distancia fija algo en forma granular, y trato de predecir o modelar la forma que tendrá ese montón.  Hasta hace algún tiempo había resultados experimentales y teóricos contradictorios, entre otras cosas porque no hay un modelo claro de material granular: El material granular son pequeñas piezas con formas distintas entre sí y no se sabe muy bien cómo modelar ni la forma del grano, ni la interacción entre ellos.

Piensen que el material en forma granular tiene interacciones entre granos o partículas vecinas que los separa del sólido rígido, que es el equivalente a granos formando un auténtico continuo, como en los metales, y del modelo de partículas rígidas separadas, cuando no hay demasiados granos. Un modelo que daba algún resultado decente es adaptar el modelo de sólido deformable y quizás elástico con propiedades constitutivas propias para el material granular. Es decir, se hace una aproximación de un material en estado discreto por un continuo cuya descripción encaja en los experimentos con diversos materiales granulares.

Este tipo de aproximaciones no ha sido capaz de resolver un problema de la generación de montones: que la distribución de presiones en el centro del montón depende de cómo se haya formado el montón, de forma que si se genera desde un sólo punto de caída del material, aparece una depresión en la base del montón; cuando se genera median una «lluvia», es decir desde múltiples puntos de caída del material, la depresión en el centro no es visible. En el artículo PRL – Vol113 – 068001 (2014) se demuestra que el uso de modelos elastoplásticos que no eran capaces de predecir estos dos resultados sí que funcionan, pero si se usa un modelo matemático que tiene en cuenta la historia del fenómeno para la descripción numérica.

Cuando se simula un sistema tridimensional en un ordenador, hay que hacer una malla tridimensional de puntos en la que se calculan las propiedades del material, presión, densidad, fuerzas, etc. Esta malla puede seguir o no al material en su movimiento. Cuando la malla es fija y el material se mueve dentro de ella, podemos tener en cuanta la historia de este movimiento mejor.

El resultado final es que en simulaciones con dos modelos distintos de materiales elastoplásticos, se observa la caída de presión en le centro de la pila o montón que ya fue observada experimentalmente, como la figura tres del artículo muestra:

Perfiles de presión de pilas de material granular. Del artículo PRL-Vol311-0068001 (2014), figura 3.

En la figura se muestran los perfiles de presión según el material granular caiga en forma de «lluvia», izquierda, o desde un punto, derecha. Ambos están marcados por la relación entre el ancho de la boca y el radio del montón. En el primer caso, R/W0 es 1. Cuando R/Wo es 10, es decir, todo el material cae desde un sólo punto, se puede observar como según el instante de tiempo en el que observemos el perfil de presiones, éste cambia y termina desarrollando la depresión central al final.