Abstract

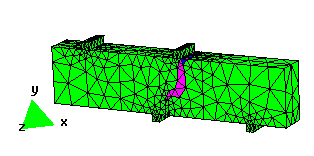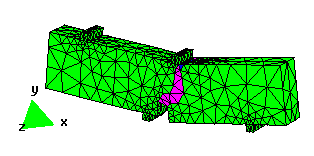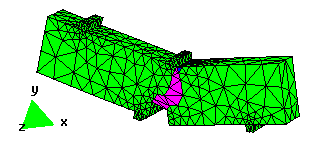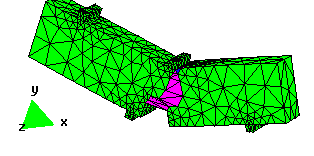
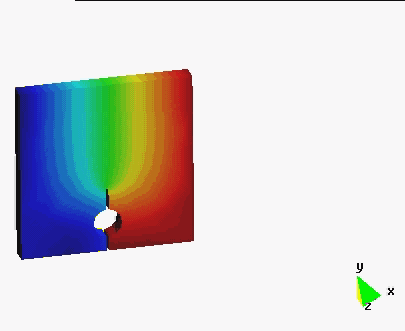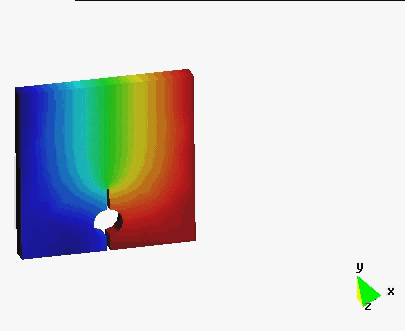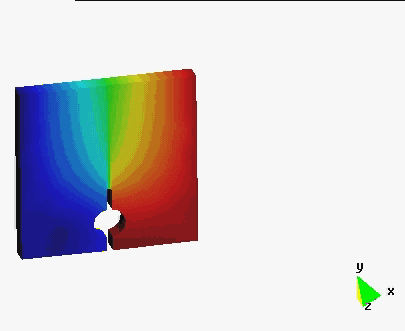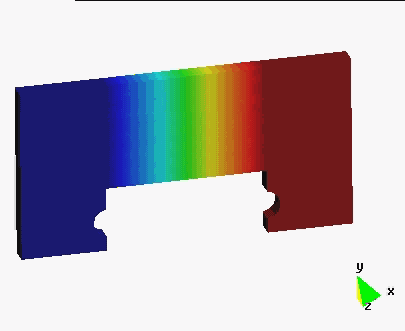
Examples

This work deals with the simulation of strain localization phenomena through the Strong Discontinuity Approach (SDA) for three dimensional (3D) problems. The main assumptions of this work are the isothermal quasi-static regime, small deformations and rotations, and a material described as homogeneous and isotropic.

The theory is developed in the ambit of Continuum Mechanics using an Isotropic Continuum Damage model and its variations, which serves to simulate materials like concrete, ceramics, rocks and ice, for example. The basic ingredients of a 3D finite element formulation with an embedded discontinuity are presented. Also the ingredients for the transition from a weak discontinuity to a strong discontinuity (a bandwidth variable model) are presented.

An extensive analysis of material bifurcation is performed. It gives us the information necessary for the propagation of a discontinuity surface. Two proposals to track this discontinuity surface are presented.

In order to illustrate the effectiveness of the method, several numerical simulations are presented. The agreement with experimental data is also shown. In this work new possibilities are open by giving the necessary tools for the extension of the method to the study of more complex examples which require more complex constitutive models.