Anuncios

Anuncios: (ver Moodle)

Organización

Clases: Miércoles, 16:00 – 19:30h

Tutoría Cualquier hora.

Referencia

Notas de Clase (Ver Sección Apuntes)

Libros de Elementos Finitos & Mecánica del Medio Continuo

BATHE, K.-J. (1996). Finite Element Procedures. Prentice-Hall, Inc., Englewood Cliffs, New Jersey, USA.

COOK, R. D. , MALKUS, D. S. & PLESHA, M.E. (1989). Concepts and Applications of Finite Element Analysis. John Wiley & Sons, Inc.

CRISFIELD, M.A. (1997). Non-Linear Finite Element Analysis of Solids and Structures, volume 1,2. John Wiley and Sons, New York, USA.

HUGHES, T.J.R. (1987). The Finite Element Method. Prentice may, Englewood Cliffs, NJ.

MALVERN, L.E. (1969). Introduction to the mechanics of a continuous medium. Prentice-Hall, Inc. New Jersey.

MASE, G.E. (1977). Mecánica del Medio Continuum. McGraw-Hill, USA.

ODEN, J.T.; BELYTSCHKO, T.; BABUSKA, I. & HUGHES, T.J.R. (2003). Research directions in computational mechanics. Computer methods in applied mechanics and enginering, Vol. 192 pag.913-922, Elsevier.

OLIVER, J. & AGELET de SARACÍBAR, C. (2000). Mecánica de medios continuos para ingenieros. Ediciones UPC, Barcelona, España.

OÑATE, E. (1992). Cálculo de Estructuras por el Método de Elementos Finitos. Centro Internacional de Métodos Numéricos en Ingeniería, Barcelona, España.

OWEN, D.R.J. & HINTON, E. (1980). Finite Elements in Plasticity: Theory and Practice. Pineridge Press Limited UK.

OWEN, D.R.J. & HINTON, E. (1984). Finite Element Software for Plates and Shells. Pineridge Press Limited UK.

RAO, S.S. (1989). The Finite Element Method in Engineering. Pergamon Press, UK.

SIMO, J. & HUGHES, T.J.R. (1998). Computational Inelasticity. Spriner-Verlag, New York.

ZIENKIEWICS, O.C. & TAYLOR, R.L. (1994a). El método de los elementos finitos. Volumen 1: Formulación básica y problemas lineales. CIMNE, Barcelona, 4ª edition.

ZIENKIEWICS, O.C. & TAYLOR, R.L. (1994b). El método de los elementos finitos. Volumen 2: Mecánica de sólidos y fluidos. Dinámica y no linealidad. CIMNE, Barcelona, 4ª edition.

Evaluación

La evaluación será continuada y flexible, mediante aplicaciones prácticas que serán desarrolladas en clase, valorando la dedicación del alumno y su actitud.

La evaluación  se completará con la entrega de un trabajo final del grupo (constituido por 3 personas como máximo) y su defensa en público.

Ejercicio y Practicas

Subroutinas en MATLAB (Actualización: 11/03/2010)

Subroutinas en FORTRAN (Actualización: 11/03/2010)

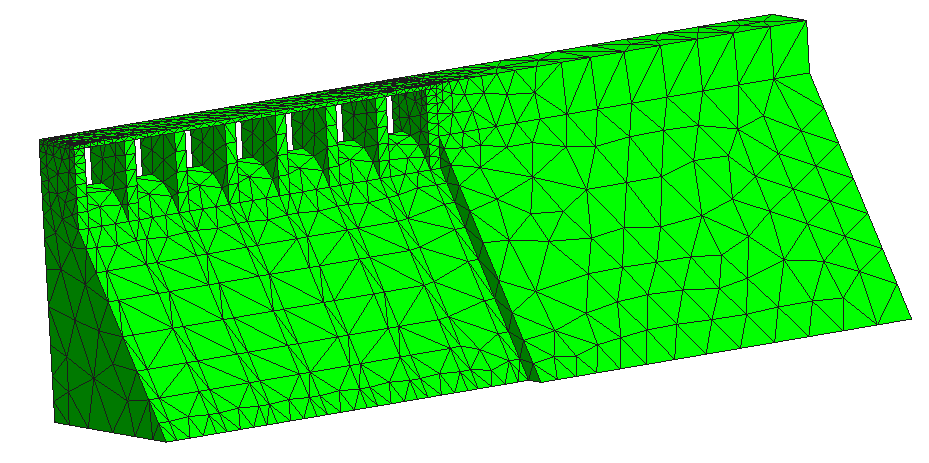
Presa en Arco (Escalere -Italia)

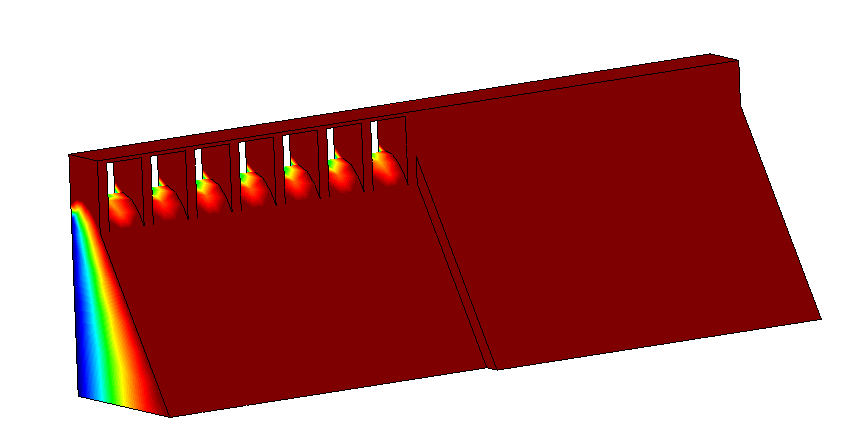
Cálculo de las tensiones, desplazamientos debido a la presión hidrostática

Cálculo de la distribución de temperatura

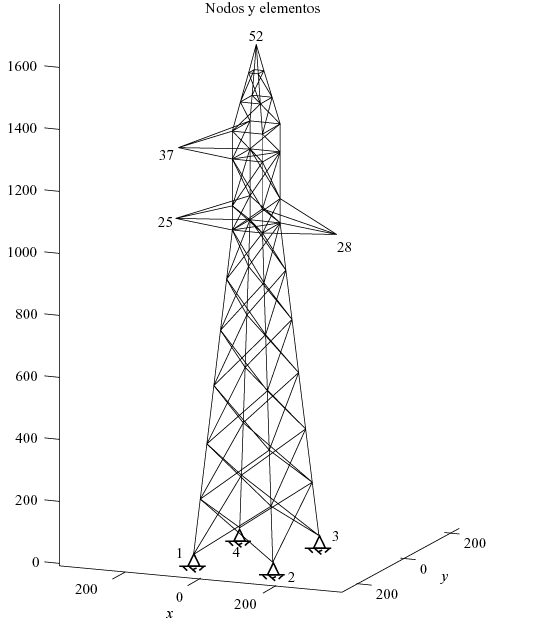
Cálculo de las tensión en una torre de alta tensión

Apuntes

CHAVES, E.W.V. & MÍNGUEZ, R. (2009). » Mecánica Computacional en la Ingeniería con Aplicaciones en MATLAB «. Editorial UCLM , ISBN:978-84-692-8273-1. (in Spanish).

Subroutinas en MATLAB (Actualización: 11/03/2010)

Subroutinas en FORTRAN (Actualización: 11/03/2010)

INTRODUCCIÓN

La Mecánica es la ciencia aplicada que estudia el comportamiento de fluidos, sólidos y materiales complejos bajo la acción de fuerzas. La Mecánica Computacional es la sub-disciplina de la Mecánica que, utilizando herramientas y métodos computacionales, estudia problemas gobernados por los principios de la Mecánica, Oden et al.(2003).

El Método de los Elementos Finitos (MEF) es una de las herramientas más poderosa de la mecánica computacional. Problemas tales como la simulación de tejido humano, simulación de trenes de alta velocidad, colisión de vehículos, proceso de embutición de chapas, proceso de excavación de túneles, y obtención de esfuerzos en estructuras, son algunos ejemplos que frecuentemente necesitan de la técnica de los Elementos Finitos (EF) para una adecuada solución.

OBJETIVOS DOCENTES

Conocimiento del Método de los Elementos Finitos para resolver problemas basados en ecuaciones en derivadas parciales dentro del contexto de la mecánica de los medios continuos, con dos finalidades primordiales: 1) que el alumno consiga la capacidad crítica suficiente para utilizar cualquier programa comercial basado en la técnica de los elementos finitos; y 2) habilitar al alumno de técnicas de programación para resolver diferentes problemas ingenieriles mediante el MEF.

CONTENIDO DE LA ASIGNATURA

Introducción 

Introducción a la mecánica computacional; Introducción al MEF; Aspectos históricos; Descripción general del método.

 Revisión de Análisis Matricial y Técnicas de Integración 

Notación matricial; Revisión de álgebra; Técnicas de resolución de sistemas de ecuaciones lineales; y métodos de integración (fórmulas de cuadratura). Implementación de los distintos métodos en MATLAB.

Técnicas de Interpolación. Funciones de Forma

Polinomio interpolador de Lagrange. Funciones de forma: elementos unidimensionales, bidimensionales, y tridimensionales.

 Elementos Finitos Unidimensional (Tipo Barra)  

Concepto básico de discretización; Matriz de rigidez; Ensamblaje de la matriz de rigidez; Implementación de un código de EF en MATLAB para problemas bi y tridimensionales; Práctica – Celosía espacial (torre de alta tensión).

 Mecánica de Sólidos. Problemas Elástico-Lineales

Revisión de la teoría de la Elasticidad Lineal; Programación de un código en MEF para problemas de Estado de Deformación Plana y de Tensión Plana; Práctica – Sensibilidad de la malla de una viga de gran canto utilizando varios elementos y distintas densidades de mallado.

Programación de un código en MEF para problemas tridimensionales; Práctica – Presa en arco.

 Solución de Forjados utilizando el MEF 

Revisión de Teoría de Placas a flexión; Revisión del problema de flexión de Vigas; Implementación del código en EF (Placas-Vigas); Práctica – Resolución e interpretación de resultados para forjados.

 Problemas de Campo. Ecuaciones de Poisson y de Laplace 

Aplicación del MEF para la resolución de problemas de campo gobernados por las ecuaciones de Laplace y Poisson: Transmisión de calor; Torsión; Flujo subterráneo. Implementación de un código de Elementos Finitos en 2-D y 3-D para su resolución.

Conocimiento extensivo del Método de los Elementos Finitos con dos finalidades primordiales: 1) que el alumno obtenga la capacidad crítica suficiente para utilizar cualquier programa comercial basado en la técnica de los Elementos Finitos; 2) habilitar al alumno de técnicas de programación para resolver diferentes problemas ingenieriles mediante el MEF.

FORMA DOCENTE

Teórica (20 horas)

Se desarrollarán clases teóricas exponiendo los conocimientos básicos necesarios para el desarrollo de las clases prácticas.

Práctica (40 horas)

Implementación de un código de elementos finitos para realizar la simulación numérica de un problema de ingeniería. El lenguaje de programación para la elaboración del código de EF podrá ser MATLAB o FORTRAN.

EVALUACIÓN

La evaluación será continuada y flexible, mediante aplicaciones prácticas que serán desarrolladas en clase, valorando la dedicación del alumno y su actitud. La evaluación se completará con la entrega de trabajos a lo largo del curso y su defensa en público.