Ejercicio 2. (3,5 puntos)
Se pretende transvasar 63 m3/h de un líquido desde el depósito D2 al D1, mediante la instalación mostrada en la figura, formada por tuberías de acero laminado nuevo, produciendo electricidad mediante las turbinas T1, T2 y T3. Datos: La válvula V1 es de compuerta, y está totalmente abierta, la válvula V2 también es de compuerta pero está abierta ¼ (considerar el menor valor de K posible). Todos los codos son redondeados a 90º. No se desprecian las pérdidas de carga a la salida y a la entrada de los depósitos. Los tanques son suficientemente grandes como para considerar sus niveles constantes.
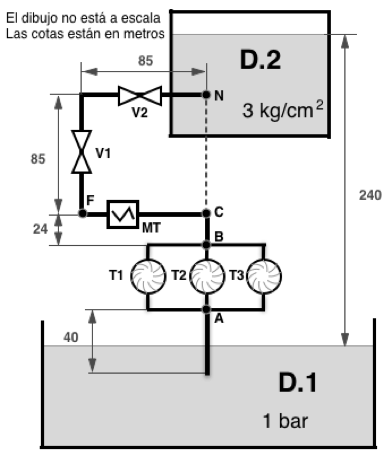
El combustible tiene una viscosidad de 7 centipoises y una densidad relativa de 1,1. Para el caudal a transvasar, las turbinas producen una pérdida de carga total de carga de 3 m. Existe un medidor de caudal (MT) tipo tobera en el tramo B-F cuyo diámetro interior es 41 mm. Supóngase el tramo AB como una longitud equivalente de 10 metros con un diámetro interior de 69 mm y 1,5 de espesor. D1 está a 1 bar.
- ¿Altura suministran las turbinas?, ¿Qué potencia proporciona cada turbina si tienen un rendimiento del 100%? (1,25 pto).
- Calcúlese el golpe de ariete en el punto A (T=0,5s), suponiendo kacero=0,45. Es necesario tener en cuenta la pérdida de carga que produce la salida, la entrada de depósito, el medidor de caudal y el resto de accesorios (1,5 pto). No tener en cuenta las turbinas.
- ¿Cuál sería el diámetro de una tubería equivalente recta desde N hasta C (dibujada de forma discontinua, sin ningún accesorio) que sustituya al tramo N-C actual? (0,75 pto).
Datos de las tuberías
| Tubería | D exterior | e |
| Tramo 1 (D1-A) | 72 mm | 1,5 mm |
| Tramo 2 (B-F) | 73 mm | 2 mm |
| Tramo 3 (F-N) | 80 mm | 2 mm |
¿Cómo se resuelve?
Cambio de algunas unidades
p2 = 3 kg/cm2 *100000 Pa / 1,033 kg/cm2 = 290416,26 Pa
p1 = 1 bar = 100000 Pa
–
Apartado 1. Para calcular la altura de las turbinas (Hturbinas), aplicamos la Ecuación de Bernoulli (E.1) al sistema.
V22/(2g) + p2/(ρg) +z 2 = V12/(2g) + p1/(ρg) + z1 + Hr + Hturbinas (E.1)
–
Como los tanques son lo suficientemente grandes como para considerar sus niveles constantes, los términos de velocidad de la ecuación, V22/(2g) y V12/(2g), será similares y se anularan uno al otro. Los términos de presión (p2/(ρg) y p1/(ρg)) y altura(z2 y z1) son conocidos y el término de pérdida de carga (Hr) habrá que calcularlo.
Para calcular Hr se utiliza la ecuación de Darcy-Weisbach (E.2)
Hr= (fL/D+∑K)*V2/(2g) (E.2)
Donde:
f: coeficiente de fricción
L: longitud de la tubería
D: Diámetro de la tubería
ΣK: coeficiente de pérdida de los accesorios
V: velocidad en la tubería
El coeficiente de fricción (f) se calcula con la fórmula de Colebrook (E.3)
1/√f=-2log(k/(3,7D+2,51/(Re√f0)) (E.3)
Pero para completar esta fórmula se necesita:
- Rugosidad relativa k/D
- Nº de Reynolds (Re), Re = 4 Q /(π D υ) (E.4), para el cual necesitamos la viscosidad cinemática, que se calcula usando la ecuación υ = μ / ρ (E.5)
Con estos dos datos se consulta el Diagrama de Moody para obtener una primera f0 para comenzar a iterar, hasta que la diferencia absoluta entre dos f consecutivas sea menor o igual a 0,0001.
La velocidad (V) se calcula con la ecuación con la Ecuación de Continuidad (E.6)
V = 4 Q / (π D2) (E.6)
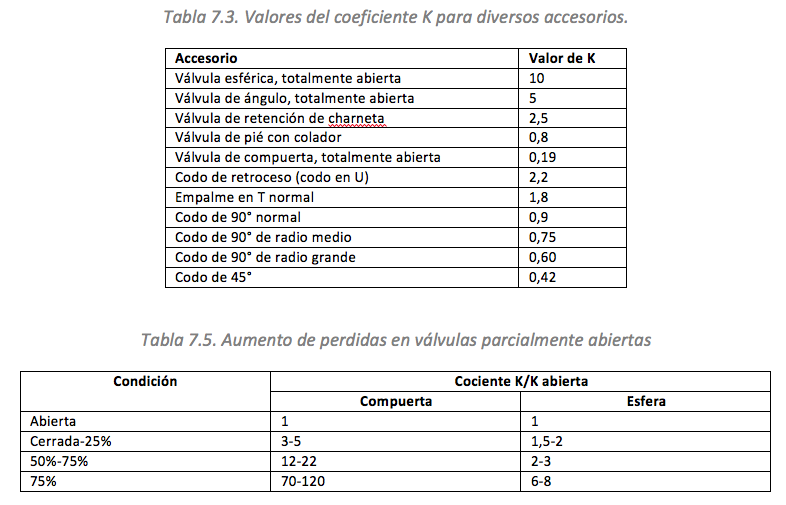
La sumatoria de los coeficientes de pérdida (ΣK), se calcula según los accesorios que haya en tramo a calcular con la ayuda de las Tablas 7.3 y 7.5 del formulario (Agüera, J. «Mecánica de Fluidos» 2002). Teniendo en cuenta que, adicionalmente, el coeficiente de pérdida por salida de depósito es KSD = 0,42 y el de entrada a depósito KED = 1
La pérdida de carga se calcula por tramos con el mismo diámetro. Los diámetros interiores de los tramos y las longitudes se presentan en la Tabla 1. En este caso habrá 2 tramos: Tramo de F-D1 y Tramo 3 de F-N.
Tabla 1. Longitudes y diámetros
| Tubería | D interior | Longitud |
| Tramo D1-A | 69 mm | 40 m |
| Tramo B-F | 69 mm | 109 m |
| Tramo 3 (F-N) | 76 mm | 170 m |
Para calcular la viscosidad cinemática es necesario cambiar las unidades de la viscosidad absoluta (μ) y la densidad (ρ). (1 centipoises = 0,001 kg/ms )
υ = μ / ρ=0,007 kg/ms / 1100 kg/m3 = 6,36*10-6 m2/s
Cálculo de Hr para el tramo F-D1 (Tramo 1).
Hr1= (f1L1/D1+∑K1)*V12/(2g) (E.2)
El coeficiente de fricción (f1) se calcula con la fórmula de Colebrook (E.3)
1/√f=-2log(k/(3,7D+2,51/(Re√f0)) (E.3)
En este caso:
Rugosidad relativa k/D, en este caso k/D = 0,05 mm / 69 mm = 0,0007246
Nº de Reynolds (Re) Re = 4 Q /(π D υ) = 50744,93
Con el diagrama de Moody la f0 será 0,023 (Obtenido de Figura 1)
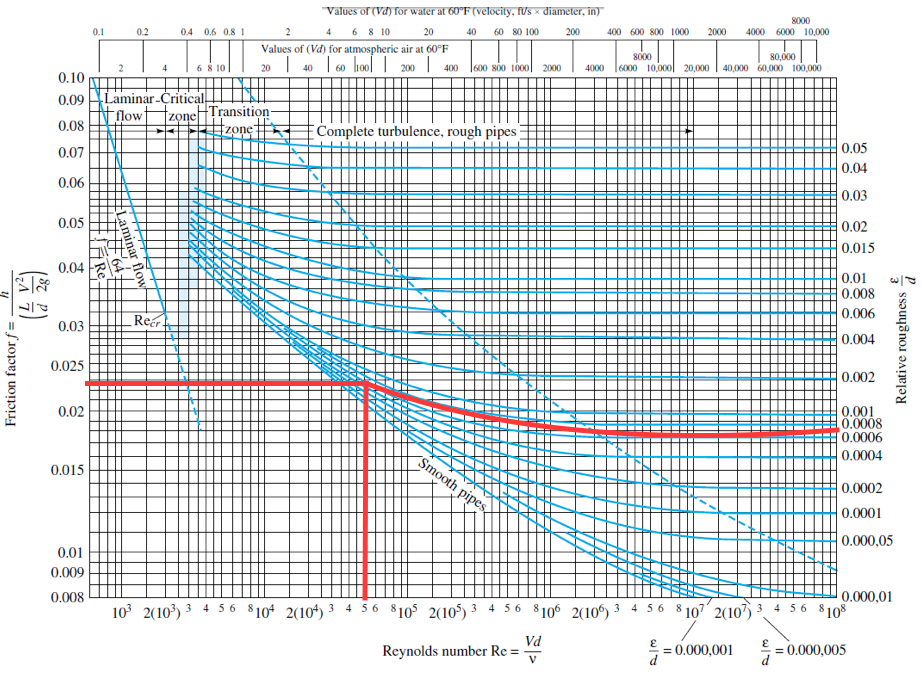
Figura 1. Diagrama de Moody
Primera Iteración con E.3 f1er_iteración = 0,02320.
Como ΙΙ f0 – f1er_iteración ΙΙ = 0,0002 > 0,0001, y por tanto, hay que iterar de nuevo.
Segunda iteración con E.3 (ahora f0 en la fórmula es 0,02320) f2º_iteración = 0,02318.
Ahora ΙΙ f1er_iteración – f2º_iteración ΙΙ = 0,00001 < 0,0001, por tanto usaremos f = 0,02318
La longitud (L1) L1= LD1-A+LA-B+LB-F = 40 m + 10 m + 109 m = 159 m
La velocidad (V1) V1= 4 Q / (π D12) = 4,68 m/s
Las pérdidas locales en ese tramo son la salida de depósito y dos codos, por tanto
ΣK1 = KSD + Kcodo= 0,42 + 2*0,9 = 2,22
La pérdida de carga resultante es: Hr1= (f1L1/D1+∑K1)*V12/(2g) = 62,19 m
En este tramo hay un medidor de caudal, cuya pérdida de carga debe ser calculada separadamente, con la fórmula E.7. y la Figura 8.5 del Formulario para calcular la K (Figura 2).
HrMT=K*VMT2/(2g) (E.7)
Figura 2. Coeficientes de pérdida para los medidores de caudal
En este caso la pérdida de carga que produce este medidor es HrMT = 4,48 m
Cálculo de Hr para el tramo F-N (Tramo 3).
Hr3= (f3L3/D3+∑K3)*V32/(2g) (E.2)
El coeficiente de fricción (f3) se calcula igual que el anterior.
En este caso:
- Rugosidad relativa k/D, en este caso k/D = 0,05 mm / 76 mm = 0,0006579
- Nº de Reynolds (Re) Re = 4 Q /(π D υ) = 46071,06
Con el diagrama de Moody la f0 será 0,024
Primera Iteración f1er_iteración = 0,02329.
Como ΙΙ f0 – f1er_iteración ΙΙ = 0,0007 > 0,0001, y por tanto, hay que iterar de nuevo.
Segunda iteración (ahora f0 en la fórmula es 0,02329) f2º_iteración = 0,02335.
Ahora ΙΙ f1er_iteración – f2º_iteración ΙΙ = 0,00006 < 0,0001, por tanto usaremos ésta última f = 0,02335
La longitud (L3) L3= LN-F = 170 m
La velocidad (V3) V3= 4 Q / (π D32) = 3,85 m/s
Las pérdidas locales en ese tramo son la entrada de depósito, un codo, una válvula de compuerta abierta y otra 1/4 abierta, por tanto:
ΣK3 = KED + Kcodo+KVabierta + K1/4abierta = 1 + 0,9 + 0,19 + 70*0,19= 15,39
La pérdida de carga resultante es: Hr3= (f3L3/D3+∑K3)*V32/(2g) = 51,33 m
Despejando la Hturbinas de la fórmula de Bernoulli
Hturbinas = (p2-p1)/(ρg) +z 2 -z1 – Hr = 136,64 m
Como las tres turbinas son iguales, la altura que proporciona cada una ellas será 1/3 de la total. Por tanto, la potencia de cada una de ellas se calculará con la ecuación E.8.
P = ρ*g*Q*H/3 = 8592,88 W E.8
Apartado 2. Para calcular el golpe de ariete, se estudian los tramos por los que pasará el golpe de ariete. En este caso, el golpe de ariete se produce en A y va en sentido contrario a la corriente hasta llegar al depósito 2. Para saber el golpe de ariete, se utilizan las ecuaciones E.9 (Fórmula de Allievi) y E.10. (Fórmula de Micheaud).
ΔH = c*V/g E.9 ΔH = 2*L*V/(g*T) E.10
Donde:
ΔH: Golpe de Ariete
c: celeridad media
V: velocidad media
L: longitud total
T: tiempo de cierre de la válvula
La celeridad de la onda (aproximada, pues el combustible no es agua) se calcula con la ecuación E.11
c = 9900 / √ (48,3+k(D/e)) E.11
La celeridad de la onda (c), depende del diámetro interior y del espesor. En la Tabla 2 se muestran los diámetros, espesores y valores de la celeridad de los cuatro tramos de la instalación.
Tabla 2. Diámetros, espesores y celeridades
| Tubería | D interior | e | c |
| Tramo 1 (D1-A) | 69mm | 1,5 mm | 1191,81 m/s |
| Tramo A-B | 69 mm | 1,5 mm | 1191,81 m/s |
| Tramo 2 (B-F) | 69 mm | 2 mm | 1239,19 m/s |
| Tramo 3 (F-N) | 76 mm | 2 mm | 1224,18 m/s |
Para calcular la celeridad media (E.12) es necesario conocer la longitud equivalente de cada tramo. Para ello hay que tener en cuenta la longitud de cada tramo y la longitud equivalente que produce cada uno de los accesorios.
cm = Ltotal / Σ(Li/ci) E.12
Las longitudes equivalentes se calculan usando la Tabla 7.6 del formulario.
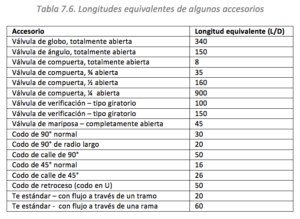
Para los accesorios que no vienen en la tabla se usa la fórmula E.13.
Le = K *D / f E.13
Para calcular la velocidad media se aplica la fórmula E.14
Vm = Σ(LiVi)/Ltotal E.14
Para saber si hay que calcular el golpe de ariete con la fórmula E.9 o con la E.10, es necesario saber la longitud crítica de la tubería (E.15)
Lc = T *cm /2 E.15
Si la longitud crítica es mayor que la longitud total, se aplicará la E.10 (Micheaud) y sino se aplicará la E.9 (Allievi).
La Tabla 3 muestra las longitudes equivalente de cada uno de los tramos
Tabla 3. Longitudes equivalentes
| Tubería | L | Accesorio | L equival. |
| Tramo D1-B | 50 m | SD | L =0,42*0,069/0,02318 |
| Total D1-B 50 m + 1,25 m =51,25 m | |||
| Tramo 2 (B-F) | 109 m | 2 codos | L=2*30*0,069 |
| MT | L=0,5*0,069/0,02318 | ||
| Total B-F 109 m + 4,14 m + 1,48 m =114,62 m | |||
| Tramo 3 (F-N) | 170 m | ED | L =1*0,076/0,02318 |
| V1 | L=8*0,076 | ||
| V2 | L=900*0,076 | ||
| 1 codo | L=30*0,076 | ||
| Total F-N 170 m + 3,27 m + 2,28 m + 0,6 m + 68,4 m =244,56 m | |||
Con la ecuación E.12
cm = (51,25m+114,62+244,56) / (51,25/1191,81 + 114,62/1239,19 + 244,56/1224,18) = 1224,17 m/s
Con la ecuación E.13 se calcula la velocidad media dando como resultado Vm = 4,18 m/s
La longitud crítica tiene un valor de 306, 04 m. Como la longitud crítica es menor que la longitud total, el golpe de ariete se calculará con la fórmula de Allievi, obteniéndose ΔH = 523,39 m
Apartado 3. Se va sustituir un tramo de tubería compuesta por:
- Un tramo de 244,56 m + 85 m + 1,48 m + 2,07 m y diámetro 0,076 m
- Un tramo de 85 m + 1,48 m + 2,07 m y diámetro 0,069 m
Por tramo recto de 85 m de longitud de diámetro ¿??
Para ello, usamos la fórmula E.15, que permite calcular un tubería equivalente a varias tuberías en serie.
Para el caso que plantea el ejercicio, como ya tenemos calculadas los longitudes equivalentes de los accesorios que se incluyen en la tubería equivalente, se puede simplificar quitando el término correspondiente a los coeficientes de pérdida. La ecuación quedaría del modo siguiente:f * Ltotal / De5 = f1 * Le_C-F / D15+f3 * Le_F-N / D35 E.15
Donde
f coeficiente de fricción de la nueva tubería, puede ser calculado (aproximadamente) como (f1 – f3) / 2
Al despejar el diámetro (De) de la ecuación E.15, se obtiene: De = 0,074 m