Ejercicio 1. (1,5 puntos)
En el depósito de la figura determinar las alturas que marcan los tubos piezométricos (h1, h2, h3) y el manómetro de mercurio (h4). A la salida de todos los manómetros hay presión atmosférica. El valor de presión señalado en el aire (-0.18 kg/cm2) corresponde a una medida de presión diferencial a 15 metros (en la SLL del líquido de densidad 700 kg/m3). Presión atmosférica: 101325 Pa. Diámetro de los manómetros despreciable.
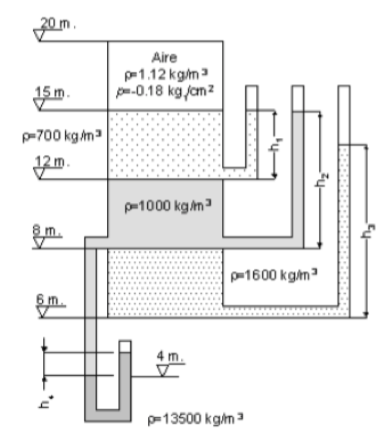
Este problema pertenece al libro de ‘Problemas de Mecánica de Fluidos con sus soluciones’ de Alejandro Rivas (2008) de la Universidad de Navarra. Escuela Superior de Ingenieros, aunque el texto del ejercicio ha variado ligeramente. ρ
¿Cómo se resuelve?
La presión a la altura de 15 m es de -0.18 kg/cm2, que en unidades SI equivale a -17655,85 Pa (1 atmósfera = 1,033 kg/cm2 ). Como este valor de presión es diferencial, hay dos caminos para solucionar el problema: 1) Utilizar presiones absolutas, sumando 101325 Pa a la presión a 15 m ; 2) Utilizar presiones diferenciales, en este caso, todas presiones deben ser diferenciales, esto implica que la presión en la SLL de los tubos piezométricos sera considerada nula.
Elegimos esta segunda opción que requiere menos cálculos.
Calculamos h1, para eso aplicamos la Ecuación de un líquido en equilibrio entre las alturas 15 m y 12 m (E.1) y después entre 12 m y la SLL del piezométrico 1 (E.2).
p15 = p12 –ρ700*g*(h15-h12) (E.1)
p12 = ρ700*g*(h1) (E.2)
Si sumamos las dos ecuaciones y despejamos h1 (E.3)
h1 =p15/(ρ700*g)+(h15-h12) (E.3)
Solución:
h1=-17655,85 Pa /(700 kg/m3*9,8 m/s2)+15 m -12 m = 0,426 m
Para calcular h2, utilizamos la ecuación E.1 y la Ecuación de un líquido en equilibrio entre las alturas 12 m y 18 m (E.4) y después entre 8m y la SLL del piezométrico 2 (E.5).
p15 = p12 –ρ700*g*(h15-h12) (E.1)
p12 = p8 –ρ1000*g*(h12-h8) (E.4)
p8 = ρ1000*g*(h2) (E.5)
Si sumamos las tres ecuaciones y despejamos h2 (E.6)
h2 =[p15+ ρ700*g*(h15-h12)+ ρ1000*g*(h12-h8)]/(ρ1000*g) (E.6)
Solución:
h2 =[-17655,85 Pa+700 kg/m3*9,8 m/s2*(15 m -12 m)+1000 kg/m3*9,8 m/s2*(12 m -8 m)]/(1000 kg/m3*9,8 m/s2) = 4,298 m
Para calcular el h4, utilizamos las ecuaciones E.1 y la Ecuación de un líquido en equilibrio entre las alturas 12 m y 4 m (E.7) y después entre 4 m y la SLL del manómetro 4 (E.8).
p15 = p12 –ρ700*g*(h15-h12) (E.1)
p12 = p4 –ρ1000*g*(h12-h4) (E.7)
p4 = ρ13500*g*(h4) (E.5)
Si sumamos las tres ecuaciones y despejamos h4 (E.8)
h4 =[p15+ ρ700*g*(h15-h12)+ ρ1000*g*(h12-h4)]/(ρ13500*g) (E.8)
Solución:
h4 =[-17655,85 Pa+700 kg/m3*9,8 m/s2*(15 m -12 m)+1000 kg/m3*9,8 m/s2*(12 m -4 m)]/(13500 kg/m3*9,8 m/s2) = 0,614 m
Finalmente, para calcular h3, utilizamos las ecuaciones E.1, E.4 y la Ecuación de un líquido en equilibrio entre las alturas 8 m y 6 m (E.9) y después entre 4 m y la SLL del manómetro 4 (E.10).
p15 = p12 –ρ700*g*(h15-h12) (E.1)
p12 = p8 –ρ1000*g*(h12-h8) (E.4)
p8 = p6 –ρ1600*g*(h8-h6) (E.9)
p6 = ρ1600*g*(h4) (E.10)
Si sumamos las tres ecuaciones y despejamos h3 (E.11)
h3 =[p15+ ρ700*g*(h15-h12)+ ρ1000*g*(h12-h8)+ρ1600*g*(h8-h6) ]/(ρ1600*g) (E.11)
Solución:
h3 =[-17655,85 Pa+700 kg/m3*9,8 m/s2*(15 m -12 m)+1000 kg/m3*9,8 m/s2*(12 m -8 m)+1600 kg/m3*9,8 m/s2*(8 m -6 m)]/(1600 kg/m3*9,8 m/s2) = 4,686 m