In this link you can find my last presentation at INFORMS 2020:
The Impact Of Undershoots On Determining The Fill-rate For A (s,S) System
The abstract of the presentation is the following:
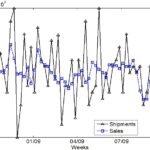
The correct sizing of the safety stock is a paramount problem that aims to achieve a compromise between customer service level and inventory investment. Typically, the safety stock can be calculated using the quantile of the future lead time demand distribution. That quantile is selected given a target Cycle Service Level. This approach suffers from different weaknesses. Firstly, on the demand side, how to forecast the lead time demand distribution. To solve that, a well-known alternative is to assume an i.i.d. gaussian distribution. However, recent data-driven/empirical approaches have overcome that approach, as Kernel Density Estimators (if the demand distribution is unknown) and GARCH models (if the variability time independence assumption is not fulfilled). Nonetheless, even when a good density forecast of the lead time demand is available, still, a second problem from the inventory perspective is present and it is the presence of undershoots. Essentially, an undershoot occurs when the inventory position does not reach exactly the reorder point, but a certain amount below it. If undershoot are not neglected, then the safety stock based on the lead time demand quantile is biased.
The correct sizing of the safety stock is a problem of paramount importance that aims to achieve a compromise between customer service level and inventory investment. Safety stock can be calculated using the quantile of the future lead time demand distribution. However, that approach ignores the presence of undershoots. In this work, we propose a non-parametric approach based on State Dependent Parameter estimates to correct that bias. This data-driven approach is illustrated using a (S-1,S) order up to level inventory policy. Simulations and real data from a manufacturing company is employed to corroborate the results.








Leave a Reply