Para calcular la eficiencia de los equipos sigo la metodología de este artículo que proporciona una eficiencia de 1 o próxima a 1 para los equipos que han realizado una temporada muy por encima de sus expectativas según las casas de apuestas, y de 0 o próximo a 0 para los equipos que hayan realizado una temporada muy por debajo de sus expectativas. La siguiente tabla muestra la eficiencia de los equipos. Asimismo, calculo los puntos esperados según las casas de apuestas y la diferencia entre puntos conseguidos y los puntos esperados. Así, una diferencia positiva significa que un equipo ha tenido un rendimiento por encima del previsto.
Equipo
Eficiencia
Puntos
Puntos esperados
Diferencia
Mirandés
1,00
75
54,6
20,4
Levante
0,97
79
64,4
14,6
Huesca
0,94
64
52,2
11,8
Oviedo
0,91
75
64,8
10,2
Elche
0,90
77
67,3
9,7
Racing de Santander
0,87
71
62,5
8,5
Albacete
0,68
58
54,9
3,1
Burgos
0,64
55
52,7
2,3
Málaga
0,64
53
50,8
2,2
Granada
0,58
65
63,8
1,2
Almería
0,49
69
69,7
-0,7
Eibar
0,47
58
59,3
-1,3
Córdoba
0,42
55
57,2
-2,2
Sporting de Gijón
0,33
56
60,1
-4,1
Cádiz
0,31
55
59,5
-4,5
Deportivo de La Coruña
0,27
53
58,4
-5,4
Eldense
0,24
45
51,0
-6,0
Castellón
0,19
53
60,7
-7,7
Zaragoza
0,14
51
60,2
-9,2
Cartagena
0,05
23
34,7
-11,7
Ferrol
0,04
30
43,3
-13,3
Tenerife
0,02
36
51,7
-15,7
Puede verse como el equipo más eficiente ha sido el Mirandés con una eficiencia de 1 (0,995). Es decir, una temporada perfecta que le ha llevado al playoff de ascenso a pesar de tener una puntuación esperada de unos 55 puntos. Al haber conseguido 75 puntos ha batido a las expectativas en más de 20 puntos lo que supone una auténtica proeza.
Los seis mejores equipos en eficiencia son Mirandés, Levante, Huesca, Oviedo, Elche y Racing de Santander. De estos seis el único que no ha quedado entre los seis primeros clasificados en La Liga 2 ha sido el Huesca pues sus puntos esperados eran bajitos. Es el Almería el único que ha conseguido quedar entre los seis primeros sin haber hecho buena campaña. El motivo de ello es que el Almería ha sido el equipo con mayor puntuación esperado.
La moraleja de esto es trivial. Hay tres formas de llegar a los puestos de ascenso o al menos de playoff. La primera sería la cara, disponer de muy buena plantilla, tener muchos puntos esperados y así haciendo una temporada regular es posible entrar entre los seis mejores como ha sucedido con el Elche o Almería. La segunda forma sería tener una plantilla media-media alta y hacer una buena campaña como han hecho el Levante, Oviedo y Racing de Santander. La tercera es apelar al milagro y partiendo de un nivel de equipo bajo-medio bajo hacer una temporada espectacular como ha hecho el Mirandés.
Ojalá mi Sporting de Gijón consiga alguna de estas tres vías en la temporada 2025-2026.
Una vez concluida La Liga es el momento de ver qué equipos han rendido bien y qué equipos no lo han hecho tan bien respecto a lo que se esperaba de ellos. Un método consiste en comparar los resultados obtenidos por los equipos con lo que esperaban de ellos las casas de apuestas. Las cuotas de apuestas se pueden convertir en probabilidades implícitas y éstas se pueden convertir en una función de densidad que muestre la probabilidad que tenía un equipo de conseguir cada una de las posibles puntuaciones. A partir de ahí se puede calcular una nota entre 0 y 1. Será más próximo a cero cuando un equipo consiga muchos menos puntos que los esperados, mientras que, será próximo a uno cuando el equipo consiga muchos más puntos que los esperados. Más detalles de esta metodología pueden encontrarse en este artículo del Journal of Sports Economics.
A continuación se presenta una tabla con los puntos conseguidos, puntos esperados según las casas de apuestas y eficiencia tanto de esta temporada recién concluida (2024-2025) como de la anterior (2023-2024). La tabla aparece ordenada por el nivel de eficiencia de la temporada actual.
Quiero hacer hincapié en los cambios en eficiencia de algunos equipos como el Girona y el Real Madrid. Ambos equipos hicieron una Liga 23-24 increíble logrando una eficiencia por encima del 0,99. Sin cambiar a los entrenadores, sin embargo, esta temporada ha sido un desastre para el Girona con 41 puntos y un 0,08 de eficiencia y normalita para el Real Madrid con 84 puntos y 0,69 de eficiencia. Esto lo que quiere decir es que los buenos entrenadores pueden tener malas temporadas. Lo que diferencia a los buenos entrenadores del resto es que son capaces de tener con frecuencia buenas temporadas. Conviene recordar que el recién nombrado entrenador del Real Madrid tuvo una campaña muy mala al frente de la Real Sociedad B en la temporada 2021-2022.
Por último, voy a hablar de la lucha por la liga. Para sorpresa de algunos los puntos esperados del Real Madrid 24-25 (80,9) son mayores que los puntos esperados de la temporada 23-24 (78,9). Sin embargo, para sorpresa de pocos los puntos esperados del FC Barcelona sí que han aumentado de 76,2 a 82,1. Sin embargo, la eficiencia del Barcelona 23-24 (0,90) fue superior a la eficiencia de la temporada actual (0,82). Si el Barcelona no luchó más por la liga 23-24 fue por la actuación brutal del Real Madrid. ¿Qué hubiese sido de este Barcelona con Xavi al frente? Pues nunca se sabrá, pero los fríos números no dicen que haya habido una mejora muy grande respecto al Barca de Xavi.
Una vez concluida la primera vuelta es buen momento para preguntarse por el rendimiento de los equipos, así como, a qué probabilidades tienen los equipos de conseguir los distintos logros: ganar la liga, clasificarse para Champions o Europa League, evitar el descenso. Lo primero requiere de un análisis de eficiencia, es decir, analizar cómo de bien o cómo de mal lo han hecho los equipos dadas las expectativas que había sobre ellos. Para lo segundo, una primera posibilidad sería lanzar una encuesta y ver qué sale, si se hiciese bien seguro que los resultados serían similares a los que les voy a mostrar que se llega a ellos a través de simular la segunda vuelta 10.000. En ambos casos se usa como materia prima las cuotas de apuestas de la primera vuelta. En concreto, se hacen dos tipos de simulaciones. Una primera que se simula toda la liga, es decir como si no se hubiese jugado ningún partido que daría las probabilidades de los equipos al inicio de liga. Y una segunda que tiene en cuenta los resultados de la primera vuelta, que nos dirá las probabilidades de los equipos al concluir la primera vuelta.
Para calcular la eficiencia de los equipos sigo la metodología de este artículo que proporciona una eficiencia de 1 o próxima a 1 para los equipos que han realizado una temporada muy por encima de sus expectativas según las casas de apuestas, y de 0 o próximo a 0 para los equipos que hayan realizado una temporada muy por debajo de sus expectativas. La siguiente tabla muestra la eficiencia de los equipos. Asimismo, calculo los puntos esperados según las casas de apuestas y la diferencia entre puntos conseguidos y los puntos esperados. Así, una diferencia positiva significa que un equipo ha tenido un rendimiento por encima del previsto.
Tabla 1. Eficiencia de los equipos en La Liga primera vuelta 2024-2025
Hay tres equipos que destacan sobre el resto en su rendimiento: Atlético de Madrid, Mallorca y Athletic Club. Los tres con una eficiencia superior a 0,85. Con mal rendimiento destaca el Valencia que sólo ha obtenido 13 puntos de los 22 esperados.
Un resultado igual un tanto sorprendente para algunos lectores es la baja posición del Barcelona, que sólo tiene por debajo a equipos que han echado al entrenador (excepto el Getafe). Lo cual sugiere que los fríos números dicen que la primera vuelta del FC Barcelona en La Liga ha sido bastante mediocre. Alguno podría decir, bueno es que Flick ha conseguido que el equipo juegue muy bien y así ha aumentado los puntos esperados. Pues no, los puntos esperados según las casas de apuestas por el Barcelona de Flick en esta primera vuelta han sido de 39,6, mientras que los puntos esperados del Barca en la primera vuelta de la temporada 23-24 fueron 39,3! Es decir, prácticamente igual. Es posible que los números no reflejen la mejoría del Barcelona, o también es posible que la mejoría del Barca no sea tal. Veremos.
Con estos resultados se simula 10.000 veces la segunda vuelta generando así una distribución de probabilidades de quedar en cada una de las veinte posibles posiciones. Las simulaciones usan las cuotas de la primera vuelta para establecer las probabilidades para cada partido y así poder simular los partidos de tal forma de si la probabilidad de ganar del equipo local es 0,8 la probabilidad de que gane el partido en una simulación es del 80%. También se añade información de los resultados de la primera vuelta sumando un 40% de la diferencia entre puntos conseguidos y puntos realizados. Así, por ejemplo, el Atlético de Madrid tuvo 36 puntos esperados y 8 puntos más que los esperados por lo que los puntos esperados en la segunda vuelta serán 40 puntos esperados. Los resultados se presentan en una primera tabla que evalúa los puestos de honor, y una segunda, que analiza el descenso a La Liga 2.
Tabla 2. Probabilidades (%) de ganar la liga y clasificarse para Champions League a fecha 14/01/2025
En cuanto a las probabilidades de ganar La Liga tras la primera vuelta el Real Madrid tiene un 56,3%, el Atlético de Madrid tiene un 37,6%, el FC Barcelona un 5,7% y el Athletic Club de Bilbao un 0,3%. El Real Madrid tiene una probabilidad similar que al inicio de liga que era cercana al 55%. Los que sí han cambiado mucho sus probabilidades son el Atlético de Madrid que tras una gran primera vuelta pasa de un 10% a un 38%, mientras que el FC Barcelona pasa de un 34% a un 6%.
En cuanto a la Champions League tanto Real Madrid como Atlético de Madrid lo tienen casi hecho con probabilidades por encima del 99,9%, similar al FC Barcelona que tiene un 98,5%. El Athletic Club Bilbao lo tiene muy bien encarrilado estando por encima del 80% de probabilidades. Destacar la subida tanto del Atlético de Madrid desde un 90 a un 100%, y la del Athletic club de un 40 a un 80%. El principal damnificado es la Real Sociedad que ha pasado de un 26 a un 4%.
Tabla 3. Probabilidades (%) de descenso a fecha 14/01/2025
Los tres equipos que ocupan posición de descenso son los que más probabilidades tienen para ello: Valladolid 76,5%, Valencia 75,8% y Espanyol 59,8%. Tampoco se pueden despistar mucho Leganés (32,2%), Alavés (29,5) y Getafe (15,1). Aquí los cambios sí que han sido muy grandes puesto que el Valencia inició la campaña con pocas probabilidades de descenso (15%) y termina la primera vuelta con una probabilidad del 75%. En el cambio positivo están Las Palmas, Rayo Vallecano y Mallorca.
En este artículo se abordan dos cuestiones. En primer lugar, la eficiencia de los equipos en la primera vuelta de La Liga 2. Por otra parte, se realizan dos tipos de simulaciones: simulación de las posiciones finales teniendo en cuenta los resultados de la primera vuelta, y simular la liga completa con sus 42 jornada asumiendo que las cuotas de la primera vuelta darían la misma información para la primera vuelta y la segunda. Es decir, sería una simulación de las posiciones de la liga al comienzo de ésta.
Para calcular la eficiencia de los equipos sigo la metodología de este artículo que proporciona una eficiencia de 1 o próxima a 1 para los equipos que han realizado una temporada muy por encima de sus expectativas según las casas de apuestas, y de 0 o próximo a 0 para los equipos que hayan realizado una temporada muy por debajo de sus expectativas. La siguiente tabla muestra la eficiencia de los equipos. Asimismo, calculo los puntos esperados según las casas de apuestas y la diferencia entre puntos conseguidos y los puntos esperados. Así, una diferencia positiva significa que un equipo ha tenido un rendimiento por encima del previsto.
Tabla 1. Eficiencia de los equipos en La Liga 2 primera vuelta 2024-2025
Sin lugar a dudas, el equipo que mejor ha rendido dado lo que se esperaba de él ha sido el Mirandés, que parecía abocado a luchar por evitar el descenso y está peleando las posiciones de honor. Le siguen el Huesca y el Racing de Santander a pesar de su mala racha de resultados. Por abajo, el Tenerife es el líder indiscutible, si bien es cierto que no ha disputado dos partidos y se han supuesto sendos empates incluso con dos victorias seguiría siendo el equipo más ineficiente.
Con estos resultados se simula 1.000 veces la segunda vuelta así generando una distribución de probabilidades de quedar en cada una de las 22 posibles posiciones. Las simulaciones usan las cuotas de la primera vuelta para establecer las probabilidades para cada partido y así poder simular los partidos de tal forma de si la probabilidad de ganar del equipo local es 0,8 la probabilidad de que gane el partido en una simulación es del 80%. También se añade información de los resultados de la primera vía sumando un 40% de la diferencia entre puntos conseguidos y puntos realizados. Así, en la segunda vuelta la calidad del Mirandés le llevaría a unos puntos esperados de 29. Por último, se asume que en caso de llegar a la fase de ascenso la probabilidad de ascenso es del 25%.
Como ejemplo pongo el gráfico del Sporting de Gijón en el que se puede ver que lo más probable es que se quede en tierra de nadie entre el descenso y la lucha por el ascenso. El gráfico para todos los equipos puede descargarse en este enlace.
Tabla 2. Probabilidades de ascenso directo, ascenso, descenso La Liga 2 a fecha 26/12/2024
En cuanto a las probabilidades de ascender destaca el Almería (71,6%), seguido del Racing de Santander (58,1%), Elche (40,6%), Oviedo (33,3%), Mirandés (27,8%), y Granada (21,9%). El resto de equipos no llega ninguno al 15%. En la lucha por el descenso las simulaciones le dan al Cartagena y Tenerife casi descendidos con un 99,1% y 97,9% respectivamente. El Ferrol y Eldense también son claros candidatos para descender. Si bien en la mitad de las simulaciones no descienden estos cuatro equipos con lo que es muy posible que alguno se salve y otro equipo se vaya al pozo de 1ª RFEF.
En cuanto a los cambios en la probabilidad de ascender trascurrida la primera vuelta puede verse como los grandes beneficiados son el Racing de Santander y Almería aumentando sus probabilidades de ascenso en más de 30 puntos porcentuales. El Mirandés a pesar de haber sido el equipo más eficiente en la primera vuelta pasa de 0,4 en agosto a 15,7 en Navidades, aumentando así en 15,3 puntos porcentuales. El motivo es que el Almería y Racing de Santander ya eran de los equipos favoritos con lo que una primera vuelta bastante decente les catapulta como favoritos al ascenso.
Acaban de comenzar los Juegos Olímpicos de 2024 en París, y cuando concluyan correrán ríos de tinta para ver qué países lo han hecho mejor o peor en el medallero o en diplomas olímpicos (quedar entre los ocho primeros clasificados). España va con las expectativas bastante altas e incluso el presidente del Comité Olímpico Español habla sin tapujos de que es muy posible que se superen las 22 medallas de Barcelona ’92 donde España contaba con el factor casa que tradicionalmente logra un fuerte impulso en el medallero (ver por ejemplo este trabajo de Carlos Varela y coautores), impulso que se suele mantener en las siguientes ediciones de los Juegos pero que no es un impulso eterno.
Sin embargo, algunos trabajos como éste de Julio del Corral y coautores usan no sólo las medallas como output del desempeño olímpico sino también el número de participantes. Para la mayoría de deportistas clasificarse para unos Juegos Olímpicos ya es un logro en sí mismo, siendo escasas las plazas olímpicas a las que se renuncia teniendo derecho a ellas. Una excepción son las conocidas como mínimas de competitividad de la Real Federación Española de Atletismo, así como de otras federaciones, que hace que de facto atletas que hubiesen conseguido plaza a través del Ranking Olímpico les hagan renunciar a ella.
Por ello, vamos a analizar la eficiencia de los países produciendo participantes olímpicos. Es muy habitual que muchos medios recurran a lo que los economistas conocemos como producto medio para ver si un país lo ha hecho bien en términos de medallas o participantes. El producto medio no es otra cosa que dividir el número de participantes entre el PIB de un país o su población. Sin embargo, si la función de producción es cóncava, espóiler: lo es, los países más productivos saldrán del grupo de países pequeños. Esto es lo que se muestra en el siguiente gráfico donde puede verse la relación entre el producto medio del PIB y el PIB para los participantes de París 2024.
Como puede verse, de los quince países más grandes en términos de PIB ninguno presenta un producto medio elevado. Mucho mejor es realizar este tipo de análisis a través de la estimación de la eficiencia, que para no entrar en detalles muy técnicos, mide lo lejos o lo cerca que está un país de su máximo potencial de participantes dado su PIB. Esta frontera se puede estimar bien por modelos no paramétricos como el DEA o bien por métodos paramétricos como frontera estocástica. El siguiente gráfico muestra esta función de producción. Como se anticipó antes la función es cóncava, lo que indica que los crecimientos en la variable output (participantes) son cada vez menores a medida que un país aumenta su PIB. En concreto, la elasticidad del output es 0,66 que lleva a la concavidad de esta función.
En este caso ya es posible que países grandes estén cerca de la frontera como es el caso de España.
La siguiente tabla muestra la eficiencia de los países europeos en conseguir participantes en los Juegos Olímpicos de París 2024. Como es habitual, países ex comunistas lideran la lista: Serbia, Eslovenia, Montenegro, Hungría, Ucrania, Moldavia, y Croacia. España aparece en décimo lugar y primero de los países relativamente grandes en términos de PIB.
País
Código país
Eficiencia
País
Código país
Eficiencia
Serbia
SRB
0,85
Ireland
IRL
0,61
Slovenia
SLO
0,84
Kosovo
KOS
0,59
Montenegro
MNE
0,83
Armenia
ARM
0,57
Hungary
HUN
0,82
Norway
NOR
0,56
Ukraine
UKR
0,81
Portugal
POR
0,55
Republic of Moldova
MDA
0,78
Sweden
SWE
0,55
Croatia
CRO
0,78
Germany
GER
0,53
San Marino
SMR
0,75
Cyprus
CYP
0,51
Georgia
GEO
0,72
Great Britain
GBR
0,51
Spain
ESP
0,72
Monaco
MON
0,49
Lithuania
LTU
0,71
Switzerland
SUI
0,48
France
FRA
0,71
Israel
ISR
0,48
Azerbaijan
AZE
0,70
Austria
AUT
0,45
Greece
GRE
0,70
Finland
FIN
0,45
Netherlands
NED
0,69
North Macedonia
MKD
0,43
Poland
POL
0,68
Slovakia
SVK
0,40
Czechia
CZE
0,66
Albania
ALB
0,38
Latvia
LAT
0,66
Türkiye
TUR
0,36
Denmark
DEN
0,65
Andorra
AND
0,33
Belgium
BEL
0,65
Luxembourg
LUX
0,27
Italy
ITA
0,65
Malta
MLT
0,27
Romania
ROU
0,64
Bosnia & Herzegovina
BIH
0,23
Bulgaria
BUL
0,63
Iceland
ISL
0,22
Estonia
EST
0,62
Liechtenstein
LIE
0,13
Nota. Usamos el nombre que usa el COI en inglés.
Para ahondar en la relación entre eficiencia y PIB se muestra el siguiente gráfico que muestra el valor de la eficiencia de cada país en relación con su PIB.
Como puede verse España y Francia que como país organizador tiene garantizada una gran participación son los países grandes más eficientes, siendo Turquía el menos eficiente de los grandes.
Estos resultados podrían desgranarse en varios apartados. El primero y más lógico sería por cuestión de sexo, realizando un análisis para los participantes hombres y otro para participantes femeninos. España seguro que saldría bien parada pues lleva casi la misma representación en hombres que en mujeres. También se podría desgranar en un análisis para deportes de equipo, donde España saldría muy bien parada, y participantes individuales o de dobles, donde España posiblemente obtenga peores resultados.
En cualquier caso, vienen días de disfrutar y ojalá los deportistas españoles cosechen muchos éxitos.
Para calcular la eficiencia de los equipos sigo la metodología de este artículo que proporciona una eficiencia de 1 o próxima a 1 para los equipos que han realizado una temporada muy por encima de sus expectativas según las casas de apuestas, y de 0 o próximo a 0 para los equipos que hayan realizado una temporada muy por debajo de sus expectativas. La siguiente tabla muestra la eficiencia de los equipos. Asimismo, calculo los puntos esperados según las casas de apuestas y la diferencia entre puntos conseguidos y los puntos esperados. Así, una diferencia positiva significa que un equipo ha tenido un rendimiento por encima del previsto.
Equipo
Eficiencia
Puntos
Puntos esperados
Diferencia
Leganés
0,96
74
60,6
13,4
Racing de Santander
0,83
64
56,9
7,1
Real Valladolid
0,79
72
66,0
6,0
Racing de Ferrol
0,75
59
54,2
4,8
Sporting de Gijón
0,73
65
60,5
4,5
Burgos
0,71
59
55,1
3,9
Cartagena
0,69
51
47,8
3,2
Real Oviedo
0,63
64
61,9
2,1
Eibar
0,62
71
69,1
1,9
Amorebieta
0,59
45
44,0
1,0
RCD Espanyol
0,55
69
68,5
0,5
CD Eldense
0,54
50
49,8
0,2
Mirandés
0,52
49
49,2
-0,2
Levante
0,46
59
60,3
-1,3
SD Huesca
0,37
49
52,2
-3,2
Villarreal B
0,37
43
46,3
-3,3
Alcorcón
0,36
44
47,3
-3,3
CD Tenerife
0,33
56
60,1
-4,1
Elche CF
0,23
59
65,5
-6,5
Real Zaragoza
0,20
51
58,2
-7,2
Albacete
0,14
51
60,2
-9,2
FC Andorra
0,06
43
56,0
-13,0
Sin lugar a dudas, el equipo que mejor ha rendido dado lo que se esperaba de él ha sido el Leganés, que ha conseguido el ascenso directo. Le siguen el Racing de Santander que pese a la gran temporada no ha logrado clasificarse ni siquiera para los play-off, y el Real Valladolid comandados por el polémico Pezzolano. Por abajo se encuentran el descendido FC Andorra seguido del Albacete y el Zaragoza, equipos que han estado jugando con fuego hasta casi la última jornada.
Una vez concluida la primera vuelta de La Liga de la temporada 2023-2024 es un buen momento para analizar lo sucedido y ver qué puede suceder al concluir la temporada. Para analizar lo sucedido se calcula la eficiencia de los equipos en el campo. La eficiencia en el campo se calcula comparando los puntos logrados con los puntos que se esperaban según las cuotas de las casas de apuestas. De esta forma se obtiene tanto la diferencia entre los puntos conseguidos y los esperados como una nota entre 0 y 1, donde cero supone hacerlo peor que la peor expectativa, y 1 supone batir la mejor expectativa de puntos. Por otra parte, para calcular las probabilidades a fin de temporada se usan las cuotas de la primera vuelta, se simulan 1000 veces, y se les suma la puntuación obtenida en la primera más un tercio de la diferencia entre puntos conseguidos y puntos esperados. Dada la espectacular primera vuelta del Girona el análisis se centrará en este equipo. Varias preguntas surgen: ¿Cómo de espectacular ha sido la primera vuelta del Girona? ¿Cómo de improbable era que el Girona terminase entre los dos primeros? ¿y ser segundo con 48 puntos? ¿Cómo de posible es que se repita la hazaña del Leicester? En este artículo se tratará de dar respuesta a estas preguntas y alguna más.
Análisis de la primera vuelta
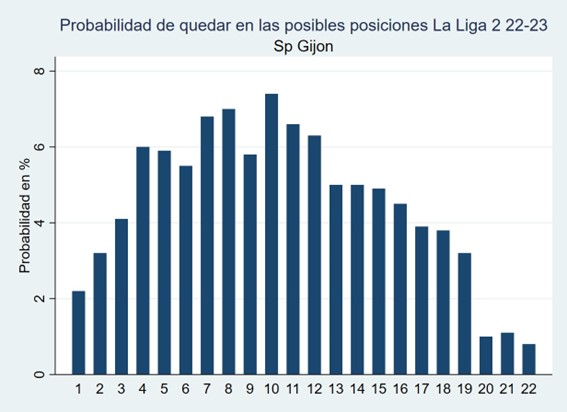
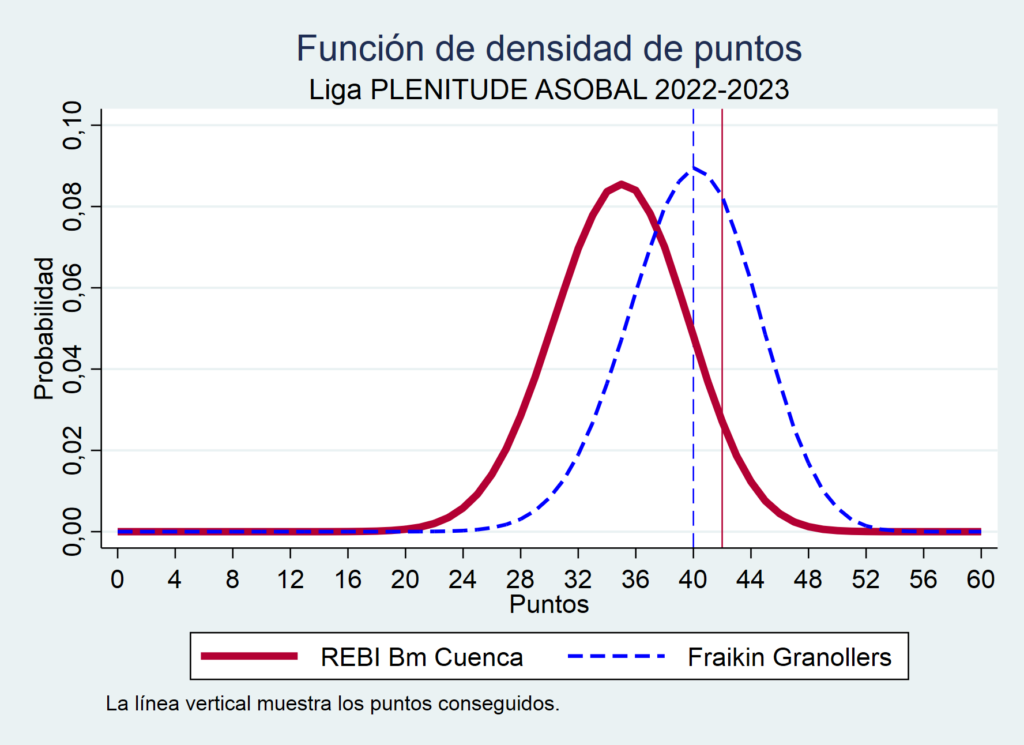
El análisis comienza calculando la probabilidad de obtener cada una de las posibles puntuaciones en función de las cuotas de los partidos de la primera vuelta. El siguiente gráfico muestra el caso del Girona, donde se puede ver que la probabilidad de obtener más puntos que los realmente obtenidos es virtualmente 0.
Gráfico 1. Función de densidad de victorias del Girona en la primera vuelta 2023-2024
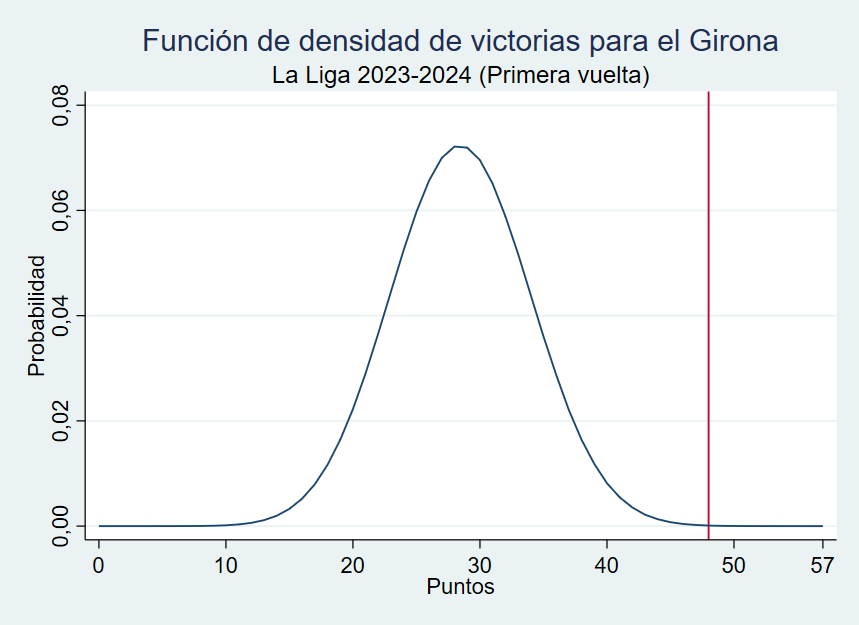
En concreto, la siguiente tabla muestra las probabilidades de obtener todas las puntuaciones posibles por el Girona en esta primera vuelta por encima de los puntos realmente conseguidos.
Tabla 1. Probabilidades para el Girona de más de 48 puntos (1ª vuelta de La Liga 2023-2024)
Puntos
Probabilidad
49
0,00004960
50
0,00002380
51
0,00000833
52
0,00000407
53
0,00000135
54
0,00000033
55
0,00000021
57
0,00000002
Suma
0,000088
Puede verse como la probabilidad de todas estas puntuaciones es virtualmente cero con lo que la suma de ellas también lo es. Para calcular la eficiencia del Girona en esta primera vuelta lo único que hay que hacer es calcular la resta de uno menos la suma de las probabilidades de puntuar más que lo que se hizo, en este caso 0,000088. Por lo que la eficiencia del Girona es 0,99991.
La siguiente tabla muestra la diferencia entre puntos y puntos esperados, así como el valor de la eficiencia.
Tabla 2. Eficiencia en la primera vuelta de La Liga 2023-2024
Equipo
Puntos
Puntos esperados
Diferencia
Eficiencia
Girona
48
28,5
19,5
0,99991
Real Madrid
48
39,4
8,6
0,97
Athletic Bilbao
38
31,6
6,4
0,90
Las Palmas
25
19,6
5,4
0,88
Getafe
26
22,1
3,9
0,81
Betis
28
25,0
3,0
0,74
Atlético de Madrid
38
35,4
2,6
0,71
Barcelona
41
39,4
1,6
0,65
Valencia
26
24,9
1,1
0,62
Rayo Vallecano
23
22,6
0,4
0,57
Real Sociedad
32
32,1
-0,1
0,53
Osasuna
22
23,9
-1,9
0,40
Mallorca
18
21,6
-3,6
0,28
Alavés
17
20,6
-3,6
0,28
Cádiz
15
18,8
-3,8
0,26
Villarreal
19
26,4
-7,4
0,10
Granada
11
19,0
-8,0
0,07
Celta de Vigo
16
25,0
-9,0
0,05
Sevilla
16
26,9
-10,9
0,03
Almería
5
18,0
-13,0
0,00
Los equipos que los están haciendo bastante mejor de lo esperado son Las Palmas, Athletic de Bilbao, Real Madrid y Girona, todos ellos con más de cinco puntos de diferencia positiva entre puntos conseguidos y puntos esperados. Por el contrario, hay cinco equipos que los están haciendo bastante peor de lo esperado: Villarreal, Granada, Celta de Vigo, Sevilla y Almería.
El Leicester obtuvo un valor de eficiencia en la Premier Legue 2015-2016 de 0.99987, como puede verse en este artículo que publiqué hace unos años, que hace que sean muy similares, siendo un poquito superior la del Girona si bien es sólo en una vuelta.
Simulando esta primera vuelta 1.000 usando las cuotas para obtener probabilidades en cada partido se obtienen algunos resultados interesantes. En primer lugar, puede verse como la probabilidad de que el Girona estuviese entre los dos primeros equipos clasificados al final de la primera vuelta era del 3,3%. Probabilidad baja pero no imposible, pues implica que cada 30 ligas en una se situaría en los dos primeros puestos. Los gráficos del resto de equipos pueden verse en este enlace.
Gráfico 2. Probabilidades del Girona en la 1ª vuelta de La Liga 2023-2024 en 1.000 simulaciones
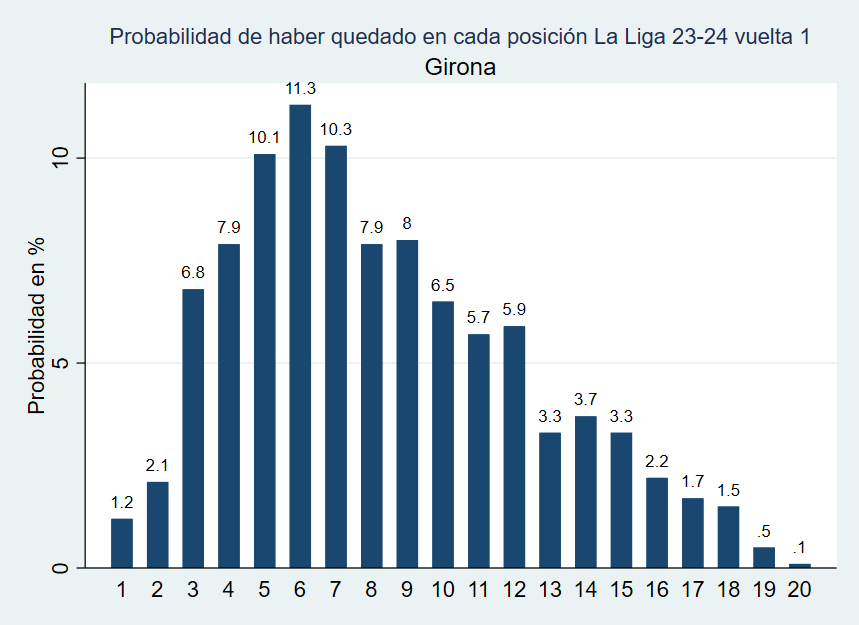
En segundo lugar, un hecho que puede sorprender es que el Girona ocupe la segunda plaza con 48 puntos. Y sí, debería hacerlo pues en sólo cuatro simulaciones de las 1.000 realizadas un equipo con 48 puntos no ocupa el primer lugar, y en las cuatro era el Real Madrid el segundo siendo el primero el FC Barcelona. De hecho la mayoría de las veces se consigue la primera posición con menos de 48 puntos.
Gráfico 3. Puntuaciones en la 1ª vuelta de La Liga 2023-2024 en 1.000 simulaciones de los cuatro primeros equipos clasificados
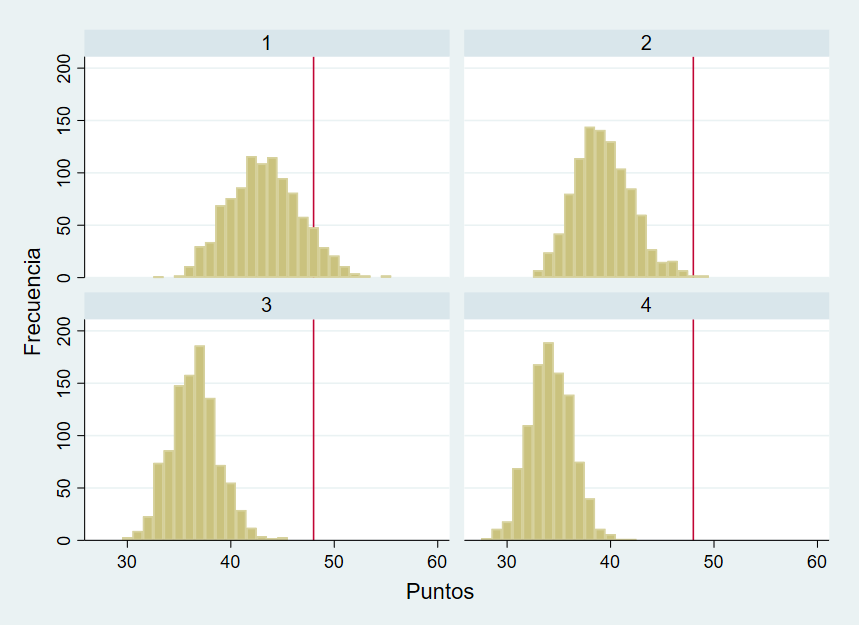
¿Qué puede pasar al final de liga?
La pregunta que todos los aficionados tenemos en mente es ¿Puede repetir el Girona la gesta del Leicester? Como se puede ver en este artículo ya mencionado en la temporada 2015-2016 de la Premier se dio conjuntamente una grandísima actuación del Leicester, pero es que también ninguno de los equipos grandes tuvo una buena actuación. Por el contrario, el Girona se está enfrentando a una gran actuación del Real Madrid con 9 puntos conseguidos más de los esperados, y con una buena actuación del Atlético de Madrid y del FC Barcelona ambos con más puntos de los esperados.
Para intentar responder a esta pregunta uso las simulaciones de la primera vuelta, pues obviamente no están disponibles las cuotas para los partidos de la segunda vuelta. A estas simulaciones les añado los puntos conseguidos en la primera vuelta, y un tercio de la diferencia de puntos entre los conseguidos y los esperados pues es razonable pensar que por ejemplo el Girona es mejor equipo de lo que mostraban las cuotas especialmente de los primeros partidos. Los empates a puntos los resuelvo por sorteo.
La siguiente tabla muestra el porcentaje en los que cada equipo se sitúa en cada una de las 20 posibles posiciones al final de La Liga 2023-2024 tras las 1.000 simulaciones mencionadas.
Tabla 3. Probabilidades de las posiciones al final de La Liga 2023-2024 tras 1.000 simulaciones
Equipo
P1
P2
P3
P4
P5
P6
P7
P8
P9
P10
P11
P12
P13
P14
P15
P16
P17
P18
P19
P20
Real Madrid
77
18
5
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Girona
13
39
30
14
3
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Barcelona
9
34
39
13
4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Ath Madrid
1
6
16
41
27
8
1
0
0
0
0
0
0
0
0
0
0
0
0
0
Ath Bilbao
0
3
9
27
46
14
1
0
0
0
0
0
0
0
0
0
0
0
0
0
Sociedad
0
0
1
4
19
63
10
3
1
0
0
0
0
0
0
0
0
0
0
0
Villarreal
0
0
0
0
0
0
2
5
9
12
12
13
13
11
9
6
5
3
1
0
Betis
0
0
0
0
1
9
37
21
13
8
5
4
1
1
0
0
0
0
0
0
Osasuna
0
0
0
0
0
0
4
7
10
11
14
13
14
12
8
4
2
1
0
0
Vallecano
0
0
0
0
0
0
5
10
13
12
13
13
12
11
6
3
2
1
0
0
Getafe
0
0
0
0
0
2
14
16
16
17
13
8
6
4
2
1
0
0
0
0
Valencia
0
0
0
0
0
3
20
23
17
13
8
8
4
2
1
1
0
0
0
0
Las Palmas
0
0
0
0
0
1
6
12
14
14
14
15
11
6
4
3
1
0
0
0
Sevilla
0
0
0
0
0
0
0
0
2
3
6
7
12
14
15
15
14
8
2
0
Celta
0
0
0
0
0
0
0
1
2
2
5
8
8
13
16
18
14
10
4
0
Mallorca
0
0
0
0
0
0
0
1
2
3
5
7
11
12
17
17
14
9
2
0
Alavés
0
0
0
0
0
0
0
0
1
2
4
3
7
10
15
18
21
16
4
1
Cádiz
0
0
0
0
0
0
0
0
0
1
1
1
2
5
6
11
22
35
15
2
Granada
0
0
0
0
0
0
0
0
0
0
0
0
1
0
2
4
6
16
57
14
Almería
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2
15
83
Para los cuatro equipos que están luchando se de forma más clara se ve en el siguiente gráfico.
Gráfico 4 Probabilidades de las posiciones al final de La Liga 2023-2024 tras 1.000 simulaciones (Real Madrid, Girona, FC Barcelona y Atlético de Madrid)
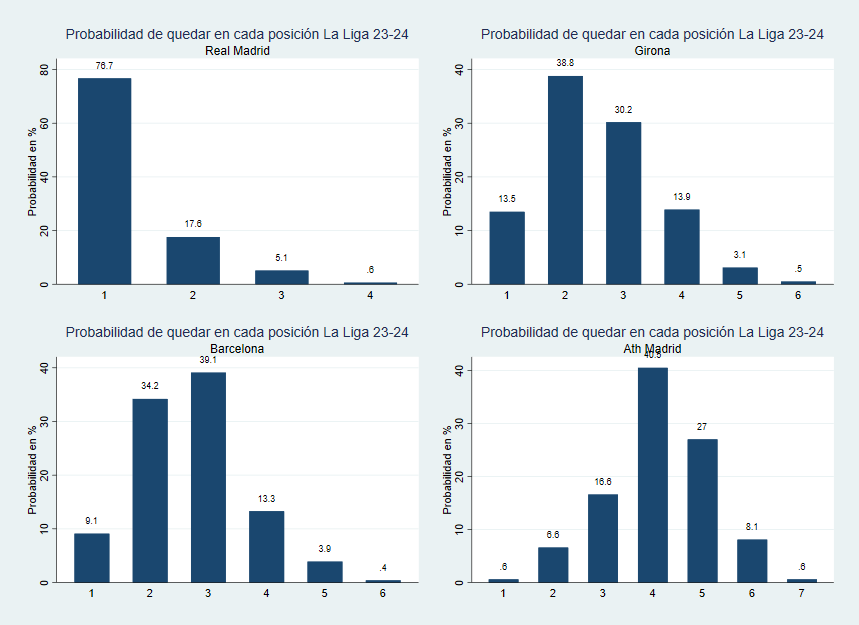
Puede verse como la probabilidad de victoria del Girona es del 13,4 %. Probabilidad que hubiese firmado cualquier aficionado del Girona, pues al principio de liga era virtualmente cero. Así que sí, es posible un nuevo Leicester pero sólo sucedería en una cada 8 ligas con lo que lo más normal es que no suceda. Decir, que las probabilidades a ganador son muy similares a las que salen de la apuesta a ganador de liga: Real Madrid 74%, Girona 12%, FC. Barcelona 10% y Atlético de Madrid 3%.
Por último se pone una tabla con las probabilidades de cada equipo de conseguir cada uno de los objetivos. Destacar la lucha que parece que va a haber entre el Atlético de Madrid con los principales equipos vascos para conseguir la única posición de Champions con algo de incertidumbre. Por abajo, Granada y Almería lo tienen muy complicado para mantener la categoría, y hay varios equipos que no se han librado, destaca el Sevilla con más de un 10% de probabilidad de descender.
Tabla 4. Probabilidades de ítems al final de La Liga 2023-2024 tras 1.000 simulaciones
Una vez concluida la primera vuelta de La Liga Hypermotion de la temporada 2023-2024 y con el parón navideño es un buen momento para analizar lo sucedido y ver qué puede suceder al concluir la temporada. Para analizar lo sucedido se van a calcular la eficiencia de los equipos en el campo y lo que se espera que suceda a fin de liga. Para calcular la eficiencia en el campo se compara los puntos logrados con los puntos que se esperaban según las cuotas de las casas de apuestas. De esta forma se obtiene tanto la diferencia entre los puntos conseguidos y los esperados como una nota entre 0 y 10, donde cero supone hacerlo peor que la peor expectativa, y 10 supone batir la mejor expectativa de puntos. Por otra parte, para calcular las probabilidades a fin de temporada se usan las cuotas de la primera vuelta, se simulan 1000 veces, y se les suma la puntuación obtenida en la primera más un tercio de la diferencia entre puntos conseguidos y puntos esperados.
Eficiencia en el campo
Para evaluar la eficiencia en el campo uso la metodología desarrollada en este artículo del Journal of Sports Economics. La metodología, en versión resumida, consiste en coger las cuotas de las apuestas deportivas, se pasan estas cuotas a probabilidades, con las probabilidades de victoria, empate y derrota se puede calcular la probabilidad de cada una de las posibles puntuaciones, que en la primera vuelta de la Liga2 van desde 0 hasta 63. Después se suman las probabilidades de las puntuaciones superiores a la realmente obtenida y ese valor se resta de uno. Por ejemplo, un equipo que obtuviese 61 puntos, y que la probabilidad de haber obtenido 63 puntos era de 0,01 su eficiencia sería 0,99.
La siguiente tabla muestra la eficiencia en el campo de la primera vuelta en la Liga 2 en la temporada 2023/2024.
Tabla 1. Eficiencia en el campo en la primera vuelta La Liga 2 2023-2024
Equipo
Puntos
Puntos esperados
Diferencia
Eficiencia
Ferrol
37
27,0
10,0
0,97
Leganés
39
29,4
9,6
0,96
Sp Gijón
35
29,9
5,1
0,84
Santander
33
28,0
5,0
0,83
Burgos
30
26,1
3,9
0,79
Mirandés
28
24,1
3,9
0,78
Valladolid
35
32,7
2,3
0,69
Eldense
26
24,2
1,8
0,66
Levante
32
30,2
1,8
0,65
Oviedo
30
29,2
0,8
0,59
Villarreal B
24
23,6
0,4
0,58
Tenerife
31
30,7
0,3
0,56
Espanyol
34
35,5
-1,5
0,43
Zaragoza
28
29,9
-1,9
0,41
Eibar
32
34,4
-2,4
0,37
Elche
30
32,8
-2,8
0,35
Huesca
22
25,9
-3,9
0,28
Alcorcón
20
24,6
-4,6
0,23
Andorra
23
28,5
-5,5
0,19
Albacete
25
31,5
-6,5
0,15
Amorebieta
15
22,2
-7,2
0,10
Cartagena
15
24,3
-9,3
0,05
Los tres mejores equipos son Racing de Ferrol, Leganés y Sporting de Gijón. Muy destacable es la actuación del líder Leganés pero especialmente la del Racing de Ferrol que su expectativa era estar en la parte media baja de la clasificación y ha obtenido más de 10 puntos que los esperados. Por el lado contrario, los peores equipos han sido Albacete, Amorebieta y Cartagena. Destacar al Albacete que su expectativa era ser el tercer equipo con más puntos y sin embargo está situado en la parte media-baja de la clasificación.
Las probabilidades a fin de liga
Para simular lo que queda de liga he realizado lo siguiente. He cogido la puntuación de la primera vuelta, y le he añadido un tercio de la diferencia entre puntos obtenidos y puntos esperados. Por ejemplo, en el caso del Racing de Ferrol y del Leganés son tres puntos adicionales. El motivo es que para simular la competición cojo las probabilidades de los partidos de la primera vuelta y es razonable pensar que parte de ese rendimiento por encima o por debajo de lo esperado se mantenga en el tiempo. Es razonable pensar que el Leganés no es el mejor equipo de la liga para la segunda vuelta pero tampoco lo es pensar que es un mero equipo de media tabla. Con esos dos supuestos: puntos añadidos y uso de probabilidades de la primera vuelta se simula la competición 1.000 veces obteniendo así la probabilidad de cada equipo de terminar en cada una de las 22 posibles posiciones. Decir, que en caso de empate a puntos en la simulación se decide por sorteo el orden de los equipos
La siguiente tabla muestra la probabilidad de cada equipo de terminar en cada una de las posibles posiciones al finalizar la Liga 2 temporada 2023-2024.
Tabla 2. Probabilidad de terminar en cada posición a la conclusión de La Liga 2 2023-2024 tras primera vuelta (1.000 simulaciones)
Equipo
P 1
P 2
P 3
P 4
P 5
P 6
P 7
P 8
P 9
P 10
P 11
P 12
P 13
P 14
P 15
P 16
P 17
P 18
P 19
P 20
P 21
P 22
Leganés
52,6
23,5
11,0
6,2
2,9
1,5
1,0
1,0
0,3
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
Valladolid
21,5
24,7
19,2
10,4
8,5
5,3
4,4
2,6
2,1
0,3
0,4
0,5
0,1
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
Espanyol
7,5
13,8
13,2
15,6
11,6
12,1
8,1
6,0
4,5
3,0
2,0
1,4
0,7
0,3
0,1
0,0
0,1
0,0
0,0
0,0
0,0
0,0
Sp Gijón
7,2
16,2
16,9
13,4
12,8
9,4
8,9
5,2
4,6
2,9
1,1
0,7
0,3
0,3
0,1
0,0
0,0
0,0
0,0
0,0
0,0
0,0
Ferrol
4,8
7,2
11,3
12,6
12,1
13,7
9,5
10,4
6,5
5,0
2,6
2,8
1,2
0,2
0,1
0,0
0,0
0,0
0,0
0,0
0,0
0,0
Santander
1,8
5,2
7,6
10,1
10,9
10,9
12,5
10,4
9,4
6,4
6,2
3,4
3,4
1,1
0,4
0,3
0,0
0,0
0,0
0,0
0,0
0,0
Eibar
1,8
3,6
7,5
11,2
12,8
11,1
12,8
10,8
8,7
7,0
4,6
3,3
2,5
1,3
0,7
0,2
0,0
0,1
0,0
0,0
0,0
0,0
Levante
1,7
3,4
6,3
8,1
9,1
11,0
10,2
11,5
12,5
8,7
8,1
4,3
2,0
1,2
1,0
0,5
0,3
0,1
0,0
0,0
0,0
0,0
Elche
0,5
1,1
1,9
3,9
6,0
6,7
10,2
9,6
11,0
13,0
11,0
9,3
7,1
5,4
1,2
1,5
0,5
0,1
0,0
0,0
0,0
0,0
Tenerife
0,5
0,9
3,8
5,6
7,9
7,6
8,7
14,1
10,8
10,9
9,1
8,6
4,6
4,3
1,7
0,6
0,3
0,0
0,0
0,0
0,0
0,0
Burgos
0,1
0,1
0,2
1,3
2,3
3,3
3,9
5,8
8,0
11,2
13,4
15,2
11,8
9,1
8,7
3,4
1,8
0,3
0,1
0,0
0,0
0,0
Oviedo
0,0
0,1
1,1
1,3
1,7
4,4
4,5
5,1
9,8
13,0
13,9
13,3
11,4
10,8
4,8
3,1
1,2
0,4
0,1
0,0
0,0
0,0
Mirandés
0,0
0,1
0,0
0,2
0,2
0,4
1,3
1,5
3,4
4,0
6,3
8,5
11,7
16,4
16,8
15,2
9,3
3,6
1,1
0,0
0,0
0,0
Zaragoza
0,0
0,1
0,0
0,1
0,9
1,9
2,7
4,7
5,2
7,7
11,5
12,9
16,8
11,6
10,3
8,2
3,4
1,5
0,4
0,0
0,1
0,0
Amorebieta
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,2
0,9
5,4
18,0
31,2
44,3
Cartagena
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,1
0,5
0,8
5,3
18,5
33,0
41,8
Villarreal B
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,2
0,1
0,2
0,5
0,7
1,7
3,0
5,7
11,9
18,9
30,2
20,5
4,6
1,7
0,1
Albacete
0,0
0,0
0,0
0,0
0,2
0,3
0,7
0,5
2,1
4,0
5,7
7,7
11,5
16,4
18,2
16,0
10,0
5,2
1,2
0,2
0,1
0,0
Alcorcón
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,3
0,4
2,1
5,3
16,6
35,6
27,0
12,7
Eldense
0,0
0,0
0,0
0,0
0,1
0,4
0,6
0,6
0,8
2,2
3,2
5,8
8,9
12,2
17,3
18,8
15,6
8,9
3,8
0,8
0,0
0,0
Huesca
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,1
0,0
0,2
0,7
0,6
1,5
4,4
10,8
18,9
36,1
19,4
6,2
1,1
Andorra
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,2
0,4
0,4
1,4
3,6
5,8
11,1
15,4
25,0
23,7
9,4
2,9
0,7
0,0
Puede verse como el Leganés y el Valladolid tienen muy bien encaminado lograr el ascenso directo, pero no pueden dormirse mucho Sporting de Gijón, Espanyol y Racing de Ferrol están al acecho.
Por comparar estas probabilidades con algo he visto que bwin ofrece las cuotas a ganador de la Liga 2. Como puede verse aunque tienen cierto parecido difieren bastante pues bwin le otorga una probabilidad de ganar La Liga 2 al Leganés del 26%, mientras que en el modelo que he empleado es de más del 50%. He hecho alguna prueba cambiando la proporción de la diferencia entre puntos conseguidos y puntos esperados y lógicamente cuanto mayor fuese esa cifra mayor era la cifra de la probabilidad de ser el campeón del Leganés. Si mi modelo es bueno, aquí habría lo que se conoce como una apuesta con valor pues la probabilidad de que gane el Leganés según mi modelo es de más del 50% y lo pagan como si fuese del 31%, teniendo en cuenta el overround.
Tabla 3. Cuota y probabilidad de ganar LaLiga2 2023-2024 según bwin tras primera vuelta
Equipo
Cuota ganador liga 2 bwin
Probabilidad
Leganés
3,25
25,67
Espanyol
8
10,43
Valladolid
6,5
12,84
Sp Gijón
8
10,43
Eibar
13
6,42
Ferrol
8
10,43
Levante
15
5,56
Elche
26
3,21
Santander
17
4,91
Tenerife
21
3,97
Burgos
41
2,03
Albacete
151
0,55
Zaragoza
67
1,25
Oviedo
51
1,64
Mirandés
0,00
Eldense
251
0,33
Cartagena
0,00
Amorebieta
0,00
Villarreal B
501
0,17
Alcorcón
0,00
Huesca
0,00
Andorra
501
0,17
Para concluir he agrupado en cuatro tipos de puestos: ascenso directo, fase de ascenso, posiciones 7-18 y descenso. Asumiendo que la probabilidad de los cuatro clasificados para la fase es la misma se puede calcular la probabilidad de ascenso. Puede verse como el Leganés lo tiene muy bien encamidado, pero Espanyol, Valladolid, Sporting de Gijón y Eibar se sitúan por encima del 25%.
Tabla 4. Probabilidad tras 1.000 simulaciones de resultado en La Liga 2 2023-2024
Aunque no es de actualidad creo que es un análisis que puede resultar interesante. Con las cuotas de las apuestas deportivas, en concreto he cogido para cada partido el promedio de casas de apuestas que proporciona la web https://www.football-data.co.uk/, he realizado 1.000 simulaciones de La Liga 2 de la temporada 2022-2023. Así, puede calcularse la probabilidad de quedar en cada una de las 22 posibles posiciones que viene determinado por el número de veces que queda en una determinada posición dividido por el número de simulaciones. Por ejemplo, si un equipo queda en primera posición en 10 simulaciones pues tendrá un 1% de haber quedado en primera posición. De ahí, es fácil a las probabilidades de descenso (cuatro últimas posiciones), y de mantenerse (posiciones 7-18). Algo más complicado es calcular la probabilidad de ascenso pues los dos primeros suben directamente pero del 3 al 6 disputan un play-off. Por simplicidad, se asume que la probabilidad de subir en el play-off es la misma para los cuatro equipos. Así, la probabilidad de subir es la probabilidad de quedar en las dos primeras posiciones más el 25% de quedar entre la tres y la seis.
Tabla 1. Probabilidad en % de cada posición en 1.000 simulaciones La Liga 2 2022-23
Equipo
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Eibar
25
17
13
10
9
6
5
4
3
2
2
1
1
1
1
0
0
0
0
0
0
0
Granada
18
15
14
10
8
8
6
5
4
3
3
2
1
1
1
1
0
0
0
0
0
0
Las Palmas
16
15
13
11
7
8
5
5
6
4
2
3
2
1
1
1
0
0
0
0
0
0
Eibar
15
15
11
10
9
8
6
6
4
4
4
2
2
1
2
1
1
0
0
0
0
0
Alavés
10
13
13
10
10
7
6
7
5
4
3
3
3
2
1
1
1
1
1
0
0
0
Tenerife
5
4
5
8
8
8
8
7
6
7
6
6
4
3
3
4
2
2
2
1
1
1
Zaragoza
2
3
5
7
6
7
7
9
8
6
6
7
5
4
5
3
3
3
2
2
2
0
Sp Gijón
2
3
4
6
6
6
7
7
6
7
7
6
5
5
5
5
4
4
3
1
1
1
Cartagena
2
2
2
3
5
5
6
4
8
7
6
7
6
7
6
5
5
4
5
2
3
1
Leganés
1
3
4
4
6
5
9
7
6
6
6
7
6
5
5
4
4
3
2
3
1
1
Albacete
1
2
3
6
6
6
6
8
7
7
6
6
7
6
4
6
4
3
3
3
1
1
Andorra
1
2
3
2
4
6
6
6
6
6
8
6
7
7
6
7
7
5
4
2
2
1
Huesca
1
1
1
1
3
4
4
4
5
5
6
5
7
7
7
8
7
7
5
6
5
2
Oviedo
1
2
4
4
5
6
7
6
6
7
6
7
7
6
5
4
4
4
2
3
3
1
Santander
0
0
1
2
2
3
2
3
5
5
6
6
5
7
8
7
9
7
8
5
6
4
Villarreal B
0
0
1
1
1
1
2
2
3
3
4
4
5
6
5
8
6
10
9
11
9
9
Burgos
0
0
1
1
2
2
3
4
4
4
7
6
5
6
8
7
7
10
8
8
5
5
Ponferradina
0
0
0
1
1
1
2
2
2
4
3
4
5
5
6
8
8
8
9
12
9
11
Mirandés
0
0
0
1
1
1
2
1
2
3
3
4
5
6
7
7
9
9
10
11
11
8
Málaga
0
0
1
2
2
3
3
3
3
6
5
6
5
7
8
8
7
7
9
6
6
4
Ibiza
0
0
0
0
1
1
1
1
1
2
2
2
4
4
5
5
8
8
9
14
17
16
Lugo
0
0
0
0
0
0
0
0
0
1
1
1
2
3
2
3
5
6
9
12
19
36
Nota: Los equipos aparecen ordenados por las probabilidades de quedar en las tres primeras posiciones.
Como en esta tabla es complicado de ver cómo evolucionan las probabilidades se pueden descargar los gráficos similares a éste del Sporting en este enlace:
Por último, se muestra las probabilidades de cada equipo de los tres posibles resultados: subir, mantenerse y bajar.
Tabla 2. Probabilidad en % de resultados en 1.000 simulaciones La Liga 2 2022-23
Estos días se está celebrando el Mundial de Balonmano femenino, campeonato que hace cuatro años la selección española apodada como “Las Guerreras” se quedó a las puertas de vencer. Sin embargo, en esta edición ha quedado apeada en la conocida como Main Round al no quedar entre los dos primeros puestos de su grupo que daban acceso a los cuartos de final. Es obvio que es una decepción para la afición española, pero cuánto tiene de resultado esperable no haber llegado a los cuartos de final.
Para responder a esta pregunta he cogido las cuotas de las apuestas a los partidos de los partidos valederos para la Main Round y he simulado los resultados del grupo 10.000 veces. De esta forma se puede ver la probabilidad de haber quedado en cada uno de las seis posible posiciones del grupo. Hay que tener en cuenta que las dos primeras clasificadas pasaban a cuartos de final y por tanto avanzaban en el torneo. Así para conocer la probabilidad de pasar de grupo basta con sumar la probabilidad de haber quedado en primera y segunda posición. La siguiente tabla muestra las probabilidades para las seis selecciones.
Equipo
Posición real
Posición 1
Posición 2
Posición 3
Posición 4
Posición 5
Posición 6
Países Bajos
1
87,2%
10,7%
1,8%
0,3%
0,0%
0,0%
España
4
7,5%
44,3%
31,1%
15,5%
1,5%
0,2%
Brasil
3
3,4%
27,1%
32,3%
30,8%
5,1%
1,3%
Rep. Checa
2
2,0%
17,7%
32,4%
40,4%
6,5%
1,0%
Ucrania
6
0,0%
0,1%
1,0%
5,1%
32,3%
61,5%
Argentina
5
0,0%
0,2%
1,3%
7,9%
54,6%
36,1%
Como puede verse España contaba con apenas un 7,5 % de quedar en primera posición, por un 44,3 % de probabilidad de obtener la segunda plaza. Así, la probabilidad de conseguir un billete era un 51 %, es decir un cara o cruz que salió cruz. En España hay una corriente que piensa que España como ha cosechado éxitos en el pasado tanto en el Mundial como en Juegos Olímpicos sigue siendo una de las favoritas, pero la realidad es muy tozuda y no muestra esto. Por el contrario, Países Bajos, sin duda la selección de más nivel del grupo, tenía casi un 98 % de probabilidad de pasar a cuartos de final.
España quedó cuarta de grupo, que dado que quinta y sexta la probabilidad era muy baja es la peor posición de las razonablemente posibles. Con lo que España no debería estar contenta con su rendimiento. Pero tampoco debe pensar que su nivel es un nivel de favorita y que se va a colocar en cuartos de final con toda probabilidad.
Algunos detalles técnicos de la metodología
Las cuotas de apuestas se recogieron de la web oddsportal.com, que recoge el promedio de las cuotas de varias casas de apuestas. Para pasar las cuotas a probabilidades se usó la calculadora que proporciona la web football-data.co.uk, usando en concreto su metodología de oddsratio por la ventaja que supone al haber algunos partidos con cuotas muy desequilibradas.
En este enlace se da acceso a los datos recopilados y al do-file de Stata usado para realizar los cálculos. También decir que se podría haber hecho un análisis algo más fino modelizando no sólo si se consigue una victoria, empate o derrota sino modelizando las diferencias en el marcador que podrían servir para deshacer desempates. Por simplicidad en caso de empate se ha desempatado usando un sorteo. Creo, no obstante que los resultados poco cambiarían y que las probabilidades de pasar de grupo o quedarse fuera para España eran similares
