Anuncios
Anuncios: (ver Moodle)
Organización
Asignatura de Tercer Curso – Primer Cuatrimestre.
Fechas de los Exámenes Parciales: (ver Moodle)
Referencias
Bibliografía Básica
CHAVES, E.W.V.(2007). “”Mecánica del Medio Continuo. Conceptos Básicos“. CIMNE-Barcelona, ISBN: 978-84-96736-38-2.
CHAVES, E.W.V.(2009). “”Mecánica del Medio Continuo. Modelos Constitutivos“. CIMNE-Barcelona, ISBN:978-84-96736-68-9.
Oliver, X. & Agelet de Saracibar,C. (2000). Mecánica de Medios Continuos para Ingenieros. Edicions UPC- Barcelona. ISBN: 84-8301-412-2.
Mase, G.E. (1977). Mecánica del Medio Continuo. McGraw-Hill, USA.
Bibliografía Complementaria
Malvern, L. (1969). An Introduction to the Mechanics of a Continuous Medium. Prentice-Hall.
Spencer, A.J.M. (1980). Continuum Mechanics, Longman.
Truesdell, C. & Noll, W. (1965). The Non-Linear Field Theories of Mechanics. in Encyclopedia of Physics, Vol. III/3, Springer.
Gurtin, M.E. (1981). Topics in Finite Elasticity. SIAM.
Holzapfel, G.A. (2000). Nonlinear solid mechanics. John Wiley & Sons Ltd. England.
Díaz del Valle, J. (1984). Mecánica de los Medios Continuos I. Servicio de publicaciones E.T.S. de Ingenieros de Caminos, C. y P. Santander.
Antman, S.S. (1995). Nonlinear Problems of Elasticity. Springer-Verlag.
Lai, W.M.; Rubin, D. & Krempl, E. (1978). Introduction to Continuum Mechanics. Pergamon Press.
Chadwick, P. (1976). Continuum Mechanics. George Allen and Unwin.
Chadwick, P. (1999). Continuum Mechanics:Consice Theory and Problems. Dover Reprint.
Ogden, R.W. (1984). Nonlinear Elastic Deformations. John Wiley (Dover reprint).
Marsden, J.E. & Hughes, T.J.R. (1983). Mathematical Foundation of Elasticity. Prentice Hall (Dover reprint).
Wang, C.-C. & Truesdell, C. (1973). Introduction to Rational Elasticity. Noordhoff.
Valent, T. (1988). Boundary-Value Problems of Finite Elasticity Springer-Verlag.
Fu, Y.B. & Ogden, R.W. (2001). Nonlinear Elasticity. Eds., Cambridge.
Drozdov, A.D. (1996). Finite Elasticity and Viscoelasticity. World Scientific.
Atkin, R.J. & Fox, N. (1980). An Introduction to the Theory of Elasticity. Longman.
Evaluación
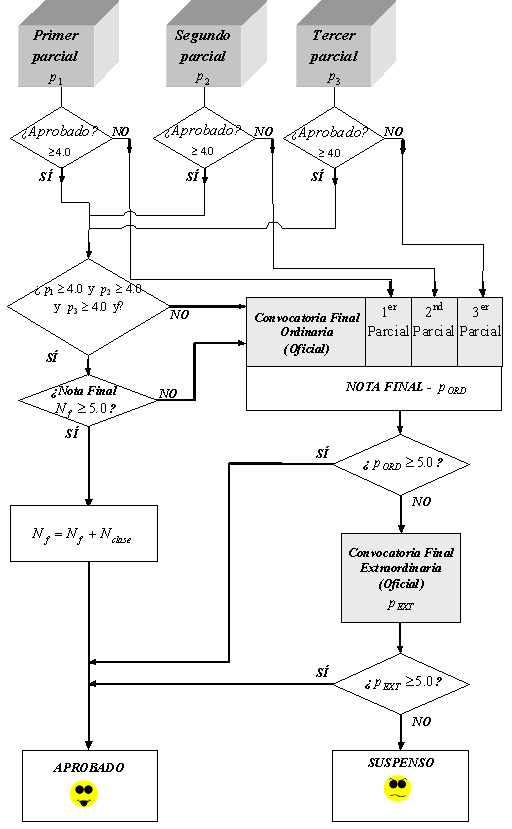
Las oportunidades de evaluación a lo largo del curso serán tres, dos de las cuales tendrán el carácter de exámenes finales y la tercera el de evaluación por curso.
Los exámenes finales consistirán en una prueba única que abarcará toda la materia impartida; se evaluarán de 0 a 10 puntos, siendo necesario alcanzar una nota igual o superior a 5 puntos para superar la asignatura. En el examen final de la convocatoria ordinaria los alumnos pueden optar por examinarse sólo de aquellas partes que tengan suspensas. En el examen final de la convocatoria extraordinaria los alumnos se examinarán de toda la materia impartida.
La evaluación por curso consta de 5 notas. Las tres primeras corresponden a tres pruebas escritas excluyentes, puntuadas de 0 a 10 puntos, siendo necesario alcanzar un mínimo de 4,0 en cada una de ellas para poder superar la asignatura por curso. La cuarta nota corresponde a la actividad desarrollada por el alumno en clase y será evaluada por el profesor de 0 a 2 puntos. La quinta nota corresponde a las entregas de ejercicios a lo largo del curso, y será evaluada por el profesor de 0 a 1 puntos. La asignatura se habrá superado por curso cuando la suma de las cinco notas sea igual o superior a 15 puntos, cumpliendo los mínimos de puntuación indicados para las pruebas escritas. Las notas de las pruebas escritas iguales o superiores a 4,0 puntos se conservan en el examen final de la convocatoria ordinaria, sin perjuicio de que el alumno pueda presentarse para mejorar nota.
Apuntes
CHAVES, E.W.V.(2012-3ª Edición). “Mecánica del Medio Continuo. Conceptos Básicos”. CIMNE-Barcelona, ISBN: 978-84-96736-38-2.(1ªEdición: 2007, 2ªEdición: 2010).
Introducción;
1 Tensores; Apéndicie A; 2 Cinemática del Continuo;
3 Tensiones;
4 Objetividad de Tensores;
5 Ecuaciones Fundamentales de la Mecánica del Medio Continuo;
6 Introducción a las Ecuaciones Constitutivas;
7 Elasticidad Lineal.
CHAVES, E.W.V. (2009). “Mecánica del Medio Continuo. Modelos Constitutivos”. CIMNE, ISBN: 978-84-96736-68-9.
Introducción;
1 Hiperelasticidad;
2 Plasticidad;
3 Termoelasticidad. Termoplasticidad;
4 Fluidos;
5 Viscoelasticidad;
6 Mecánica del Daño.
CHAVES, E.W.V. “Mecánica del Medio Continuo: Problemas Resueltos”. CIMNE-Barcelona, ISBN: 978-84-943307-5-9.(1ªEdición: 2014).
1 Tensores;
2 Cinemática del Continuo;
3 Tensiones;
Ecuaciones Fundamentales de la mecánica del Medio Continuo;
5 Introducción a las ecuaciones Constitutivas;
6 Elasticidad Lineal ;
Links
UPC-Prof. Oliver (Mecánica de Medios Continuos)
Continuum Mechanics School of Engineering-Brown University
MITOPENCOURSEWARE (Computational Science and Engineering)
You Tube
Eulerian and Lagrangian Description
2. Deformation of Continuous Media
MIT-Finite Element Procedures for Solids and Structures, Nonlinear Analysis(Prof. Klaus-Jürgen Bathe)
Lecture 1 Lecture 2 Lecture 3 Lecture 4 Lecture 5 Lecture 6 Lecture 7
[/vc_column_text][/vc_tta_section][/vc_tta_accordion][/vc_column][/vc_row][vc_row][vc_column][vc_column_text]
Contenido de la Asignatura
I.A Tensores
El espacio de los tensores geométricos. Suma de tensores geométricos. Producto de tensor por escalar. Producto tensorial de vectores geométricos. Producto de tensores geométricos. Determinante de un tensor geométrico. Traza de un tensor geométrico. Autovalores y autovectores de un tensor. Trasposición de tensores geométricos. Producto escalar de tensores geométricos. Tensores geométricos simétricos. Tensores geométricos hemisimétricos. Tensores geométricos ortogonales. Descomposición de tensores geométricos.
I.B Teoría de Campos
Campos escalares, vectoriales y tensoriales. Operadores diferenciales. Propiedades de los operadores diferenciales. Operadores diferenciales compuestos. Transformaciones integrales. Coordenadas cartesianas. Coordenadas cilíndricas.
BLOQUE II: INTRODUCCIÓN A LA MECÁNICA DE MEDIOS CONTINUOS
II.A Cinemática y Dinámica de Medios Continuos
El medio continuo como sistema mecánico: Materiales y medios continuos. Conservación de la masa. Fuerzas interiores. El vector tensión.
Cinemática de Medios Continuos: Descripciones del movimiento. Pequeñas deformaciones. Deformaciones longitudinales y angulares. Deformaciones y desplazamientos. Tensor de pequeñas deformaciones. Campo de deformaciones.
Dinámica de Medios Continuos: El tensor de tensiones. Teoremas de conservación. Tensiones estáticamente determinadas.
Termodinámica de medios continuos: Calor y temperatura en un medio continuo. El vector de flujo térmico. Primer principio. Segundo principio.II.B Ecuaciones Constitutivas de Sólidos y de Fluidos.
Postulados fundamentales: Determinismo. Axioma de acción local. Objetividad. Disipación universal.
Ecuaciones constitutivas de sólidos: Elasticidad clásica. El material hookeano.
Ecuaciones constitutivas de fluidos: Concepto de presión (hidrostática, media y termodinámica). Fluido newtoniano isótropo.