Anuncio
Prácticas-Placa adicional (Actualización:21/11/2011)
Organización
Clases:
Lunes, 12:00h – 14:30h
Martes, 8:30h – 10:00h
Jueves, 13:00h – 14:30h
Viernes, 11:30h – 13:00h
Gonzalo Ruiz:
Rena Yu:
Eduardo W.V. Chaves: Cualquier hora
Referencias
VALIENTE, A. (2000), Curso de Comportamiento Mecánico de Materiales, Elasticidad y Viscoelasticidad. Servicio de Publicaciones de la E.T.S. de Ingenieros de Caminos, C. y P. de la Universidad Politécnica de Madrid, Madrid.
OLIVER, X. & AGELET DE SARACÍBAR, C. (2000). Mecánica de Medios Continuos para Ingenieros. Edicions de la Universitat Politècnica de Catalunya, Barcelona.
SÁNCHEZ GÁLVEZ, V. (1999). Curso de Comportamiento Plástico de Materiales. Servicio de Publicaciones de la E.T.S. de Ingenieros de Caminos, C. y P. de la Universidad Politécnica de Madrid, Madrid.
ELICES, M. (2000). Mecánica de la Fractura Aplicada a Sólidos Elásticos Bidimensionales. Servicio de Publicaciones de la E.T.S. de Ingenieros de Caminos, C. y P. de la Universidad Politécnica de Madrid, Madrid.
CALLISTER, W.D. (1995). Introducción a la Ciencia e Ingeniería de los Materiales. Reverté, Barcelona.
MIRAVETE, A. (2000). Materiales Compuestos. Servicio de Publicaciones de la Universidad de Zaragoza (Centro Politécnico Superior), Zaragoza.
CHAVES, E.W.V. (2007). “Mecánica del Medio Continuo. Conceptos Básicos“. Centro Internacional de Métodos Numéricos en Ingeniería (CIMNE), Barcelona, ISBN: 978-84-96736-38-2.
CHAVES, E.W.V. (2009). “Mecánica del Medio Continuo: Modelos Constitutivos“. Centro Internacional de Métodos Numéricos en Ingeniería (CIMNE), Barcelona, ISBN: 978-84-96736-68-9.
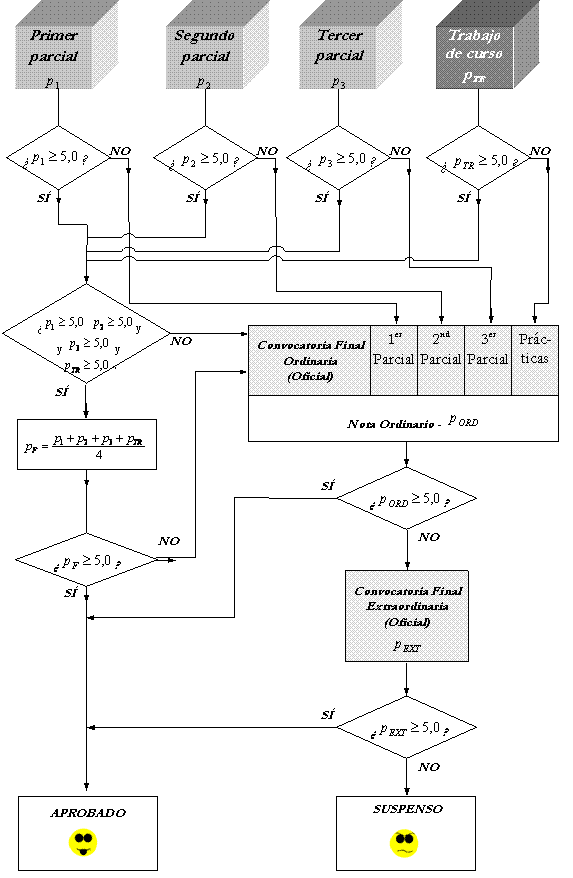
Evaluación
Las oportunidades de evaluación a lo largo del curso serán tres, dos de las cuales tendrán el carácter de exámenes finales y la tercera el de evaluación por curso.
Los exámenes finales consistirán en una prueba única que abarcará toda la materia impartida; se evaluarán de 0 a 10 puntos, siendo necesario alcanzar una nota igual o superior a 5 puntos para superar la asignatura. En el examen final de la convocatoria ordinaria los alumnos pueden optar por examinarse sólo de aquellas partes que tengan suspensas. En el examen final de la convocatoria extraordinaria los alumnos se examinarán de toda la materia impartida.La evaluación por curso consta de 6 notas. Las tres primeras corresponden a tres pruebas escritas excluyentes, puntuadas de 0 a 10 puntos, siendo necesario alcanzar un mínimo de 5,0 en cada una de ellas para poder superar la asignatura por curso. La cuarta nota corresponde a la nota de prácticas de laboratorio, puntuada de 0 a 10 puntos, siendo necesario obtener 5 o más puntos para poder superar la asignatura por curso. La quinta nota corresponde a la actividad desarrollada por el alumno en clase y será evaluada por el profesor de 0 a 1 puntos. La sexta nota corresponde a las entregas de ejercicios a lo largo del curso, y será evaluada por el profesor de 0 a 2 puntos. La asignatura se habrá superado por curso cuando la suma de las seis notas sea igual o superior a 20 puntos, cumpliendo los mínimos de puntuación indicados para las pruebas escritas y la evaluación de prácticas. Las notas de las pruebas escritas iguales o superiores a 3.5 puntos se conservan en el examen final de la convocatoria ordinaria, sin perjuicio de que el alumno pueda presentarse para mejorar nota.
Ejercicio y prácticas
]Curso 2011-2012
Relación de Grupos y Fechas de Ensayo de Laboratorio
Presentación de Introducción a Elementos Finitos
Presentación de Introducción a Elementos Finitos
Objetivos
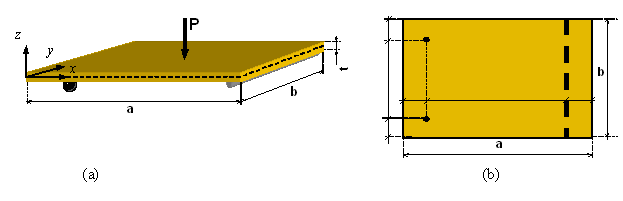
Determinación analítica, numérica y experimental de la línea de rotura en el ensayo de una placa rectangular Figura 1(a) solicitada por una carga puntual en su centro geométrico, y apoyada de forma continua en un lado y de forma puntual en el otro lado como indicado en la Figura 1(b)
&nb>Presentación de Introducción a Elementos Finitos
Presentación de Introducción a Elementos Finitos
Objetivos
Determinación analítica, numérica y experimental de la línea de rotura en el ensayo de una placa rectangular Figura 1(a) solicitada por una carga puntual en su centro geométrico, y apoyada de forma continua en un lado y de forma puntual en el otro lado como indicado en la Figura 1(b)
Descripción de la práctica
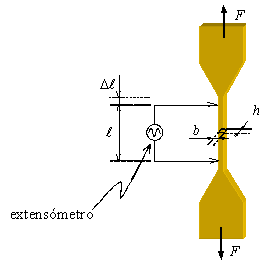
Con un ensayo de tracción se obtienen la curva s-e y las propiedades mecánicas del material con que se han fabricado las placas (latón, material compuesto por cobre y zinc). Se utiliza una probeta con forma de hueso, con una sección de , ver Figura 2. El coeficiente de Poisson del latón es 0.35.
Se ensayan dos placas rectangulares de las siguientes dimensiones: la placa 1 mide (ancho largo espesor), y la placa 2, , (dimensiones a medir en laboratorio). Las placas se apoyan en un dispositivo de flexión compuesto por un bastidor rígido sobre el que se montan los soportes a la distancia deseada. En el ensayo se miden la carga aplicada, P, y el desplazamiento bajo el punto de carga, d.
Asimismo, se realizan cálculos de la geometría ensayada utilizando dos procedimientos: el método analítico de las líneas de rotura; y el programa comercial de elementos finitos ANSYS.
1. Medir las dimensiones de la geometría de las probetas.
2. Realizar el ensayo de tracción. Realizar el ensayo de rotura de placas.
3. Realizar un informe en el que figure:
· Descripción del ensayo, tablas de datos tomados en laboratorio, incidencias.
· Análisis de los resultados: gráfico de las curvas s-e y P-d. Estudio de la influencia de la geometría en las curvas P-d y en los mecanismos de rotura.
· Aplicación de la teoría simplificada de cálculo de placas en estado límite a las placas ensayadas. Estudio analítico de la transición entre los posibles mecanismos de rotura. Comparación entre los valores de carga máxima teóricos y los experimentales.
· Estudio numérico de los dos casos ensayados utilizando el programa ANSYS. Gráfico de las curvas P-d numéricas comparadas con las correspondientes curvas experimentales.
· Estudio comparativo del colapso de la placa propuesta a cada grupo por ambos métodos (líneas de rotura y ANSYS).
Download: Practica.pdf
Introducción al ANSYS sp;
Descripción de la práctica
Con un ensayo de tracción se obtienen la curva s-e y las propiedades mecánicas del material con que se han fabricado las placas (latón, material compuesto por cobre y zinc). Se utiliza una probeta con forma de hueso, con una sección de , ver Figura 2. El coeficiente de Poisson del latón es 0.35.
Se ensayan dos placas rectangulares de las siguientes dimensiones: la placa 1 mide (ancho largo espesor), y la placa 2, , (dimensiones a medir en laboratorio). Las placas se apoyan en un dispositivo de flexión compuesto por un bastidor rígido sobre el que se montan los soportes a la distancia deseada. En el ensayo se miden la carga aplicada, P, y el desplazamiento bajo el punto de carga, d.
Asimismo, se realizan cálculos de la geometría ensayada utilizando dos procedimientos: el método analítico de las líneas de rotura; y el programa comercial de elementos finitos ANSYS.
1. Medir las dimensiones de la geometría de las probetas.
2. Realizar el ensayo de tracción. Realizar el ensayo de rotura de placas.
3. Realizar un informe en el que figure:
· Descripción del ensayo, tablas de datos tomados en laboratorio, incidencias.
· Análisis de los resultados: gráfico de las curvas s-e y P-d. Estudio de la influencia de la geometría en las curvas P-d y en los mecanismos de rotura.
· Aplicación de la teoría simplificada de cálculo de placas en estado límite a las placas ensayadas. Estudio analítico de la transición entre los posibles mecanismos de rotura. Comparación entre los valores de carga máxima teóricos y los experimentales.
· Estudio numérico de los dos casos ensayados utilizando el programa ANSYS. Gráfico de las curvas P-d numéricas comparadas con las correspondientes curvas experimentales.
· Estudio comparativo del colapso de la placa propuesta a cada grupo por ambos métodos (líneas de rotura y ANSYS).
Download: Practica.pdf
Introducción al ANSYS
Apuntes
Presentación de Introducción a Elementos Finitos
Presentación de Introducción a Elementos Finitos
Download: Practica.pdf
Método Analítico
OBJETIVOS
Los objetivos cognoscitivos de la “Mecánica de Medios Continuos y Ciencia de Materiales” están descritos por el Plan de Estudios de la Escuela de Caminos, y so: “Ecuaciones Constitutivas, Elasticidad y Viscoelasticidad, Plasticidad y Viscoplasticidad, Mecánica de la Fractura, Ciencia de Materiales”. Como se ve a través de los descriptores, la asignatura aborda la Mecánica de Sólidos basándose en la Ciencia de Materiales y centrándose en el comportamiento de los materiales de interés en ingeniería civil. Es continuación natural de “Física I” y de “Ampliación de Mecánica”. Asimismo, amplia y desarrolla conceptos de “Ciencia y Tecnología de Materiales”.
CONTENIDO DE LA ASIGNATURA
Bloque I: Elasticidad y Viscoelasticidad
I.A Comportamiento elástico
Micromecánica del comportamiento elástico. Elasticidad clásica: el material hookeano. Energía elástica. El problema elástico. Elproblema elástico en el plano. Termoelasticidad. El problema termoelástico. Materiales elástico-lineales anisótropos. Materiales elástico-lineales ortótropos y tranversalmente isótropos. Elasticidad no lineal.
I.B Comportamiento viscoelástico
Viscoelasticidad lineal: el material de Boltzmann. Ecuaciones constitutivas del material de Boltzmann. Modelos mecánicos. El problema viscoelástico.
Bloque II: Plasticidad y Viscoplasticidad
II.A Comportamiento plástico
Introducción al comportamiento plástico. Criterios de plastificación. Ecuaciones constitutivas de la Plasticidad. Teoremas generales. El problema plástico. Deformación plana. Líneas de deslizamiento. Plastificación de vigas y pórticos. Plastificación de placas. Plastificación de tubos. Teoría de dislocaciones. Endurecimiento de metales y aleaciones.
II.B Comportamiento viscoplástico
Viscoplasticidad. Fluencia y relajación.
Bloque III: Mecánica de la Fractura
III.A Criterios de rotura: planteamiento global
Planteamiento global. Funciones G y R. Cálculo de la energía disponible para la fractura G. Medida de la resistencia a la fractura R.
III.B Criterios de rotura: planteamiento local
Planteamiento local. Funciones K y Kc. Cálculo del factor de intensidad de tensiones K. Medida de la tenacidad de fractura KIc.
III.C Fisuras subcríticas
Crecimiento de fisuras por fatiga. Fatiga con amplitud de carga constante. Fatiga con amplitud de carga variable. Crecimiento de fisuras por corrosión bajo tensión. Crecimiento de fisuras por corrosión-fatiga. Crecimiento de fisuras por fluencia.
Bloque IV: Materiales Compuestos
Introducción a los materiales compuestos. Propiedades de los materiales compuestos. Criterios de rotura de materiales compuestos.
Prácticas de laboratorio
Práctica 1: Influencia de la velocidad de solicitación en un ensayo de tracción directa.
Práctica 2: Ensayo de plastificación de placas.
Práctica 3: Medida de la energía específica de fractura R.
Práctica 4: Simulación del comportamiento mecánico de sólidos mediante el Método de los Elementos Finitos.